Графическая последовательность

Степенные последовательности

Эта глава посвящена теории степенных последова-тельностей. Напомним, что степенной последователь-ностью графа называется список степеней его вершин.

Часто по степеням вершин графа можно судить о его строении. Например, граф, в котором полусумма сте-пеней вершин (т. е. число ребер) не меньше числа вер-шин, содержит цикл (следствие 13.6); граф, степень каждой вершины которого равна двум, есть дизъюнкт-ное объединение циклов; граф, степень каждой вершины которого - четное число, не равное нулю, является объ-единением циклов (теорема 43.1) и т. д. В предыдущих главах есть и другие факты, поддающиеся интерпрета-ции подобного рода.

Естественно возникают следующие вопросы. Как свя-заны между собой степени вершин графа? Как по списку степеней вершин судить о свойствах графа? Какова связь между графами с совпадающими списками сте-пеней вершин? Можно ли построить граф с заданным списком степеней вершин и предписанными теоретико-графовыми свойствами и как это сделать?

Подобные вопросы особенно интенсивно изучаются в настоящее время. Это не только продиктовано внутрен-ней логикой развития теории графов, но имеет и прак-тическое значение. Если в виде графа представляется коммуникационная схема, узлам которой соответствуют вершины графа, а ребрам - каналы связей между вер-шинами, то возникает задача построения графа с задан-ными степенями вершин и, например, максимально воз-можной связностью. Такой граф соответствовал бы схеме

с заданными пропускными способностями узлов и мак-мамальной надежностью. Одна из исторически первых задач теории графов также относится к этому кругу проблем. Именно, в 1857 году А. Кэли, изучая насыщен-ные углеводороды, пришел к задаче перечисления де-ревьев, степени вершин которых равны 1 и 4.

Графическая последовательность

Последовательность (d₁, d₂, .., d_n) целых неотрица­тельных чисел ниже называется п-последователъностъю и обозначается одной буквой d. n-последовательность d на-зывается графической, если существует граф, степенная последовательность которого совпадает с d Этот граф называется реализацией последовательности d.

Очевидно, что порядок членов в графической n-после-довательности d несуществен, а каждый ее член d_i удов­летворяет неравенствам 0<d_t<п-1. Часто удобно эти последовательности считать невозрастающими. Согласно лемме о рукопожатиях сумма всех членов графической последовательности является четным числом.

Назовем n-последовательность d правильной, если вы-полняются два следующих условия:

1) n-l>d_l>d₂>...>d_n,

П

2) 2j di— четное число.

i=l

Без ограничения общности графическую последова­тельность можно считать правильной.

Иногда последовательность d удобно записывать в ви­де d = (c₁^k1, c₂^k2 ,..., с_р^kp), где числа c_i, попарно различны, а показатель k_i означает количество повторений числа с_i в последовательности d. Так, (5, 2, 1⁶) = (5, 2, 1, 1, 1, 1, 1, 1).

Рассмотрим последовательность d=(2⁴,1⁴).Существуют ровно пять графов, являющихся реализациями последовательности d. Они имеют следующие компонен-ты: 1) С₄, К₂ и К₂,2) К₃ ,P₃ и К₂ ,3) P₆ и К₂ ,4) P₅ и P₃ ,5) Р₄и Р₄.

В общем случае графическая последовательность име­ет много реализаций и их число определить сложно. В установлении связи между этими реализациями важ­ную роль играет вводимое ниже понятие переключения. Пусть G - граф, а,b,с,d - четыре его попарно различные вершины, причем ab € EG ,cd € EG, но ac¢EG, bd ¢ EG. Тогда говорят, что граф G допускает переключение s=(ab, cd). Полученный в результате переключения s граф обозначается через sG ;граф G превращается в sG в результате удаления ребер аb и cd и присоединения ребер ас и bd: sG = G - ab - cd + ac + bd. Обратное переключение s^-1=(ac, bd) применимо к графу sG.

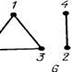
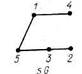
Тождественное преобразование ребер графа также по определению является переключением. Например, на рис. 45.1 изображены графы G и sG, ({1, 3} ,{4, 2}).

Очевидно, что переключение не меняет степеней вершин графа. Роль переключений определяется следующей теоремой.

Теорема 45.1. Любая реализация графической последовательности получается из любой другой ее реализации посредством применения подходящей цепочки переключений.

Доказательство этой теоремы основано на следующей лемме.

Рис. 45.1

Лемма 45.2. Пусть G - граф, вершины которого пронумерованы числами 1, 2, ..., п в порядке невозраста-ния степеней: G = {1, 2, ..., n}, deg i = d_i d_t> d_i+1 , i = 1, n - 1.когда для любой его вершины i существует такая последовательность переключений s₁ , ..., s_t , что в графе Н = s_t...s₁G окружение вершины i совпадает с множе-ством из d_i вершин наибольших степеней, т. е.

{1,2, . ..,d_i}, если i>d_{i ,}

({1,2,...,i - 1, i + 1, ...,d_i+1}, если i<d_i.

Пусть i,j,k € VG, j > k , ij € EG, ik ¢ EG. Так как >dj, то существует четвертая вершина l, смежная с k , 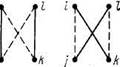не смежная с j (рис. 45.2, где, как и всюду в этой главе, пунктирными линиями обозначены ребра, отсутствующие в
графе). Следовательно, граф G допускает переключение s=(ij, kl).
Если G'=sG, то ik € EG', ij € EG'. Сделав несколько подобных переключений, придем к нужному графу Н.

Доказательство теоремы 45.1. Пусть d — правильнаяя графическая n -последовательность.Воспользуемся индукцией по п. Как подтверждает прямая проверка,
при n ≤ 4 каждая графическая последовательность имеет только одну реализацию. Следовательно, для п≤ 4 утверждение теоремы тривиально. Пусть п>4 и это утверждение верно для всех графических (п - 4)-последовательностей. Пусть, далее, G₁ и G₂ – две реализации последовательности d. Для каждого из графов G₁ и G₂ обозначим через v какую-либо вершину степени d₁ . Согласно лемме 45.2 существуют такие цепочки переключений s₁,..., s_t и s₁ ,..., s_r , что в графах H₁ = s_t... s₁G₁ и H₂= s_r....s₁G₂ окружения вершины v состоят из вершин степеней d₂ ,d₃ ,...,d_d1+1. Поэтому степенные последовательности графов H₁ - v и H₂ - v совпадают. По индуктивному предположению существует такая цепочка переключений s₁ , ..., s_h, что

H₁ - v =s_k , ...,s₁ (H₂ - v).

Эти переключения не затрагивают вершины v, поэтому H₁ = s_k , ...,s₁H₂. Далее имеем

G₁ = s₁^-1... s_t^-1H₁ = s₁^-1... s_t^-1s_k.... s₁H₂ = s₁^-1... s_t^-1s_k ....s₁s_t^' ...s₁^'HG₃.

Иногда, хотя и редко, граф определяется своей сте­пенной последовательностью однозначно. Если все реа­лизации графической последовательности изоморфны, то эта последовательность называется униграфической, а ее реализация — униграфом. Строение униграфов из­вестно, однако его описание слишком сложно. Унигра­фом является, например, простой цикл C₅.