Полосы равной толщины и равного наклона.
Классическим примером полос равной толщины являются кольца Ньютона. Они наблюдаются при отражении света от верхней и нижней границ тонкой воздушной прослойки, образованной поверхностями, соприкасающихся друг с другом толстой плоскопараллельной стеклянной пластинки и плосковыпуклой линзы с большим радиусом кривизны (рис. 32.4).
Большой радиус кривизны линзы делает поверхности пластинки и линзы,
обращенные друг к другу практически параллельными. Тем более, что
 | |||
 |
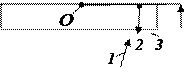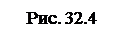являются когерентными при малой толщине прослойки h (длина когерентности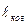 
должна быть больше 2h), поэтому при их сложении будет иметь место интерференция. Поскольку интерференция наблюдается в малой области вблизи точки касания О линзы и плоской стеклянной пластинки, поверхности линзы и пластинки здесь можно считать параллельными, а падающий и отраженный лучи (1, 2, 3) направленными вдоль одной прямой.
На радиусе r вдоль окружности толщина прослойки h будет одинаковой, и в этом случае наблюдаются интерференционные полосы равной толщины, имеющие форму колец с центром в точке касания линзы О. Эта интерференционная картина была впервые описана в 1675 г. Ньютоном и называется кольцами Ньютона.
Из рисунка 32.4 видно, что оптическая разность хода интерферирующих волн 2 и 3 Δ = 2hn +λ /2.
Коэффициент преломления воздуха n = 1. Слагаемое λ /2 возникает из-за того, что при отражении от оптически более плотной среды волны 3 (от стекла) оптический ход волны скачком увеличивается на λ /2. В том месте воздушного зазора, где выполняется условие
Δ = 2d + λ /2 = mλ (условие максимума),
наблюдаются светлые кольца, а там, где
Δ = 2d + λ /2 = (2m + 1) λ /2 (условие минимума),
возникают темные кольца. В месте соприкосновения линзы с плоскостью
 | |||
 | |||
вид концентрических колец. Таким образом, полосы равной толщины – это интерференционные полосы, возникающие в результате интерференции когерентных волн от мест с одинаковой толщиной.
Полосы равного наклона – интерференционные полосы, возникающие в результате наложения лучей, падающих на плоскопараллельную пластинку под одинаковыми углами.
Рассмотрим оптическую схему на рис. 32.6. Почти монохроматический
 |  | ||
задней поверхности пластины, снова преломляясь, попадает на экран (2-2΄). Если длина когерентности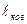 
>>2hn, где h – толщина пластины, а n – показатель преломления, то волны пучка, сходящиеся в некоторой точке экрана. например т. А, будут интерферировать. На схеме рис. 32.6 это волны, соответствующие лучам 1 и 2. Поскольку расходящийся от линзы пучок является коническим, то интерференционные полосы будут иметь вид окружностей. А так как интерференционные максимумы (а также минимумы) будут располагаться в местах, соответствующих одинаковому углу падения лучей (одинаковому наклону их к поверхности), то получающаяся картина называется полосами равного наклона.
Вопросы для самоконтроля.
1. В чем состоит явление интерференции?
2. Что такое когерентность?
3. В чем состоит временная когерентность?
Каков смысл времени и длины когерентности?
4. В чем состоит пространственная когерентность?
Каков смысл радиуса когерентности?
5. Что называется оптической длиной пути
и оптической разностью хода?
6. Каковы условия получения интерференционных максимумов и мини-
мумов при положении света от двух когерентных источников?
7. Как получаются полосы равной толщины и равного наклона?
Лекция № 33
ДИФРАКЦИЯ СВЕТА
План
1. Дифракция света. Принцип Гюйгенса-Френеля. Дифракция Френеля и Фраунгофера. Метод зон Френеля. Прямолинейное распространение света. Дифракция Френеля на круглом отверстии и диске.
2. Дифракция Фраунгофера на одной щели.
3. Дифракция Фраунгофера на одномерной дифракционной решетке. Многолучевая интерференция*.
4. Понятие о голографии.
Дата добавления: 2019-04-03; просмотров: 745;