Математическое моделирование пластовых систем.
Основная цель моделирования нефтяного пласта - описание его состояния с помощью соответствующих математических уравнений.
При моделировании пласта можно достаточно детально представить пласт путем разбиения его на блоки (иногда на несколько тысяч) и применения к каждому из них основных уравнений фильтрации.
В настоящее время используются программы для моделирования некоторых очень сложных процессов, протекающих при осуществлении различных вариантов разработки.
Для обозначения таких программ используют следующие равноценные термины: математические модели, численные модели, сеточные модели, конечно – разностные модели и далее пластовые модели.
В действительности в процессе разработки программы для моделирования пласта применяют три вида моделей:
1. Математическая модель.
Моделируемая физическая система описывается соответственно математическим уравнениями. Математические модели составляют на основе системы нелинейных дифференциальных уравнений в частных производных с соответствующими начальными и граничными условиями.
2. Численная модель.
Уравнения, описывающие математическую модель пласта, почти всегда настолько сложны что их невозможно решить аналитическими методами. Чтобы представить уравнения в форме, пригодной для решения на цифровых вычислительных машинах, следует их аппроксимировать, т.е. заменить исходные дифференциальные уравнения системой алгебраических уравнений. Численная модель состоит из полученной системы уравнений.
3. Машинная модель – это программа или система программ для ЭВМ, составленная с целью решения уравнений численной модели. Так математическая модель может отражать только те явления, которые были учтены при выводе дифференцируемых уравнений. Для конкретных месторождений эта информация часто является неполной. С помощью программ, базирующихся на данной конкретной модели, решается ряд дополнительных задач – например – изменение режима залежи, явления тепломассопереноса при закачке термоагентов и др.
Математическая постановка задач и их численное решение зависит от типа физической системы и допущений, принятых при разработке ее математической модели.
Различные формы уравнений (линейной, одномерной, однофазной) фильтрации можно подразделить:
1. Задачи стационарной линейной фильтрации, описываемые линейными обыкновенные дифференциальными уравнениями:
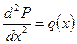
2. Задачи нестационарной линейной фильтрации, описываемые линейными дифференциальными уравнениями в частных производных:
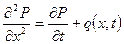
3. Задачи нестационарной линейной фильтрации, описываемые нелинейными дифференциальными уравнениями в частных производных с переменными коэффициентами:
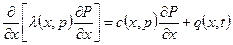
Моделирование многофазной фильтрации по сравнению с однофазным течением требует специальных методов решения, т.к. рассматривается система связанных нелинейных уравнений. Здесь используется метод аппроксимации, т.е. замена исходной задачи другой, более легкой, решение которой близко к решению исходной задачи. Одним из таких методов применяемых для решения математических задач разработки нефтяных месторождений является метод конечно – разностных аппроксимаций.
Сущность конечно – разностного метода заключается в замене исходных дифференцируемых уравнений системой алгебраических уравнений. Если полученная система линейная, то для ее решения применяют прямые и итерационные методы (к прямым методам относят метод Гаусса и его модификации; к итерационным – например метод Ньютона).
Если имеем дифференцируемое уравнение для искомой функции U, которая зависит от пространственной переменной X и времени t , то можно считать, что значения независимых переменных находятся на некоторой плоскости x,t.
При использовании конечно – разностных методов производят дискретизацию, т.е. замену непрерывных переменных x и t упорядоченной системой точек (узлов) на плоскости x,t со значениями по оси абсцисс xi и по оси ординат tn (i = 0, 1, 2,3….); n =( 0, 1, 2,3….N).
Геометрически дискретизацию можно интерпретировать как разделение плоскости x, t прямыми; параллельными осями x и t, т.е. нанесением на плоскость x,t сетки, узлы которой имеют координаты xi, tn.
Прямоугольник с координатами xi, xi +1, tn, tn +1 конечно – разностной ячейкой. Совокупность узлов xi (i = 0, 1, 2….I) при фиксированном tn, т.е. узлов, лежащих на прямых, параллельных оси x, называемой временным слоем.

Функция U теперь будет определена в узлах и обозначаться как: 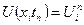
Разности xi +1 - xi = Δ xi +1 и tn +1 - tn = Δ tn +1 называются соответственно шагами по пространству и времени.

Если Δx = const или Δt = const, то сетка по пространству или по времени равномерная.
Для аппроксимации первой производной функции U по времени в узле i на n – ом временном слое имеем:
Δt – шаг по времени 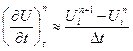
Аналогично аппроксимируется и первая производная функция U по пространству, например:
h – шаг по координате 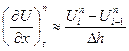
Интеграл ошибок или интеграл вероятности ошибок.



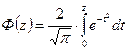
Используют явные и неявные конечно – разностные схемы.
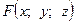
Конечно – разностные схемы лежат в основе решения системы дифференциальных уравнений при построении трехмерных, трехфазных математических моделей нефтяных пластов.

ЛЕКЦИЯ
Дата добавления: 2019-04-03; просмотров: 1114;
