Системы координат, применяемые в геодезии
Для определения положения точек в геодезии применяют пространственные прямоугольные, геодезические и плоские прямоугольные координаты.
Пространственные прямоугольные координаты. Начало системы координат расположено в центре O земного эллипсоида (рис. 2.2).
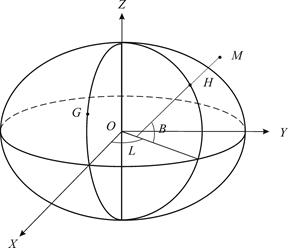
| Рис. 2.2. Земной эллипсоид и координаты: Х, Y , Z – пространственные прямоугольные; B, L, H - геодезические; G - Гринвич |
Ось Z направлена по оси вращения эллипсоида к северу. Ось Х лежит в пересечении плоскости экватора с начальным - гринвичским меридианом. Ось Y направлена перпендикулярно осям Z и X на восток.
Геодезические координаты. Геодезическими координатами точки являются ее широта, долгота и высота (рис. 2.2).
Геодезической широтой точки М называется угол В, образованный нормалью к поверхности эллипсоида, проходящей через данную точку, и плоскостью экватора.
Широта отсчитывается от экватора к северу и югу от 0° до 90° и называется северной или южной. Северную широту считают положительной, а южную - отрицательной.
Плоскости сечения эллипсоида, проходящие через ось OZ, называются геодезическими меридианами.
Геодезической долготой точки М называется двугранный угол L, образованный плоскостями начального (гринвичского) геодезического меридиана и геодезического меридиана данной точки.
Долготы отсчитывают от начального меридиана в пределах от 0° до 360° на восток, или от 0° до 180° на восток (положительные) и от 0° до 180° на запад (отрицательные).
Геодезической высотой точки М является ее высота Н над поверхностью земного эллипсоида.
Геодезические координаты с пространственными прямоугольными координатами связаны формулами
X = (N + H)cosB cosL,
Y = (N+H)cosB sinL,
Z = [(1 - e2) N+H] sinB,
где e - первый эксцентриситет меридианного эллипса и N -радиус кривизны первого вертикала.При этом N=a/(1 - e2 sin2B)1/2.
Геодезические и пространственные прямоугольные координаты точек определяют с помощью спутниковых измерений, а также путем их привязки геодезическими измерениями к точкам с известными координатами.
Отметим, что наряду с геодезическими существуют еще астрономические широта и долгота. Астрономическая широта j это - угол, составленный отвесной линией в данной точке с плоскостью экватора. Астрономическая долгота l – угол между плоскостями Гринвичского меридиана и проходящего через отвесную линию в данной точке астрономического меридиана. Астрономические координаты определяют на местности из астрономических наблюдений.
Астрономические координаты отличаются от геодезических потому, что направления отвесных линий не совпадают с направлениями нормалей к поверхности эллипсоида. Угол между направлением нормали к поверхности эллипсоида и отвесной линией в данной точке земной поверхности называется уклонением отвесной линии.
Обобщением геодезических и астрономических координат является термин – географические координаты.
Плоские прямоугольные координаты. Для решения задач инженерной геодезии от пространственных и геодезических координат переходят к более простым – плоским координатам, позволяющим изображать местность на плоскости и определять положение точек двумя координатами х и у.
Поскольку выпуклую поверхность Земли изобразить на плоскости без искажений нельзя, введение плоских координат возможно только на ограниченных участках, где искажения так малы, что ими можно пренебречь. В России принята система прямоугольных координат, основой которой является равноугольная поперечно–цилиндрическая проекция Гаусса. Поверхность эллипсоида изображается на плоскости по частям, называемым зонами. Зоны представляют собой сферические двуугольники, ограниченные меридианами, и простирающиеся от северного полюса до южного (рис. 2.3). Размер зоны по долготе равен 6°. Центральный меридиан каждой зоны называется осевым. Нумерация зон идет от Гринвича к востоку.
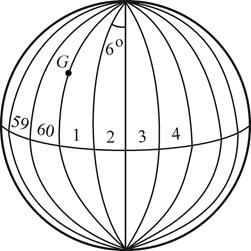
| Рис. 2.3. Деление поверхности Земли на координатные зоны: G – Гринвич |
Долгота осевого меридиана зоны с номером N равна:
l0 = 6°× N - 3° .
Осевой меридиан зоны и экватор изображаются на плоскости прямыми линиями (рис. 2.4). Осевой меридиан принимают за ось абсцисс x, а экватор - за ось ординат y. Их пересечение (точка O) служит началом координат данной зоны.
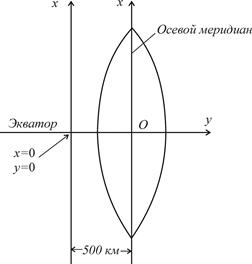
| Рис. 2.4. Изображение координатной зоны на плоскости: О – начало координат (х0=0; у0=500 км). |
Чтобы избежать отрицательных значений ординат, координаты пересечения принимают равными x0 = 0, y0 = 500 км, что равносильно смещению оси х к западу на 500 км.
Чтобы по прямоугольным координатам точки можно было судить, в какой зоне она расположена, к ординате y слева приписывают номер координатной зоны.
Пусть например, координаты точки А имеют вид:
xА = 6 276 427 м
yА = 12 428 566 м
Эти координаты указывают на то, что точка А находится на расстоянии 6276427 м от экватора, в западной части (y < 500 км) 12-ой координатной зоны, на расстоянии 500000 - 428566 = 71434 м от осевого меридиана.
Для пространственных прямоугольных, геодезических и плоских прямоугольных координат в России принята единая система координат СК-95, закрепленная на местности пунктами государственной геодезической сети и построенная по спутниковым и наземным измерениям по состоянию на эпоху 1995 г.
Местные системы прямоугольных координат.При строительстве различных объектовчасто используют местные (условные) системы координат, в которых направления осей и начало координат назначают, исходя из удобства их использования в ходе строительства и последующей эксплуатации объекта.
Так, при съемке железнодорожной станции ось у направляют по оси главного железнодорожного пути в направлении возрастания пикетажа, а ось х – по оси здания пассажирского вокзала.
При строительстве мостовых переходов ось х обычно совмещают с осью моста, а ось y идет в перпендикулярном направлении.
При строительстве крупных промышленных и гражданских объектов оси x и y направляют параллельно осям строящихся зданий.
Системы высот
Счет высот в инженерной геодезии ведут от одной из уровенных поверхностей.
Высотой точки называют расстояние по отвесной линии от точки до уровенной поверхности, принятой за начало счета высот.
Если высоты отсчитывают от основной уровенной поверхности, то есть от поверхности геоида, их называют абсолютными высотами. На рис. 2.5 отрезки отвесных линий Аа и Вв - абсолютные высоты точек А и В.
Если за начало счета высот выбрана какая-либо другая уровенная поверхность, то высоты называют условными. На рис. 2.5 отрезки отвесных линий Аа¢ и Вв¢ - условные высоты точек А и В.
В России принята Балтийская система высот. Счет абсолютных высот ведут от уровенной поверхности, проходящей через нуль Кронштадтского футштока.
Численное значение высоты принято называть отметкой. Например, если высота точки А равна HА = 15,378 м, то говорят, что отметка точки равна 15,378 м.
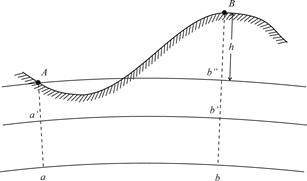
| Рис. 2.5. Абсолютные и условные высоты: a¢b¢ – уровенная поверхность; ab –поверхность геоида; Ab² – уровенная поверхность точки A; |
Разность высот двух точек называется превышением. Так, превышение точки В над точкой А равно
hAB = HВ - HA.
Зная высоту точки А, для определения высоты точки В на местности измеряют превышение hAB. Высоту точки В вычисляют по формуле
HВ = HA + hAB.
Измерение превышений и последующее вычисление высот точек называется нивелированием.
Абсолютную высоту точки следует отличать от ее геодезической высоты, то есть высоты, отсчитываемой от поверхности земного эллипсоида (см. раздел 2.2). Геодезическая высота отличается от абсолютной высоты на величину отклонения поверхности геоида от поверхности эллипсоида.
В заключение отметим, что точное определение положения поверхности геоида в области материков невозможно. Поэтому в России принято отсчитывать высоты от близкой к геоиду, но доступной точному определению вспомогательной поверхности, названной квазигеоидом. Высоты, отсчитываемые от поверхности геоида, называются ортометрическими высотами, а отсчитываемые от поверхности квазигеоида – нормальными высотами. На результаты измерений, выполняемых в инженерной геодезии, различия в двух названных системах высот влияния не оказывают, и в дальнейшем мы их различать не будем, а будем пользоваться введенным выше обобщенным понятием – абсолютные высоты.
Дата добавления: 2019-04-03; просмотров: 2267;
