ТЕРМОДИНАМИЧЕСКИЕ РАСЧЕТЫ В ТЕХНОЛОГИИ РЕДКИХ МЕТАЛЛОВ
Химическая термодинамика позволяет установить принципиальную осуществимость того или иного процесса, а также ответить на вопрос о более вероятной химической реакции из числа возможных в данной системе; позволяет рассчитать тепловой эффект реакции, что важно для аппаратурного оформления процесса, а также константу равновесия химической реакции и тем самым ответить на вопрос о степени превращения вещества в процессе химической реакции.
Термодинамический анализ дает возможность судить об оптимальной для выхода продукта температуре реакции. Направление химической реакции определяется знаком изменения изобарно-изотермического потенциала DG (энергии Гиббса) или изохорно-изотермического потенциала DА (энергии Гельмгольца), происходящего в системе в результате реакции.
Энергия Гиббса определяется уравнением
G = Н — TS = U — TS + pV, (1)
где Н—энтальпия; S—энтропия; U—внутренняя энергия; Т—температура; р—давление; V—объем.
В литературе в качестве синонимов для величины G употребляют термины «изобарно-изотермический потенциал», «свободная энтальпия», «свободная энергия при постоянном давлении» и «энергия Гиббса». В этой работе принят термин «энергия Гиббса», условное обозначение G (до 1961 г. эта величина в различных работах обозначалась Z и F).
Изменение энергии Гиббса DG является мерой химического сродства. Уменьшение ее выражает максимальную полезную работу процесса при постоянном давлении, т. е. равно максимальной работе реакции за вычетом работы против внешнего давления. При отрицательном значении DG реакция идет слева направо, при положительном имеет место обратная реакция, при значении DG = 0 наступает истинное химическое равновесие.
Процессы, протекающие при постоянных объеме и температуре, характеризуются изохорно-изотермическим потенциалом или энергией Гельмгольца А, которая определяется уравнением
А = U — TS. (2)
Если реакция протекает без изменения объема, DА = DG.
Константу равновесия химической реакции рассчитывают по изменению энергии Гиббса или Гельмгольца для веществ, взятых в стандартном состоянии, в соответствии с уравнениями:
DGo = - RTlnKp,T (3)
DAo = - RTlnKV,T (3)
где Кр - константа реакции при р = const; Kv—константа реакции при V=const; индекс o указывает на стандартное состояние. Для индивидуальных твердых и жидких веществ в качестве стандартного состояния принимают состояние их при данной температуре при давлении 1 атм. За стандартное состояние индивидуального газа принимается состояние гипотетического идеального газа, фугитивность которого равна единице при данной температуре. Свойства реальных газов при давлении 1 атм незначительно отличаются от свойств газов в стандартном состоянии, и при технологических расчетах этой разницей можно пренебречь. Рассматривая протекание газовой реакции в стандартных условиях, следует иметь в виду, что парциальное давление каждого из компонентов реакции равно 1 атм. Применительно к растворам в качестве стандартного состояния используют, как правило, либо стандартное состояние «чистого вещества», либо стандартное состояние гипотетического 1 М раствора со свойствами «бесконечно разбавленного» раствора.
Основные термодинамические свойства веществ в стандартном состоянии приведены в многочисленной справочной литературе.
Расчет DGo предполагает, таким образом, расчет для реакции гипотетической, никогда на практике не осуществимой. Так, для реакции
На (г.) + F2 (г.) = 2HF; DGo 298 = - 129,4 ккал.
Это означает, что образование двух молей фтористого водорода в очень большом количестве смеси, в которой парциальное давление pн2= рF2 = рНF = 1 атм при 298° К, приводит к уменьшению потенциала на 129,4 ккал. Для реакции
ТiO2 (тв.) + С (тв.) + 2С12(г.) = TiCI4(г.) + СО2 (г.)
такое уменьшение потенциала имеет место при невыполнимых практически условиях реакции, когда суммарное давление над твердыми ТiO2 и С равно 1 атм и в то же время парциальное давление pTiCI4 = рС12= рСО2 =1 атм.
Весьма полезным для термодинамических расчетов реакций с участием редких металлов является многотомное издание Я. И. Герасимова, А. Н. Крестовникова и А. С. Шахова «Химическая термодинамика в цветной металлургии», М., Металлургиздат, I960. Значения теплоты образования, энтропии, параметров фазового перехода, коэффициента температурной зависимости, теплоемкости, давления насыщенного пара и изменения энергии Гиббса при реакциях образования для большого числа редких элементов содержатся в справочнике «Термодинамические свойства неорганических веществ» (под ред. А. П. Зефирова. М., Атомиздат, 1965. Авт.: У. Д. Верятин, В. П. Маширев, Н. Г. Рябцев, В. И. Тарасов, Б. Д. Рогозкин, И. В. Коробов). Систематические данные по основным термодинамическим свойствам веществ публикуются в справочнике «Термодинамические константы веществ». (Вып. 6. Под ред. В. Н. Глушко и др. М., ВИНИТИ, 1965.)
Для химических реакций DGo = 0 или DGАo = 0 в общем случае не является критерием равновесия. Таким критерием является изменение DG в реальных условиях реакции. Для реакции aA + bB = cC + dD
DG = DGo – Rtln[AaBb/CcDd] (5)
Можно считать на основании анализа многочисленных данных, что химическая реакция осуществима, если значение DGo < - 10 ккал, и неосуществима при значениях DGo >10 ккал.
Для химической реакции в стандартных условиях при определенной температуре (обычно 25°С) DGo можно определить из справочных данных как алгебраическую сумму DGo298 образования веществ, принимающих участие в реакции. При вычислении константы равновесия при температуре, отличной от справочной, используют зависимость
DGoT = DHoT - DSoT (6)
Для некоторых процессов в литературе даются значения приведенного потенциала DФoT, определяемого по уравнению:
ФoT = - (GoT – HoT) / Т (7)
Константа равновесия реакции связана с приведенным потенциалом соотношением
RlnKp = DФoT = DHo0 / Т (8)
где DHo0 - изменение энтальпии в результате химической реакции при абсолютном нуле.
В некоторых случаях, когда для соединений редких металлов исходные данные для термодинамического расчета отсутствуют, приходится пользоваться различными методами расчета этих величин.
ЭНТАЛЬПИЯ
Кроме того, что энтальпия в значительной степени определяет термодинамический потенциал и тем самым направление процесса и константу равновесия, знание теплового эффекта реакции необходимо для рационального построения любого технологического процесса. Тепловой эффект исключительно важен при расчете теплового баланса процесса, особенно для определения возможности осуществления процесса в аппарате с подогревом или без него. Энтальпию можно вычислить на основании закона Гесса как алгебраическую сумму теплоты образования всех участников реакции. При отсутствии необходимых данных энтальпию можно рассчитать сравнительными методами. Так, по правилу термодинамической логарифмики, предложенному А. Ф. Капустинским:
DH/W = A lgZ + B
где W—валентность элемента в соединении; Z—порядковый номер элемента в периодической системе; А и В — константы. На рис. 7 приведен пример расчета энтальпии образования трихлорида ванадия no этому правилу.
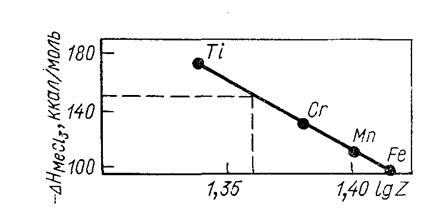
Рис. 7. Расчет энтальпии образования трихлорида ванадия по правилу термодинамической логарифмики -DHVCl3 = 150 ккал/моль.
Для расчета энтальпии можно использовать сравнительные методы М. X. Карапетьянца. Так, по первому методу, в основе которого лежит сравнение значений данного свойства в рядах других веществ, энтальпию вычисляют по уравнению:
DHII =A1DHI + B2,
где DHI и DHII - энтальпии образования в ряду сходных веществ; A1 и B2 - константы. На рис. 8 показан пример расчета по этому методу энтальпии образования трихлорида ванадия.
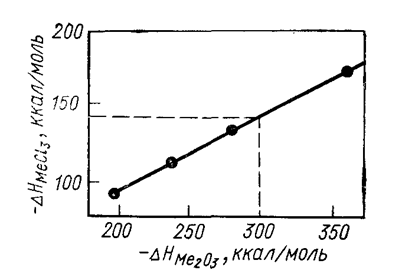
Рис. 8. Расчет энтальпии образования трихлорида ванадия по первому сравнительному методу М. X. Карапетьянца: -DHVCl3 = 142 ккал/моль.
По второму методу сравнительного расчета сравнивают значения двух свойств в одном ряду веществ. В. П. Шишокин связал изменение энтальпии DH с эквивалентным ионизационным потенциалом Iэкв.
Iэкв = (Iкат + Iан) / N,
где Iкат и Iан —первые ионизационные потенциалы катиона и аниона; N—номер группы периодической системы, к которой принадлежит металл. Аналитическим выражением данного метода является уравнение
DH = АÖIэкв + В,
где А и В — константы для данного ряда периодической системы. На рис. 9 показано определение энтальпии образования хлорида ванадия по этому методу.
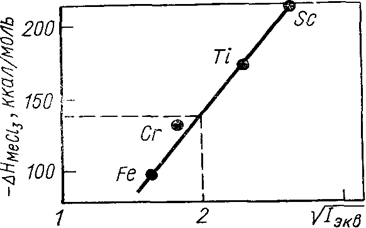
Рис. 9. Расчет энтальпии образования трихлорида ванадия по методу В. П. Шишокина: -DHVCl3 = 135 ккал/моль.
Л. П. Рузинов и др. предложили зависимость энтальпии хлоридов от суммы ионизационного потенциала (Ew) и теплоты сублимации металлов (HS), входящих в состав хлоридов:
DH = А(EW + HS) + B,
где А и В — константы. Расчет энтальпии по этому методу показан на рис. 10. Рассматривая полученные данные как независимые измерения и учитывая, что их число в данном случае 4, используем критерий Стьюдента и для 5%-ного уровня значимости получим -DHVCl3= - 142,3±9,7 ккал1моль.
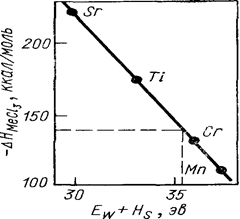
Рис. 10. Расчет энтальпии образования трихлорида ванадия по Л. П. Рузинову и др.: -DHVCl3 = 142 ккал/моль.
В справочной литературе энтальпию обычно приводят для стандартного состояния вещества при температуре 25°С. Значение энтальпии при другой температуре Т2 можно вычислить по уравнению Кирхгофа:
T2
DHT2 = DHT1 + ∫ DCp (9)
T1
где DHT2- известный тепловой эффект реакции при T1; DCp - разность в теплоемкости конечных и исходных продуктов реакции (зависящая определенным образом от температуры). Если в исследуемом интервале температуры наблюдается фазовый переход или полиморфное превращение, то DH возрастает на теплоту этого перехода или превращения.
ЭНТРОПИЯ
Изменение энтропии в результате химической реакции равно разности энтропии продуктов и исходных веществ. Энтропию веществ в газообразном состоянии можно рассчитать статистическим методом.
Существует значительное число эмпирических и полуэмпирических методов расчета. Ниже приведены примеры некоторых из них.
В. А. Киреев предложил рассчитывать энтропию по формуле:
S = åviSi + DS,
где vi - число однотипных атомов, входящих в соединение; Si - энтропия атомов, входящих в соединение; DS - изменение энтропии в реакции образования соединения из элементов. Это изменение определяется по аналогичным данным для родственных веществ. Например, для ди- и трихлоридов титана
DSTiCl2 = STiCl2 - STi - SCl2 = 23,8 - 7,2 - 53,3 = -36,7 кал/(моль. град);
DSTiCl3 = STiCl3 - STi - 1,5SCl2 = 30,6 — 7,2 — 1,5 . 53,3 = - 56,6 кал/(моль . град).
Принимаем, что для хлоридов циркония DSZrCl2 =DSTiCl2 и DSZrCl3 =DSTiCl3. Тогда
DSZrCl2 = SZrCl2 – SZr - SCl2 = 9,3 + 53,3 - 36,7 == = 25,9 кал/{моль . град),
DSZrCl3 = 9,3 + 1,5 . 53,3 - 56,6 = 32,7 кал/(моль . град).
Изменение энтропии образования соединения можно рассчитать по формуле:
DSi = DSfa + (åvkSki - åvk. Sk),
где Sfa - атомная энтропия образования соединения; Ski - энтропия атомов в состоянии идеального газа, по Дроссбаху.
Значение Ski - Sk для циркония равно -33,8 и для хлора -12,8 кал/(моль. град). Атомная энтропия образования для дихлоридов и трихлоридов циркония, найденная как среднее из соответствующих величин родственных соединений, равна соответственно -92,6 и -129,1 кал/ (моль . град). Тогда
DSfZrCl2 = -92,6 + 33,8 + 2 . 12,8 = -33,2 кал1(моль . град};
DSfZrCl3 = -129,1 + 33,8 + 3 . 12,8 = — 56,9 кал/(моль . град).
Отсюда
SZrCl2 = - 33,2 + 9,3 + 53,3 = 29,4 кал1(моль . град);
SZrCl3 = - 56,9 + 9,3 + 1,5 . 53,3 = 32,4 кал1(моль . град).
Дроссбах в случае хлоридов металлов предложил следующее уравнение для определения энтропии:
SMeCl2 = 24,2 lgM - 26,2,
SMeCl3 = 23,8 lgM- 22,4,
где М — молекулярная масса хлорида.
Для ди- и трихлорида циркония
SZrCl2 = 24,2 lg 162,5 - 26,2 = 26,9 кал/(моль . град);
SZrCl3 = 23,8 lg 197,7 - 22,4 = 32,1 кал/(моль . град).
Латимер предлагает рассчитывать энтропию как сумму значений энтропии атомов в соединении с учетом их валентности:
SZrCl3 = nSCl + SZr
Для хлора в зависимости от валентности катиона Латимер предлагает значение энтропии, равное 8,1 для соединений с двухвалентным катионом и 6,9 с трехвалентным катионом. Энтропия циркония в соединении равна 12,1 кал/(атом . град). Тогда
SZrCl2 = 2 . 8,1 + 12,1 = 28,3 кал1(моль . град);
SZrCl3 = 3 . 6,9 + 12,1 = 32,8 кал1(моль . град}.
Считая данные, полученные различными методами, за независимые и используя распределение Стьюдента для 5%-ного уровня значимости, получаем погрешность ±0,5: SZrCl3 = 32,6 ± 0,5 кал/(моль . град).
Энтропия сложных химических соединений в кристаллическом состоянии принимается равной сумме значений энтропии более простых составных частей этих соединений в кристаллическом состоянии в тех же условиях. Так, энтропию силикатов рассчитывают как сумму значений энтропии составляющих окислов. По Н. Н. Дрозину, если расположить соединения одного типа в порядке возрастания их молекулярной массы, энтропия данного соединения равна полусумме значений энтропии соседних соединений. По Веннеру, энтропия твердых соединений линейно зависит от логарифма молекулярной массы S==AlgM + B, где М - молекулярная масса; А и В - константы для подобных веществ.
А. Ф. Капустинский и К. Б. Яцимирский предложили метод расчета энтропии кристаллических соединений ионного типа, основанный на аддитивности энтропии ионов в кристалле. Последние вычисляют по уравнению:
S = 3/2 RlnA – 1,5z2/r,
где А - атомная масса; z - заряд иона; r - радиус иона, Å. Энтропию можно рассчитать сравнительными методами по М. X. Карапетьянцу. Если имеются данные об энтропии и теплоемкости для групп однотипных соединений, энтропию можно рассчитать по уравнению:
So298 = а + bСр,
где а и b — константы для данной группы однотипных соединений.
Энтропия однотипных соединений связана линейной зависимостью:
So298,I = а + b So298,II,
где а и b — константы.
Энтропию при температуре, отличной от приведенной в справочной литературе, рассчитывают графически или аналитически. В последнем случае
SoT = So298 + (Cp/T)dT (10)
Если в исследуемом интервале температуры происходит фазовый переход или полиморфное превращение, это должно быть учтено при вычислении абсолютной энтропии:
Ta®b Tпл
SoT = So298 + ∫(Cp/T)dT + DHa®b/Ta®b + ∫ (Cpb/T)dT + DHпл/Тпл +
298 Ta®b
Tисп T
+ ∫ (Cpж/T)dT + DHисп/Тисп + ∫ (Cpг/T)dT (11)
Tпл Tисп
ТЕПЛОЕМКОСТЬ
Знание теплоемкости необходимо для расчета термодинамических функций при температуре, отличной от той, при которой они были определены.
Теплоемкость газов с несложными молекулами можно достаточно точно рассчитать до очень высокой температуры статистическими методами из молекулярных параметров (момента инерции молекулы, собственных частот колебаний и т. д.).
Теплоемкость твердых тел при низкой температуре (до комнатной) можно рассчитать по уравнениям Планка-Эйнштейна, Дебая, Тарасова и т. д. При температуре выше комнатной теплоемкость как твердых тел, так и газов обычно рассчитывают из эмпирических уравнений, имеющих форму степенных рядов. В качестве примера для расчета теплоемкости элементов и сложных бескислородных соединений можно рассмотреть уравнение, предложенное Ландия и связывающее теплоемкость и энтропию:
СVат = 6,6 . (2200/Sат .Т)
где СVат - атомная теплоемкость при постоянном объеме; Sат = Sсоед/n (n- число атомов в соединении).
Уравнение имеет более сложный вид при температуре выше характеристической, а также для сложных кислородсодержащих соединений.
Теплоемкость при постоянном давлении связана с теплоемкостью при постоянном объеме формулой
Срат = СVат+ aТ3/2,
Где a = 1,24/Тпл . (СатV,298)2 Т3/2 .10-3.
Теплоемкость веществ можно также определить, используя сравнительные методы расчета.
ЭНЕРГИЯ ГИББСА
Изменение энергии Гиббса реакции в стандартных условиях DGo, но при температуре, отличной от приведенной в справочных данных, рассчитывают с учетом изменения теплоемкости системы:
T Т
DGoT = DНo298 - ТDSo298 + ∫DCpdT -Т ∫(-Cp/T)dT (11)
298 298
Отсюда легко получить формулы для приближенного расчета DGoT, принимая DCp = 0 в рамках первого приближения и DCp = const в рамках второго приближения. По первому приближению
DGoT = DНo298 - ТDSo298
Первое приближение дает удовлетворительные результаты для многих реакций до 500—600° К. Условие DCp = 0 предполагает отсутствие фазовых превращений, особенно связанных с появлением газообразной фазы.
В рамках второго приближения
DGoT = DНo298 - ТDSo298 – aTM0
где а = DCp = const.
Выражая зависимость DCp от температуры в виде степенного ряда:
DCp = DГ0 + DГ1Т + DГ2Т2 + …
где Г0, Г1, Г2,...- коэффициенты в уравнениях зависимости теплоемкости от температуры типа Cp = Г0 + Г1Т + Г2Т2 + …, М. И. Темкин и Л. А. Шварцман предложили удобный и быстрый метод расчета DGoT при различной температуре. Разность итегралов
T Т
∫DCpdT -Т ∫(-Cp/T)dT
298 298
в уравнении разбивается на сумму:
DГ0(lnT/298 + 298/T –1) + DГ1(T/2 + 298/2T –298) + DГ3(T/3 + 298/3T –2982/2) + …
Величины, стоящие в скобках, являются функциями только температуры. Их значения, обозначенные как М0 для первой скобки, M1 для второй скобки и M2 для третьей, даны в справочных таблицах для различных температур.
Расчет DGo высокотемпературного процесса часто связан с необходимостью учитывать энтальпию (DНф.п.) и энтропию DSф.п.= DНф.п./Тф.п. фазовых переходов и различие в теплоемкости системы до и после фазового перехода. Расчетная формула в этом случае имеет более сложный вид:
n n 2 2 n
DGoT = DHo298 + TDSo298 + ∑DНф.п. - ∑DНф.п./Tф.п. - T(∑DГiMi + ∑ ∑DDijDMij)
i=1 i=1 i=0 i=0 j=1
где Тф.п. - температура фазового перехода; DDij - изменение коэффициентов степенного ряда теплоемкости системы в температурном интервале между фазовыми переходами; DМij - изменение Mi на участке между Тф.п. и Т (DMij = Mij – Мij-1); n—число фазовых переходов.
Для большинства процессов зависимость DGoот температуры в интервале между фазовыми переходами в пределах погрешности можно выразить прямой. Графически эта зависимость может быть выражена в виде ломаной линии с изломами в точках фазовых переходов. Для ее построения достаточно рассчитать значение DGoф.п. соответствующее температуре фазовых переходов.
Проиллюстрируем это примером расчета DGo для реакции получения титана из тетрахлорида восстановлением магнием. Расчет выполнен Л. П. Ру-зиновым и др.
Реакция TiCl4 + 2Mg ® Ti + 2MgCl2 может сопровождаться следующими фазовыми переходами: переход TiCl4 из жидкого состояния в газообразное, переход Mg из твердого состояния в жидкое, переход MgCl2 из твердого состояния в жидкое, переход Mg из жидкого состояния в газообразное. Переход Ti из a-модификации в b не учитывался. Данные, необходимые для расчета сведены в табл. 7.
Таблица 7
Некоторые термодинамические характеристики веществ, участвующих в реакции TiCl4 + 2Mg ® Ti + 2MgCl2
| вещество | Агрегатное состояние | -DНo298, ккал/моль | So298, кал/моль | Тпл, К | DНoпл, кал/моль | Т, К | DНoкип, кал/моль | Ср, кал/(моль . град) |
| TiCl4 | ж. г. | -192,0 - | 59,6 - | - - | - - | - | 9,92 - | 35,7 25,45 + 0,24.10-3Т – 2,36.105Т-2 |
| Mg | тв. ж. | 153,4 | 21,4 | 10,3 | - | - | 18,9 + 1,42.10-3Т – 2,06.105Т-2 22,1 | |
| Ti | тв. | 0,0 | 7,3 | 5,28 + 2,4.10-3Т | ||||
| MgCl2 | тв. ж. г. | 0,0 - - | 7,77 - - | - - | 2,1 - - | - - | - 39,6 - | 5,33 + 2,45.10-3Т – 0,103.105Т-2 7,88 4,98 |
Пример расчета.
Температура 298° К:
DHo298 = -2 .153,4 + 192= -114,8 ккал = 114800 кал;
DSo298 =7,3 + 2 . 21,4 - 59,6 - 2 . 7,77= -25,04 кал;
DGo298 = - 114 800 + 298 . 25,04 = -107 230 кал.
DCp = 2Cтвр(MgCl2) + 2Cтвр(Ti) - 2Cтвр(Mg) - 2Cжр(TiCl4)= -3.28 + 0.34.10-3Т – 3,914.105Т2;
DGo410 = -114 800 + 410 . 25,04 - 410(-3,28 . 0,0465 + 0,34 . 0,0155 - 3 914 . 0,0427) = = -114 800 + 10 266 + 410 . 0,31 = -103824 кал.
Температура 923°К:
DCp = 2Cтвр(MgCl2) + 2Cтвр(Ti) - 2Cтвр(Mg) - 2Cгр(TiCl4)= 6,97 + 0,1.10-3Т - 6.274.10-5Т-2;
DM0 = M0(923) - M0(410) = 0,4532 - 0,0465=0,4067;
DM1 = M1(923) – M1(410) = 0,1961;
DM-2 = M-2(923) – M-2(410) = 0,2151;
DGo923 = -114 800 + 923 . 25,04 - 9920+ 9920. 923/410 + 923 .1,47 - 923(6,97 . 0,40674 + 0,1 . 0,1961 – 6,274 . 0,2151) = -114 800 + 23 112 – 9920 + 22 332 + 1357 –923 . 1,5048 =
= -69 388 кал.
Температура 987° К:
DCp = 2Cжр(MgCl2) + 2Cтвр(Ti) - 2Cжр(Mg) - 2Cгр(TiCl4)= 1,87 + 5,0.10-3Т – 1,76.10-5Т-2;
DM0 = M0(987) - M0(923) = 0,0468;
DM1 = M1(987) – M1(923) = 0,0339;
DM-2 = M-2(987) – M-2(923) = 0,0167;
DGo987 = -114 800 + 987 . 25,04 – 9920 - 4200 +9920 . 987/410 + 4200 . 987/510 + 987 . 1,77 - 987 . 2,5256 - 987(1,87 . 0,0468 + 5,0 . 0,0339 - 1,76 . 0,0167) = -114 800 + 24714 –9920 – 4200 + 23880 + 10 110 + 1750 – 2495 – 987 . 0.2276 = -72 932 кал.
Температура 1378°К:
DCp = 2Cжр(MgCl2) + 2Cтвр(Ti) - 2Cжр(Mg) - 2Cгр(TiCl4)= 8,27 + 2,16.10-3Т + 2,36.10-5Т-2;
DM0 = M0(1378) - M0(987) = 0,236;
DM1 = M1(1378) – M1(987) = 0,1855;
DM-2 = M-2(1378) – M-2(987) = 0,0705;
DGo1378 = -114 800 + 1378 . 25,04 – 9920 - 4200 + 20600 + 9920 . 1378/410 + 4200 . 1378/923 – 20 600 . 1378/987 + 1378 . 1,77 - 1378 . 2,5256 – 1378 .0,2276 - 1378(8,27 . 0,236 + 2,16 . 0,1855 + 2,36 . 0,0705) = -114 800 + 34 600 – 9920 - 4200 + 20 600 + 33 400 + 6300 - 28 800 + 2440 - 3485 - 314 - 1378 .251= - 67 687 кал.
-
Температура 1500° К:
DCp = 2Cжр(MgCl2) + 2Cтвр(Ti) - 2Cгр(Mg) - 2Cтвр(TiCl4)= 13,07 + 2,16.10-3Т + 2,36.10-5Т-2;
DM0 = M0(1500) - M0(1378) = 0,0691;
DM1 = M1(1500) – M1(1378) = 0,0604;
DM-2 = M-2(1500) – M-2(1378) = 0,0160;
DGo1500 = -114 800 + 1500 . 25,04 – 9920 - 4200 + 20600 – 67200 + 9920 . 1500/410 + 4200 . 1500/923 – 20 600 . 1500/987 + 67200.1500/1378 + 1500 . 1,7696 - 1500 . 2,5256 – 1500 .0,2276 – 1500.1,516 - 1500(13,07 . 0,0691 + 2,16 . 0,0604 + 2,36 . 0,016) = 64550 кал.
В табл. 8 и на рис. 11 представлены результаты расчета.
Таблица 8
DGoТ в точках фазовых переходов для реакции TiCl4 + 2Mg ® Ti + 2MgCl2
| Номер точки на рис. 11 | Фазовый переход | Т °К | - DGoТ |
| TiCl4(ж.) ® TiCl4(г.) Mg(тв.) ® Mg(ж.) MgCl2(тв.) ® MgCl2(ж.) Mg(ж.) ® Mg(г.) | 107,32 103,82 78,94 66,74 66,17 64,55 |
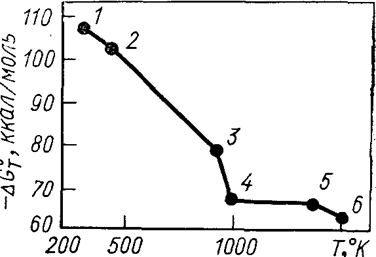
Рис.11. Изменение энергии Гиббса в точках фазового перехода для реакции: TiCl4 + 2Mg ® Ti + 2MgCl2
Зависимость DGo от температуры можно использовать для выбора наиболее благоприятной для процесса температуры. В данном случае максимально благоприятной с термодинамической точки зрения является наиболее низкая температура в рассмотренном интервале. Однако термодинамика однозначно не определяет оптимальную температуру процесса. В реальных условиях необходимо учитывать кинетику процесса, и она часто является определяющей.
Для расчета DGo могут быть привлечены сравнительные методы. Так, М. X. Карапетьянц на большом числе примеров показал хорошую линейную корреляцию изменения энергии Гиббса и энтальпии, отвечающую уравнению
DG = kDH + b.
Безэнтропийный расчет DGo298 является очень важным методом. Об этом можно судить хотя бы по тому, что теплота образования DНo298 известна примерно для 2,5 тысяч неорганических соединений и только меньше чем для одной трети из них известны одновременно и значения энергии Гиббса или Гельмгольца. Значения DGo298 ккал/моль более чем 600 веществ приведены в книге М. X. Карапетьянца «Методы сравнительного расчета физико-химических свойств». На огромном числе примеров показано, что точность этого метода расчета практически лимитируется точностью экспериментального определения DНo.
Аналогичным образом можно скоррелировать изменение энергии Гиббса для любой температуры с энтальпией при этой же температуре. Возможности определения DGo в этом случае зависят только от точности определения или расчета DНТ.
Дата добавления: 2019-04-03; просмотров: 526;
