Потенциальная кривая простейшего группового заземлителя

Потенциальная кривая простейшего группового заземлителя, состоящего из двух одинаковых полушаровых электродов, показана на рис. 2.9 жирной линией. Она получена сложением потенциальных кривых обоих электродов. Поскольку электроды одинаковы и находятся в одинаковых условиях, ток, стекающий в землю распределяется между ними поровну и, следовательно, их потенциальные кривые идентичны.

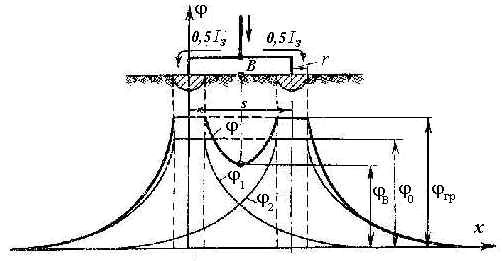
Рис. 2.9. Потенциальная кривая группового заземлителя, состоящего из двух одинаковых полушаровых электродов

Рассмотрим участок между электродами, т. е. кривые j ₁ и j ₂, которые в системе прямоугольных координат j , x с ординатой, проходящей через центр левой полусферы (рис. 2.9), выражаются следующими уравнениями, В:

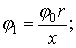
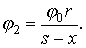
где j₀ - собственный потенциал полушарового заземлителя, определяемый но формуле (2.9), В; r - радиус полусферы, м; s - расстояние между центрами полусфер, м.

Искомое уравнение суммарной потенциальной кривой j , В, на участке между заземлителями определяется как:

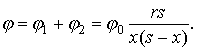(2.16)

Наибольший потенциал на поверхности земли будет при наименьшем значении x, т.е. при x=r. Это потенциал каждого из двух полушаровых электродов, входящих в состав рассматриваемого группового заземлителя, или потенциал группового заземлителя, В:

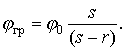(2.17)

Разделив (2.16) на (2.17), получим уравнение той же кривой, но выраженное через потенциал группового заземлителя, В:

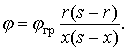(2.18)

Наименьший потенциал на поверхности земли между электродами будет в точке В, лежащей на средине отрезка s при x=s/2:

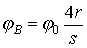или

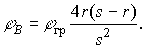
Из приведенных выражений видно, что с уменьшением s потенциал j _В возрастает, приближаясь к потенциалу группового заземлителя (наименьшее значение s=2r). Одновременно возрастает и j_гр, приближаясь к 2j₀ .

При большом значении s, например при s>=40м, j _В = 0, а j_гр= j_0.

Таким образом, с уменьшением расстояния между электродами группового заземлителя (начиная от 40 м) происходит выравнивание потенциала на поверхности земли. Подобный эффект наблюдается и при других групповых заземлителях, т.е. при иной форме электродов, большем числе их и любом взаимном размещении.