Решение систем линейных уравнений

Правило Крамера

Будем рассматривать систему n линейных уравнений с n неизвестными:

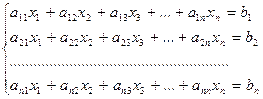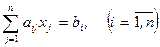или (4.1)

В матричной форме 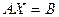, где квадратная матрица А имеет компоненты 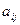, а матрицы-столбцы Х и В – соответственно 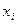и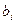

Теорема 4.1(Правило Крамера)Для того, чтобысистема линейных уравнений (4.1) имела единственное решение, необходимо и достаточно, чтобы 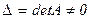. В этом случае решение данной системы будет иметь вид

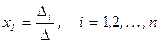, (4.2)

где 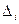– определитель матрицы, полученный из матрицы А заменой столбца c номером j на столбец свободных членов В

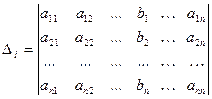
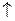
j-й столбец

Доказательство.

Докажем, что система (4.1) имеет решение 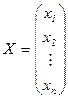, то есть выполняется равенство 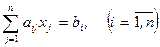. Умножив последовательно для всех 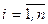обе части уравнений на алгебраические дополнения 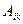и просуммировав результаты умножения по i, получим 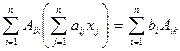, 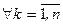.Перегруппируем слагаемые 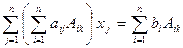. Так как сумма произведений элементов какого-либо столбца матрицы на соответствующие алгебраические дополнения (правило Лапласа) равна определитель данной матрица, а сумма произведений элементов столбца на алгебраические дополнения к элементам другого столбца равна нулю, то получаем 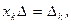Если 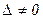, то решение существует и единственно:

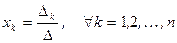
Пример 4.1.Решить систему уравнений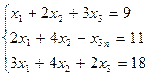

Вычисляем определители: ;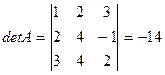

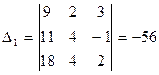
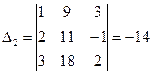
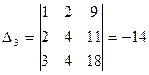
Значения неизвестных находим по формулам (1.6.2 ):

.

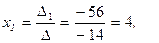
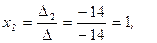
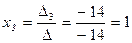Замечание 1. Если 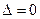и хотя бы один из определителей ∆_x, ∆_y, ∆_z отличен от нуля, то система (4.1) не имеет решений, т.е. она несовместна.

Замечание 2.Если 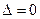и ∆_x = ∆_y = ∆_z = 0, то система (4.1) либо несовместной, либо неопределенной. В последнем случае, по крайней мере, одно из уравнений системы будет следствием других.