Double Cheb_1 (double x, int n)
{
double Tn, Tn_1 = x, Tn_2 = 1;
Switch (n)
{
case 0: return Tn_2;
case 1: return Tn_1;
default:
int i = 2;
while (i < = n)
{
Tn = 2 * x * Tn_1 - Tn_2;
Tn_2 = Tn_1;
Tn_1 = Tn;
++ i;
}
Return Tn;
}
}
При выполнении рекуррентных вычислений с вещественными значениями беспокоиться о переполнении значений вещественного диапазона приходится очень редко (особенно при использовании типа double). Но и здесь встречаются некоторые “подводные камни”.
Предостережение № 1. При определении условия продолжения цикла никогда не используйте проверку на точное равенство вещественных значений с помощью операции ==(впрочем, и в других условиях тоже). Например:
double a = 1.1, b = 0;
while ( ! (b == a) )
{
b = b + 0.1;
}
Такой цикл никогда не закончится, так как из-за погрешностей вычислений и представления вещественных значений точного равенства a и b при выбранных значениях никогда не будет (так, по крайней мере, происходит для этого примера в MS Visual C++ 2010). Лучше сделать так:
double a = 1.11, b = 0;
while ( b <= a )
{
b = b + 0.1;
}
Здесь цикл закончится гарантированно, и последнее значение b будет очень близко к 1.1.
Предостережение № 2.Остерегайтесь складывать (вычитать) очень большие и относительно малые вещественные значения. Например:
double a = 1e20, b = a, d = 1000;
int i = 1;
for ( int i = 1; i <= 1000000; ++ i)
{
b = b + d;
}
cout << b – a << endl;
Ожидается, что значение b после окончания цикла будет больше a на 1 000 000 000, однако разность между b и a оказывается равной 0. Это происходит, потому что величина d = 1 000 по отношению к значению a = 1e20 оказывается пренебрежимо малой из-за дискретности представления вещественных значений.
Если увеличить значение d и сделать его равным 10 000, то разность b – aокажется равной приблизительно 1.64e10, а не 1e10 как это следует из арифметики – достаточно грубая ошибка.
Для того, чтобы избавиться от этой неприятности, можно поступить так:
double a = 1e20, b = a, d = 1000, s = 0;
int i = 1;
for ( int i = 1; i <= 1000000; ++ i)
{
s = s + d;
}
b = b + s;
cout << b – a << endl;
Вот теперь мы увидим то, что ожидалось (или очень близкое к тому) и в первом и во втором случаях. Здесь мы сначала накопили отдельно сумму s относительно малых величин d, а затем уже относительно большое значение s добавили к b.
Инвариант цикла
Инвариантом называется логическое выражение, истинное перед началом выполнения цикла и после каждого прохода тела цикла, зависящее от переменных, изменяющихся в теле цикла.
Инварианты используются для доказательства правильности выполнения цикла, а также при проектировании и оптимизации циклических алгоритмов.
Порядок доказательства работоспособности цикла с помощью инварианта сводится к следующему:
- Доказывается, что выражение инварианта истинно перед началом цикла сразу после инициализации параметров цикла.
- Доказывается, что выражение инварианта сохраняет свою истинность до и после выполнения тела цикла; таким образом, по индукции, доказывается, что по завершении цикла инвариант будет выполняться.
- Доказывается, что при истинности инварианта после завершения цикла переменные примут именно те значения, которые требуется получить (это элементарно определяется из выражения инварианта и известных конечных значениях переменных, на которых основывается условие завершения цикла).
- Доказывается, что цикл завершится, то есть условие завершения рано или поздно будет выполнено.
- Истинность утверждений, доказанных на предыдущих этапах, однозначно свидетельствует о том, что цикл выполнится за конечное время и даст желаемый результат.
Инварианты используют не только для доказательства корректности циклов, но и при проектировании и оптимизации циклических алгоритмов.
Рассмотрим использование инварианта на примере реализации алгоритма Евклида для нахождения наибольшего общего делителя двух чисел.
Постановка задачи. Требуется найти наибольший общий делитель d двух целых чисел n и m: d = НОД(n, m).
Сформулируем инвариант цикла для нахождения НОД(n, m)следующим образом: пусть имеется пара чисел a и b таких, что НОД(a, b) = НОД(n, m). На каждом шаге цикла будем переходить к другой паре чисел a и b таких, что НОД(a, b) = НОД(n, m). И так будем продолжать до тех пор, пока значение НОД не станет очевидным. Таким образом, инвариант цикла сформулируем так: НОД(a, b) = НОД(n, m). Теперь стоит задача: как найти очередную пару чисел a и b, при которых значение инварианта не изменится.
Из математики (теория чисел) известно, что если d = НОД(n, m), то это же значениеd является и НОД(m, r), где r– остаток от деления nна m, то есть НОД(n, m) = НОД(m, r).
Например: НОД(126, 12) = НОД(12, 6) = НОД(6, 0) = 6
Алгоритм решения задачи можно представить так:
1. Начальная инициализация: пусть a = n, b = m. Очевидно, что НОД(a, b) = НОД(n, m).
2. Находим rи делаем a = b и b = r. При этом выражение НОД(a, b) = НОД(n, m)остается справедливым.
3. Как только b станет равно 0, тогда НОД(a, 0) = НОД(n, m) = a.
Программа, реализующая этот алгоритм:
int r, a = n, b = m;
// Инвариант: НОД(a, b) = НОД(n, m)
// Цикл заканчивается при b = 0, тогда НОД(a, 0) = a
While (b)
{
// Инвариант: НОД(a, b) = НОД(n, m) выполняется
r = a % b;
a = b;
b = r;
// Инвариант: НОД(a, b) = НОД(n, m) выполняется
}
// Инвариант: НОД(a, b) = НОД(n, m) выполняется
cout << “НОД (“ << n << “, ” << m << “) = ” << a << endl;
Можно предложить еще один алгоритм решения этой задачи, основанный на том же инварианте, но использующий другой способ нахождения следующей пары a и b: известно, что НОД(n, m) = НОД(n - m, m)приn > m и НОД(n, m) = НОД(n, m - n)приm > n. Например: НОД(126, 12) = НОД(114, 12) = НОД(102, 12) = … = НОД(18, 12) = НОД(6, 12) = НОД(6, 6) = 6. Но этот алгоритм является более затратным по сравнению с предыдущим.
Еще одним наглядным примером использования инварианта для проектирования цикла является реализация быстрого возведения чисел в целую положительную степень. Пример его реализации приведен в Приложении. Предлагается разобрать его самостоятельно.
В Приложении приведены программы, реализующие различные варианты итерационных вычислений, основанных на использовании рекуррентных соотношений и инвариантов.
Очень часто используются, так называемые, вложенные циклы. Примеры использования таких конструкций будут рассмотрены при изучении массивов.
Массивы
Массивы. Индексирование. Объявление массивов. Двумерные и многомерные массивы. Ввод-вывод массивов. Строки и тексты как массивы символов. Использование функций при работе с массивами. Управление памятью.
Понятие массива
Массив представляет собой индексированную последовательность однотипных элементов с заранее определенным количеством элементов. Все массивы можно разделить на две группы: одномерные и многомерные.
Аналогом одномерного массива из математики может служить последовательность некоторых элементов с одним индексом: 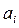 при i = 0, 1, 2, … n – одномерный вектор. Каждый элемент такой последовательности представляет собой некоторое значение определенного типа данных. Наглядно одномерный массив можно представить как набор пронумерованных ячеек, в каждой из которых содержится определенное значение:
при i = 0, 1, 2, … n – одномерный вектор. Каждый элемент такой последовательности представляет собой некоторое значение определенного типа данных. Наглядно одномерный массив можно представить как набор пронумерованных ячеек, в каждой из которых содержится определенное значение:
| 3.02 | 1.5 | 7.0 | -2.3 | 12.0 |
Это пример одномерного массива из 6 элементов, каждый из которых представляет собой некоторое вещественное значение и каждое из этих значений имеет индекс от 0 до 5.
А вот пример одномерного массива из десяти элементов, представляющих собой одиночные символы:
| ‘a’ | ‘b’ | ‘c’ | ‘+’ | ‘1’ | ‘2’ | ‘!’ | ‘#’ | ‘@’ | ‘&’ |
Каждый элемент в этих массивах определяется значением индекса элемента. Например, в последнем массиве элемент с индексом 5 равен символу ‘2’.
Двумерный массив – это последовательность некоторых элементов с двумя индексами: 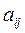 при i = 0, 1, 2, … nи j = 0, 1, 2, … m – двумерная матрица. Например, при n = 3 и m = 4:
при i = 0, 1, 2, … nи j = 0, 1, 2, … m – двумерная матрица. Например, при n = 3 и m = 4:
| j | |||||
| i | |||||
Эта матрица из 3-х строк и 4-х столбцов содержит 3 * 4 = 12 целых значений. Здесь уже каждый элемент определяется значениями двух индексов. Например, элемент с индексом i = 2 и индексом j = 1 равен целому значению 15.
Количество мерностей массивов может быть и больше двух, но при мерности большей 3 наглядно представить такой массив достаточно сложно.
Дата добавления: 2019-02-07; просмотров: 383;
