Unsigned Factorial (unsigned n)

{

unsigned i = 0; // Текущее значениеi

unsigned F = 1; // Текущее значениеi!

while (i < n)

{

++ i; // i = i + 1

F *= i; // F = F * i - текущее значениеi!

}

return F; // Возвращаем значение n!

}

Недостатком этой реализации является то, что с помощью этой функции можно вычислить n! только для n от 0 до 12. Значение 13! уже выходит за верхнюю границу диапазона значений типа unsigned и функция начинает возвращать неверные значения факториала. Для предотвращения получения неверных значений факториалов модифицируем функцию следующим образом:

Unsigned Factorial (unsigned n)

{

unsigned i = 0; // Текущее значениеi

unsigned F = 1; // Текущее значениеi!

while (i < n)

{

++ i; // i = i + 1

if (0xffffffffu / i < F ) // 0xffffffffu– максимальное значение типа unsigned

{

F = 0;

Break;

}

F *= i; // F = F * i - текущее значениеi!

}

return F; // Возвращаем значение n!

}

Добавленная проверка обнаруживает ситуацию, когда умножение предыдущего значения факториала на следующее значение i приведет к выходу полученного значения произведения за верхнюю границу диапазона значений типа unsigned. В этом случае значению факториала присваивается значение 0(факториал любого числа всегда больше 0), и с помощью инструкции break выполнение цикла прерывается. В этом случае функция вернет значение 0.

При такой реализации функцию Factorialв программе можно использовать, например, так:

Unsigned F, n;

…..

if (F = Factorial (n))

….. // Используем вычисленное значение факториала F

Else

cout << “Ошибка. Факториал числа ” << n << “ не может быть вычислен! \n”;

Важно. При рекуррентном накоплении сумм, произведений (степеней, факториалов) целых типов следует очень внимательно контролировать возможность выхода за границы диапазона значений используемого целого типа данных. При возникновении таких ситуаций поведение программы будет непредсказуемым.

Еще один пример. Требуется подсчитать сумму первых n элементов следующего степенного ряда:

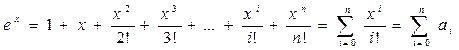
Если подойти к решению этой задачи “в лоб”, то получится следующая весьма неэффективная программа:

int n = 20; //Количество суммируемых элементов ряда

double x = 2.5; //Значение аргумента x

double S = 0; //Начальное значение суммы ряда

int i = 0; // Начальное значение индекса элемента ряда

while (i < n)

{

S = S + pow(x, i) / Factorial (i);

++ i;

}

cout << “Сумма первых ” << i << “ элементов ряда равна ” << S << endl;

Неэффективность этого варианта реализации объясняется двумя причинами. Во-первых, поскольку функция вычисления факториала представляет собой цикл, общее количество операций будет быстро расти с увеличением n. Во-вторых, нам вообще не удастся подсчитать сумму более чем 13 элементов этого ряда, так как при i = 13, функция вычисления факториала возвратит значение 0, и наша программа аварийно завершится с ошибкой “Деление на 0”. Избежать аварийного завершения программы можно, как это было описано выше – путем проверки значения факториала на 0 и прерывания цикла, однако более 13 элементов ряда все равно просуммировать не удастся.

Решить эту проблему поможет еще одно рекуррентное соотношение, связывающее очередное значение элемента ряда с его предыдущим значением.

Несложно заметить, что 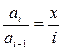откуда следует, что 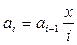при .

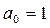Тогда можно предложить следующий вариант реализации:

int n = 20; //Количество суммируемых элементов ряда

double x = 2.5; //Значение аргумента x

double a = 1; // Значение первого элемента ряда

double S = 1; //Начальное значение суммы ряда при i = 0

int i = 1; // Начальное значение индекса элемента ряда

while (i < n)

{

a = a * x / i ;

S = S + a;

++ i;

}

cout << “Сумма первых ” << i << “ элементов ряда равна ” << S << endl;

В этой реализации недостатки предыдущего варианта программы отсутствуют. Удалось избавиться и от вычисления факториала, и от возведения в степень аргумента x. Теперь количество операций на каждой итерации постоянно и равно 4. Программа позволяет находить сумму практически любого количества элементов ряда.

Более сложный вариант рекуррентного соотношения. Требуется написать функцию для получения значения многочлена Чебышева первого рода степени n >= 0 , задающегося следующим рекуррентным соотношением:

Реализация: