Сокращенные и тупиковые нормальные формы.
Задача нахождения сокращенных и тупиковых нормальных форм БФ возникает при решении задачи минимизации, как ее частный случай: представить БФ в нормальной форме с использованием наименьшего возможного количества букв и функций.
Эта задача минимизации, называемая канонической, является основной при синтезе комбинационных схем.
В общем случае под минимизацией БФ понимают нахождение этой функции в виде суперпозиции функций, составляющих какой-либо базис или систему БФ.
Сокращенные формы (ДСНФ и КСНФ) получают из совершенных (СДНФ, СКДФ) путем склеивания элементарных конъюнкций (дизъюнкций) одного ранга по принципу ”каждая с каждой”.
Например, 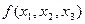 , представленную таблицей истинности табл. 1, необходимо привести к форме КСНФ. Поместим в первый столбец все ее конституенты «0» (табл. 2) и склеим все возможные варианты по принципу «каждая с каждой» одновременно помечая «
, представленную таблицей истинности табл. 1, необходимо привести к форме КСНФ. Поместим в первый столбец все ее конституенты «0» (табл. 2) и склеим все возможные варианты по принципу «каждая с каждой» одновременно помечая « 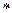 » участвующих в склейке и записывая результаты во второй столбец.
» участвующих в склейке и записывая результаты во второй столбец.
Затем повторим эту операцию с элементарными дизъюнкциями второго столбца, получая третий и т.д., до тех пор, пока в текущем столбце будут встречаться склеиваемые дизъюнкции.
Заметим, что в скобках приведены номера дизъюнкций предыдущего столбца, участвующие в получении данной дизъюнкции.
Табл. 1 Табл. 2
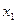
| 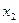
| 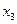
| 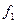
| Конституенты "0" | Эл. дизъюнкц. ранга 2 | Эл. дизъюнкц. ранга 1 | |||
1) 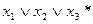 2)
2) 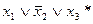 3)
3) 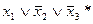 4)
4) 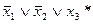 5)
5) 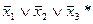
|  1) 1) 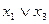 (1,2)*
2) (1,2)*
2) 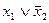 (2,3)*
3) (2,3)*
3) 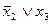 (2,4)*
4) (2,4)*
4) 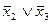 (3,5)*
5) (3,5)*
5) 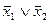 (4,5)* (4,5)*
| 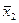 (2,5) (2,5)
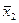 (3,4) (3,4)
| |||||||
В функцию 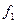 в форме КСНФ попадут все непомеченные дизъюнкции всех столбцов табл. 2
в форме КСНФ попадут все непомеченные дизъюнкции всех столбцов табл. 2
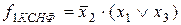 .
.
Покажем получение ДСНФ на примере функции 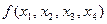 , заданной в табл. 3.
, заданной в табл. 3. 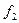 состоит из 8 конституент. "1", по которым и произведем склеивание, аналогично предыдущему примеру для КСНФ. В табл. 4 показано склеивание конституент «1» и элементарных конъюнкций функции записанных в виде комбинаций 1 и 0.
состоит из 8 конституент. "1", по которым и произведем склеивание, аналогично предыдущему примеру для КСНФ. В табл. 4 показано склеивание конституент «1» и элементарных конъюнкций функции записанных в виде комбинаций 1 и 0.
Табл. 3 Табл. 4
| x1 x2 x3 x4 | f2 | Конституенты 1 | Конъюнкции ранга 3 | Конъюнкции ранга 2 | |
| 0 0 0 0 | 1) 0 0 0 0 * | 0 0 0 _ (1, 2) * | 0 _ 0 _ (1, 4) | ||
| 0 0 0 1 | 2) 0 0 0 1 * | 0 _ 0 0 (1, 3) * | 0 _ 0 _ (2, 3) | ||
| 0 0 1 0 | 3) 0 1 0 0 * | 0 _ 0 1 (2, 4) * | |||
| 0 0 1 1 | 4) 0 1 0 1 * | 0 1 0 _ (3, 4) * | |||
| 0 1 0 0 | 5) 0 1 1 1 * | 0 1 _ 1 (4, 5) * | |||
| 0 1 0 1 | 6) 1 0 1 0 * | _ 1 1 1 (5, 8) * | |||
| 0 1 1 0 | 7) 1 1 1 0 * | 1 _ 1 0 (6, 7) * | |||
| 0 1 1 1 | 8) 1 1 1 1 * | 1 1 1 _ (7, 8) * | |||
| 1 0 0 0 | |||||
| 1 0 0 1 | |||||
| 1 0 1 0 | |||||
| 1 0 1 1 | |||||
| 1 1 0 0 | |||||
| 1 1 0 1 | |||||
| 1 1 1 0 | |||||
| 1 1 1 1 |
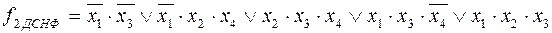
Форма ДСНФ для функции f2 является избыточной, однако сократить ее по основным законам булевой алгебры не представляется возможным. Определим, какие конъюнкции в форме ДСНФ можно исключить без изменения таблицы истинности функции.
Итак, все конституенты «1» функции являются обязательными. Конъюнкции более низкого ранга получены из конституент «1» путем склеивания и значит, содержат в себе значения исходных конституент.
Определение минимального количества дизъюнкций с пониженным рангом, содержащих в себе все конституенты единицы, производится с помощью импликантной таблицы (табл. 5).
Табл. 5
 Иден-тиф. строки Иден-тиф. строки
| Конституенты Простые единицы Импликанты | ||||||||
| a | 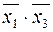
| X | X | X | X | ||||
| b | 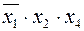
| X | X | ||||||
| c | 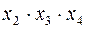
| X | X | ||||||
| d | 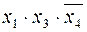
| X | X | ||||||
| e | 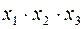
| X | X | ||||||
Нам необходимо определить по ней варианты покрытий всех столбцов (конституент "1") строками (простыми импликантами).
Итак, в покрытие П должны входить все конституенты единицы функции:
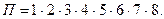
При этом каждая из конституент может быть представлена в покрытии одной или несколькими простыми импликантами, например,
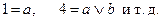
То есть, 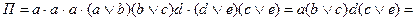
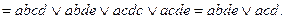
Функция 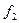 , таким образом, имеет 2 тупиковые формы:
, таким образом, имеет 2 тупиковые формы:
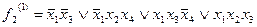
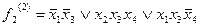
Тупиковой формой функции 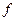 называют такую систему простых импликант, соответствующих
называют такую систему простых импликант, соответствующих 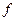 , при удалении из которой хотя бы одной импликанты система перестает соответствовать
, при удалении из которой хотя бы одной импликанты система перестает соответствовать 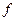 .
.
Среди тупиковых форм различают минимальные и кратчайшие.
Минимальная форма ДНФ или КНФ – это такая тупиковая ДНФ или КНФ, которая содержит минимальное количество переменных.
Кратчайшая ДНФ или КНФ – это тупиковая форма, содержащие минимальное количество элементарных конъюнкций или дизъюнкций.
В рассмотренном случае 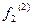 является одновременно МДНФ и КДНФ.
является одновременно МДНФ и КДНФ.
Для функций от небольшого количества переменных (до 5) кратчайшая и минимальная формы совпадают. Вероятность несовпадения увеличивается с ростом числа переменных функции.
3. МЕТОДЫ МИНИМИЗАЦИИ БУЛЕВЫХ ФУНКЦИЙ.
Методов минимизации существует достаточно много, но суть их сводится к построению различных алгоритмов, применяющих закон склеивания.
Рассмотрим два из подобных методов:
1) Метод Квайна – Мак-Класки;
2) Метод минимизации по картам Карно – Вейча.
Дата добавления: 2019-02-07; просмотров: 997;
