Величине D присвоить значение, равное значению X.

Не зная, что представляет собой эта задача, мы получим D=17 – правильный ответ, если строго выполним все пункты последовательно друг за другом. А между тем, это алгоритм решения задачи по определению наибольшего общего делителя двух натуральных чисел X и Y – знаменитый алгоритм Евклида.

Поскольку алгоритм как система простейших законченных операций, носит формальный характер, то на его основе всегда можно разработать программу действий для программно-управляемого электронного автомата, в частности компьютера, и осуществить машинное решение задачи. Таким образом, решение задач на основе алгоритмов может быть автоматизировано.

В связи с этим особое значение приобрели работы по описанию процессов управления автоматизированными объектами в виде алгоритмов. Получаемые при описании алгоритмы не всегда пригодны для непосредственного использования. Поэтому большое значение имеет проблема равносильных преобразований алгоритмов с целью их “улучшения”. Важным кругом проблем является оценка качества полученного алгоритма, то есть эквивалентность алгоритма исходному процессу, его экономичность (алгоритм должен позволять программе разместиться в памяти), эффективность, например, по быстродействию (никому не нужен прогноз погоды на позавчера) и нахождение в том или ином смысле оптимальных алгоритмов.

Свойства алгоритмов.Алгоритм должен быть составлен таким образом, чтобы исполнитель, в расчете на которого он создан, мог однозначно и точно следовать командам алгоритма и эффективно получать нужный результат.Алгоритмам присущ ряд свойств, которые и объясняют, почему исполнитель может получить решение какой-то задачи без особого труда. Если какое-то свойство не выполняется, то такое описание последовательности действий над заданными объектами будет называться не алгоритмом, апредписанием.

1. Дискретность. Одно из первых требований, которое предъявляется к алгоритму, состоит в том, что описываемый им процесс должен состоять из последовательности законченных действий–шагов. Возникающая в результате такого разбиения запись представляет собой упорядоченную совокупность четко разделенных друг от друга предписаний (команд, операторов, директив), образующих дискретную структуру алгоритма. Переход к следующему шагу возможен лишь после завершения предыдущего. Причем на каждом шаге выполняется простейшая операция, соответствующая одному из определенных простейших актов, на которые расчленяется определяемый алгоритмом процесс. Свойство алгоритма состоять из отдельных шагов и называется дискретностью.

2. Массовость. Это возможность применять алгоритм к различным вариантам исходных данных (например, алгоритм Евклида), то есть возможность решать любую задачу некоторого класса, описываемого данным алгоритмом. Свойство массовости значительно увеличивает практическую ценность алгоритма.

3. Понятность. Используемые на практике алгоритмы составляются с ориентацией на определенного исполнителя. Чтобы составить для него алгоритм, нужно знать, какие команды этот исполнитель может понять и выполнить, а какие – нет. У каждого исполнителя имеется своя система команд, даже у отдельно взятых компьютеров системы команд отличаются (например, компьютер с процессором Pentium без блока команд MMX не может выполнять приложения мультимедиа). Очевидно, составляя алгоритм для определенного исполнителя, например для станка с программным управлением, можно использовать только те команды, которые имеются в системе команд этого исполнителя. Это свойство алгоритмов и будем называть понятностью.

4. Результативность. Под результативностью алгоритма будем понимать существование таких вариантов исходных данных, для которых после конечного числа элементарных операций выполнение алгоритма заканчивается и дает искомый результат, и отсутствие таких вариантов, для которых процесс выполнения алгоритма приводит к неправильному результату. При этом допускается существование вариантов исходных данных, для которых не получается никакого результата либо потому, что процесс выполнения алгоритма безрезультатно обрывается в силу того, что к полученному промежуточному результату дальнейшее применение алгоритма не имеет смысла, либо потому, что этот процесс никогда не заканчивается (зацикливается).

В практике автора был случай, когда после решения задачи в течение четырех лет на очередной порции исходных данных задача зависла. После неоднократной проверки задачи на исходных данных за предыдущие отчетные периоды удалось обнаружить ошибку в алгоритме, которая проявилась только на определенном наборе исходных данных.

Широко известен также факт, нашумевший в конце 1994 года по поводу выпуска фирмой Intel первых процессоров Pentium. В более чем 5 млн. проданных процессоров была обнаружена ошибка алгоритма выполнения операции деления с плавающей запятой при определенных сочетаниях двух чисел, что незамедлительно сказалось на престиже и финансовом положении фирмы.

При многочисленных тестовых проверках процессора в течение нескольких месяцев летом 1994 г. специалисты фирмы пришли к выводу, что с ошибкой выполняется в среднем одна из 9 млрд. операций деления чисел с плавающей запятой. При самой интенсивной загрузке компьютера вычислительными операциями такая ошибка должна была происходить один раз в 27 лет. Поскольку это время значительно превосходило все мыслимые сроки эксплуатации процессора, то на фирме решили не придавать значения этому факту. Но тут-то и случилась беда. Доктор Томас Нейсли из колледжа небольшого городка Линчбург в штате Вирджиния занимался теорией чисел и много проводил вычислений с точностью до 19 знака после запятой. 13.06.94 г. он обнаружил несоответствие между имеющимися таблицами и результатами вычислений. Он долго перепроверял свои программы и, наконец, 19.10.94 г. обратился в фирму Intel, но в течение недели ответа не получил. 30.10. 94 г. по электронной почте он разослал серию посланий своим коллегам и всем, у кого есть компьютеры с такими процессорами, с просьбой проверить его результаты. Сеть буквально захлебнулась от посланий на эту тему. За считанные дни новость распространилась по всему миру. Множество людей бросились перепроверять свои расчеты и обнаружили, что беда не обошла и их. Телефонные линии в стране буквально раскалились, акции фирмы стремительно начали падать в цене, а новость появилась на первой полосе газет и в заголовках телевизионных новостей.

Фирма же вместо того, чтобы покаяться и извиниться, сделала вид, что будто бы ничего и не произошло заявив, что об ошибке мы знаем, но вероятность появления ее настолько мала, что процессоры менять не надо. Это только подлило масла в огонь. Людей раздражало главное – что фирма знала об ошибке раньше, чем ее обнаружили, и молчала. Фирме пришлось все-таки принести свои извинения и объявить, что она готова заменить процессоры на новые с условием доставки старых. Все сделали определенные выводы:

· фирма Intel поняла, что врать покупателям нельзя;

· показала свои возможности сеть Интернет;

· были обнаружены ошибки в действующих программах, в частности, в Excel 5.0 – при выполнении одной из функций.

Вот несколько пар чисел, при делении которых появлялась ошибка: 5505001:294911 правильный ответ – 18,66665197 , а компьютер давал результат – 18,66600093; 4195835:3145727 правильный ответ – 1,33382044, результат компьютера – 1,333739068; 962306957033:11010046 правильный ответ – 87402,6282027341, результат компьютера – 87399,5805831329.

5. Определенность. Каждый алгоритм строится в расчете на некоего исполнителя. Чтобы исполнитель мог решать задачу по заданному алгоритму, необходимо, чтобы каждая команда алгоритма всегда однозначно понималась и точно исполнялась. Запись алгоритма должна быть настолько четкой, полной и продуманной в деталях, чтобы у исполнителя не могло возникнуть потребности в принятии решений, не предусмотренных алгоритмом. Это значит, что любая команда, выполняемая много раз различными исполнителями, имеющими эту команду в своей системе команд, при одних и тех же исходных условиях всегда должна давать один и тот же результат. Алгоритм не должен оставлять места для произвола исполнителя. После выполнения каждой команды исполнитель должен знать, какую команду нужно выполнять следующей. Чтобы исключить возможность неоднозначного понимания команд алгоритма, для описания алгоритмов разработаны специальные формализованные алгоритмические языки, в которых каждое предложение имеет абсолютно точный смысл.

Способы записи и разработка алгоритмов. Для записи алгоритмов существуют различные способы. Одни из них ориентированы на исполнителя–человека, другие – на программно-управляемые электронные устройства, третьи являются вспомогательными для облегчения рассуждений. Алгоритм можно представить с помощью словесного или графического описания, в виде последовательности формул или в табличном виде.

Словесный способ. Словесный способ представляет собой текстовую запись последовательного выполнения определенных действий, приводящих к конечному результату. Форма записи команд произвольная, главное, чтобы она не допускала неоднозначных толкований и была понятной. Покажем это на примере нахождения наименьшей из двух величин.

1. Задать числовые значения величин A и B.

2. Если A<B, то положить Y равным A, иначе положить Y равным B.

3. Записать в ответе значение Y.

4. Конец

Словесный способ чаще всего используется на начальных этапах изучения поставленной задачи. При этом задача разбивается на отдельные самостоятельные крупные блоки, имеющие функциональную законченность. Затем эти блоки детализируются и разбиваются на более мелкие, которые потом объединяются в один алгоритм. Этот способ в основном рассчитан на исполнение алгоритма человеком.

Графический способ.При этой форме записи алгоритмов отдельные команды изображаются в виде плоских геометрических фигур, внутри которых описываются словесно или с помощью формул выполняемые действия. Используемые графические фигуры блоков стандартизированы. Существует ГОСТ 19.003-80. Схемы алгоритмов и программ. Обозначения условные графические.

Прямоугольник часто называют элементом общей обра-ботки. Ромб часто называют элементом принятия решений и исполь- зуют для организации ветвления или цикла в алгоритме. Последовательность выполнения блоков, то есть переход от одного блока к другому, обозначается стрелками. Этот способ имеет ряд преимуществ благодаря наглядности. Он имеет четкую и ясную структуру, легко поддается проверке. Такие алгоритмы называют блок-схемами.

Блок- схема – это ориентированный граф, вершины которого могут быть одного из типов, представленных на рис. 7.

Из этих четырех элементарных блок-схем может быть получена любая структурная блок-схема. Важной особенностью приведенных структур является то, что они имеют один вход и один выход. Бывает, что в процессе поиска алгоритм не может быть представлен в структурном виде. Тогда приходится применять специальные приемы, преобразования неструктурного алгоритма в структурный. Это и дублирование блоков, введение вспомогательных постоянных (метод Ашкородта-Манна), введение логических переменных - признаков (метод логического признака), объединение условий продолжения цикла и т.д.

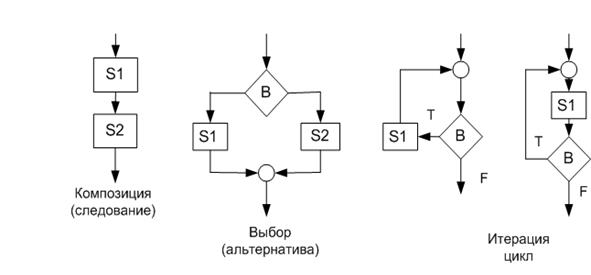
Рис.7

В более широком плане структурное программирование допускает большее разнообразие элементарных структур управления, чем предложенные четыре. На рисунке справа представлены еще две элементарные структуры: выполнение одной альтернативы и оператор множественного выбора. Причиной для расширения множества структур является требование удобства и естественности.

В качестве примера составим алгоритм вычисления величины Z, исходя из условий:

Z =

Структурная блок-схема алгоритма, составленная из приведенных выше простейших структур, представлена на рис. 8.

.Алгоритмический язык.В ал-горитмическом языке используется ограниченное число слов, смысл и способы употребления которых строго определены. Эти слова на-зываются служебными. Исходные данные задачи называются аргу-ментами и перечисляются после записанного сокращенно служеб-ного слова арг. Для выявления структуры алгоритмов обычно при их записи каждую команду пишут в отдельной строке, делают отсту-пы от начала строки, выделяя от-дельные блоки или процедуры ал-горитма, чтобы была наглядность и легкость его понимания.

Для простоты понимания запи

шем на русском языке алгоритм нахождения наименьшего числа из двух. Здесь курсивом выделены

служебные слова. Рис. 8

При разработке алгоритмического языка стремятся к тому, чтобы он удовлетворял следующим требованиям:

· легкость изучения, понимания и применения;

· компактность описания процессов;

· удобство использования в публикациях;

· универсальность.

Некоторые из этих требований противоречат одно другому, например, второе и четвертое, так как нельзя сделать компактным универсальное. Однако при создании языков находят компромиссы, удовлетворяющие всем требованиям.

Язык программирования высокого уровняслужит для записи алгоритмов в таком виде, в котором они могут быть исполнены компьютером, то есть по существу в виде компьютерных программ. Компьютерная программа - это алгоритм, доведенный до машинного исполнения. Запишем алгоритм нашего примера на языке программирования высокого уровня Бейсик:

INPUT A,B

20 IF A<B THEN Y=A ELSE Y=B

PRINT Y

ЕND

Разработка алгоритмов решения задач на ЭВМ требует специальных навыков и знания определенных приемов их записи. Существует весьма большое количество всевозможных приемов и методов разработки алгоритмов. Основным приемом является структурный подход, то есть разбивка всего алгоритма на отдельные структуры, которые затем объединяются в единый алгоритм. Особо следует обращать внимание на организацию циклов. Практически не бывает алгоритмов, в которых не использовались бы циклические структуры. Они являются основными частями всяких практически используемых алгоритмов. Количество повторений цикла может быть известно заранее – арифметические циклы, или заранее неизвестно – итерационные циклы. Для тех и других циклов существует множество способов их организации. Нередко взаимосвязь между циклами в алгоритме бывает довольно сложной: циклы переплетаются друг с другом или входят один в состав другого. Организация цикла – наиболее сложная задача, так как от оптимального построения циклов зависит время выполнения алгоритма или быстрота решения задачи.

В практике автора был случай, когда для решения задачи оптимального планирования была приобретена программа для ЭВМ ЕС, которая при матрице примерно 1000х900 выполнялась более 22 часов непрерывно. Дело оказалось в том, что обращение к дискам (медленным устройствам) было организовано в сложном цикле.

Приведем несколько методов построения алгоритма.

Метод частных целей лежит в основе решения многих задач и составляет основу алгоритмизации. Суть его сводится к вопросу: " Можно ли данную задачу разбить на последовательность более простых?" Конечно, в конкретной сложной задаче очень часто трудно указать способ ее разбиения на набор более простых задач. Здесь большое значение имеют опыт и искусство специалиста.

Метод подъема. Этот метод, как и предыдущий, можно отнести к одному из общих "рецептов" разработки алгоритмов. Алгоритм начинается с принятия начального предположения или построения начального решения задачи. Затем идет уточнение решения, алгоритм дорабатывается более подробно и так продолжается движение "вверх" от начального уровня по направлению к получению наилучшего решения.

Программирование с отходом назад. Этот метод применяется для разработки программ искусственного интеллекта, независимо от того к чему он прилагается – программирование игр, распознавание образов, выбор решений и т.д. Здесь основным является перебор вариантов. Это сложная задача, так как алгоритмы перебора ищут решение не по заданным правилам вычислений, а путем проб и ошибок. Схема их не укладывается в схемы ветвлений и циклов. Ситуация часто осложняется тем, что прямыми методами перебор всех возможных вариантов осуществить нельзя из-за их огромного количества. Метод алгоритмизации с отходом назад позволяет осуществить организованный исчерпывающий поиск требуемого решения задачи. При этом часто удается избежать перебора всех возможных вариантов.

Наиболее сложным разделом алгоритма перебора вариантов является движение назад (откат) и связанная с этим необходимость восстановления номера последнего варианта предыдущего хода. Этот вопрос автоматически решается при рекурсивной организации алгоритма.

Имеется еще ряд методов и способов разработки алгоритмов, используемых программистами высокой квалификации, но из-за их сложности эти методы здесь не рассматриваются.

Лекция 12