Лекция 3. Модели факторного, дисперсионного и регрессионного анализа.
Основные понятия дисперсионного анализа.
Первоначально дисперсионный анализ был предложен Рональдом Фишером (1890 – 1962) в 1925 году для обработки результатов агрономических опытов по выявлению условий, при которых испытываемый сорт сельскохозяйственной культуры даёт максимальный урожай.
Современные приложения дисперсионного анализа охватывают широкий круг задач техники, экономики, социологии и биологии.
В настоящее время дисперсионный анализ определяется как статистический метод, предназначенный для выявления влияния отдельных факторов на результат эксперимента.
Дисперсионный анализ часто используется для выявления влияния на изучаемый показатель некоторых факторов, обычно не поддающихся количественному измерению.
Модели дисперсионного анализа в зависимости от числа факторов, влияние которых изучается, подразделяются на однофакторные, двухфакторные и т.д.
По цели исследования выделяют детерминированные, случайные и смешанные модели.
В детерминированной модели уровни всех факторов заранее фиксированы и проверяют именно их влияние.
В случайной модели уровни каждого фактора получены как случайная выборка из генеральной совокупности уровней фактора.
В смешанной модели уровни одних факторов заранее фиксированы, а уровни других – случайная выборка.
Изучаемую случайную величину Х (на которую влияют один или несколько факторов) в дисперсионном анализе называют результативным признаком.
Суть метода дисперсионного анализа состоит в разложении общей вариации изучаемого показателя на части, соответствующие раздельному и совместному влиянию факторов, и статистическом изучении этих частей с целью выяснения приемлемости гипотез о существовании влияний факторов.
Рассмотрим сначала подробно однофакторную модель дисперсионного анализа.
Пусть имеется результативный признак Х и фактор А, с уровнями А1, А2, ..., Аr. При i – ом уровне фактора А (где i меняется от 1 до r) случайная величина Х приняла значения 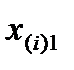 ,
, 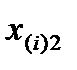 ,...,
,..., 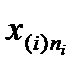 .
.
В основе дисперсионного анализа лежит следующая вероятностная модель:
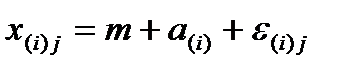 ,
,
где 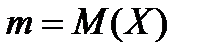 - математическое ожидание случайной величины Х;
- математическое ожидание случайной величины Х;
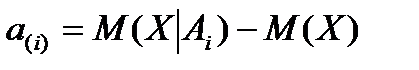 - эффект влияния уровня Аi на результативный признак;
- эффект влияния уровня Аi на результативный признак;
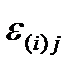 - случайный остаток, отражающий влияние всех остальных (неучтённых) факторов.
- случайный остаток, отражающий влияние всех остальных (неучтённых) факторов.
Основными предположениями дисперсионного анализа являются два следующих.
1) Остатки 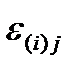 взаимно независимы для любых i и j.
взаимно независимы для любых i и j.
2) Распределение остатков 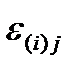 является нормальным и не зависит от i и j,
является нормальным и не зависит от i и j,
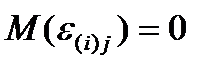 ,
, 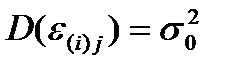 .
.
Величины 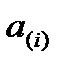 могут быть как постоянными (для детерминированной модели), так и случайными (для случайной модели). В последнем варианте
могут быть как постоянными (для детерминированной модели), так и случайными (для случайной модели). В последнем варианте 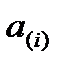 полагают независимыми друг от друга и от случайных остатков.
полагают независимыми друг от друга и от случайных остатков.
В любой модели зависимость 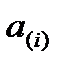 от уровня фактора i указывает на влияние фактора на результативный признак, и следовательно, если
от уровня фактора i указывает на влияние фактора на результативный признак, и следовательно, если 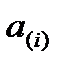 не зависят от уровня фактора i , то это говорит о том, что фактор А не влияет на результирующий признак Х.
не зависят от уровня фактора i , то это говорит о том, что фактор А не влияет на результирующий признак Х.
Целью исследования является выяснение изменчивости величин 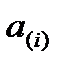 в зависимости от уровня фактора, в частности, гипотеза об их равенстве. Если
в зависимости от уровня фактора, в частности, гипотеза об их равенстве. Если 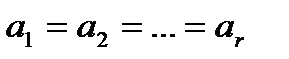 , то можно сделать вывод о том, что фактор А не влияет на результирующий признак Х.
, то можно сделать вывод о том, что фактор А не влияет на результирующий признак Х.
Основная идея дисперсионного анализа основана на разложении суммы квадратов отклонений.
Исходными данными в дисперсионном анализе являются r групп наблюдений над случайной величиной Х (группа характеризуется определенным значением фактора):
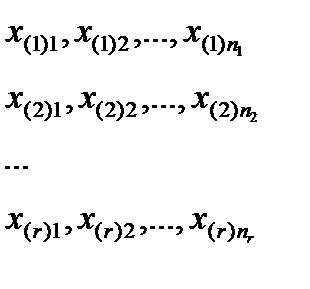
Общее количество наблюдений (объем выборки):
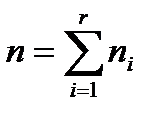 .
.
Оценкой математического ожидания (согласно методу моментов) генеральной случайной величины Х является среднее арифметическое всех выборочных значений:
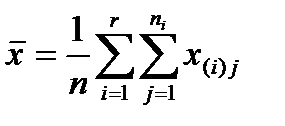 .
.
Оценкой дисперсии (по методу моментов) генеральной случайной величины Х является нормированная сумма квадратов:
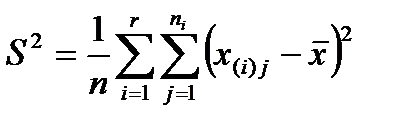 .
.
Основная идея дисперсионного анализа заключается в разбиении последней суммы квадратов отклонений на несколько компонент, каждая из которых соответствует предполагаемой причине изменения значений 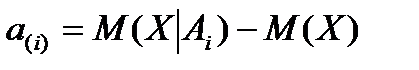 .
.
Оценка условного математического ожидания 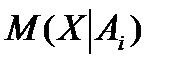 - это среднее арифметическое выборочных данных в i-ой группе:
- это среднее арифметическое выборочных данных в i-ой группе: 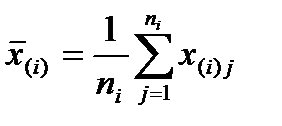 .
.
Оценка условной дисперсии 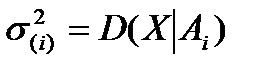 :
:
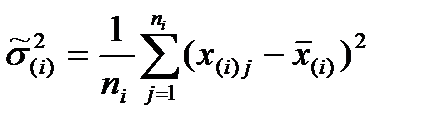 .
.
Можно показать, что справедливо тождество для суммы квадратов отклонений:

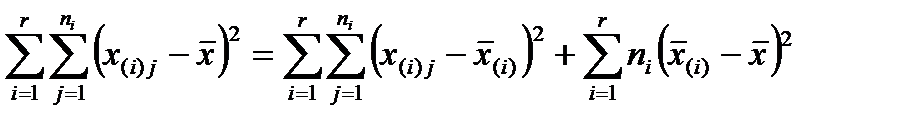 .
.
Разделив все части этого равенства на n, получим:
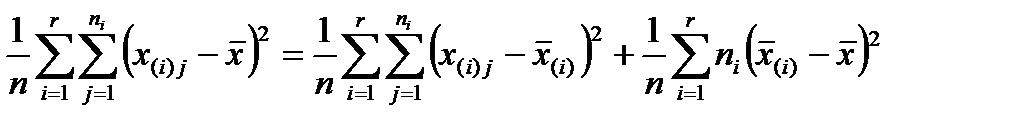 .
.
В левой части написанного равенства стоит S2 - оценка дисперсии генеральной случайной величины Х, в правой части – два слагаемых.
Второе слагаемое в правой части – это нормированная сумма квадратов между группами, которая является дисперсией групповых средних, ее называют межгрупповой дисперсией:
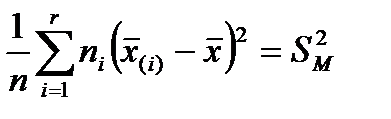 .
.
Межгрупповая дисперсия отражает влияние фактора А на генеральную случайную величину Х.
Первое слагаемое в правой части, нормированная сумма квадратов внутри групп, представляет собой среднюю из групповых дисперсий, ее называют внутригрупповая дисперсия:
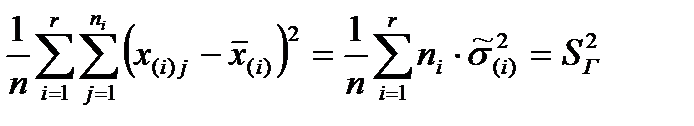 .
.
Внутригрупповая дисперсия отражает влияние остаточных факторов (не включенных в модель).
Итак, получено правило сложения дисперсий:
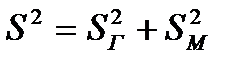
- общая дисперсия наблюдений равна сумме внутригрупповой дисперсии и межгрупповой дисперсии.
Факторный анализ – раздел корреляционного анализа, позволяющий провести отбор факторов модели.
Основной задачей корреляционного анализа является выявление статистической зависимости между случайными переменными (факторами)путём оценок различных коэффициентов корреляции.
При функциональной зависимости между величинами y=f(x), которую изучает математический анализ, каждому значению независимой переменной х соответствует определённое значение величины у.
В теории вероятностей и математической статистике изучается, как правило, стохастическая зависимость между случайными величинами, когда одному и тому значению х может соответствовать в зависимости от случая различные значения величины y. При стохастической зависимости величины не связаны функционально, но как случайные величины связаны совместным распределением вероятности.
Наличие стохастической зависимости объясняется тем, что на результирующую переменную Y действует на только контролируемый фактор Х, но и множество других неконтролируемых случайных факторов.
Корреляционной зависимостью между переменными называется функциональная зависимость между значениями одной из них и условным математическим ожиданием другой.
Корреляционная зависимость может быть представлена в виде:
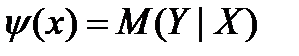 .
.
При изучении по выборке корреляционной зависимости двух случайных величин Х и Y, сначала на координатной плоскости изображают все выборочные точки 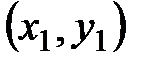 ,
, 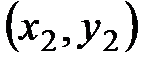 ,…,
,…, 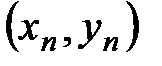 . Это изображение называют корреляционным полем.
. Это изображение называют корреляционным полем.
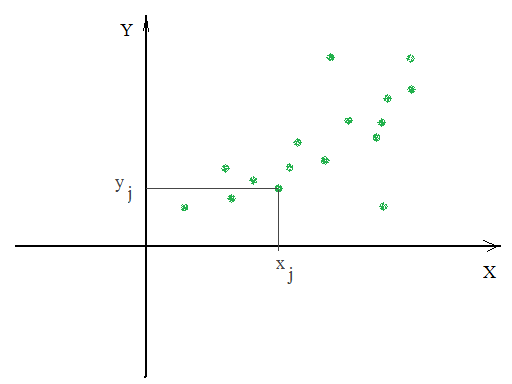
Иногда уже по виду корреляционного поля можно сделать предварительные выводы о связи между случайными переменными X и Y.
Затем составляют корреляционную таблицу:
| Возможные значения | y1 … yj … ym | Всего |
| х1 … xi … xl | n11 … n1j… n1m …………………………… ni1 … nij… nim …………………………… nl1 … nlj… nlm | n1· … ni· … nl· |
| Всего | n·1 … n·j… n·m | n |
где nij- частота, с которой пара (xi , yj) встретилась в выборке;
для непрерывных распределений в качестве xi и yj берут середины интервалов группировки.
Корреляционная таблица является основой для всех последующих вычислений.
Методы корреляционного анализа дают хорошие результаты в том случае, когда данные эксперимента можно считать выбранными из совокупности, распределённой по многомерному нормальному закону.
Дата добавления: 2018-11-25; просмотров: 1104;
