Изотермы Ван-дер-Ваальса и Эндрюса. Внутренняя энергия реального газа.

Рассмотрение явлений с энергетической, термодинамической точки зрения имеет не только чисто научное, но и большое практическое значение, так как в основе очень большого числа технических устройств лежит обмен энергией, перевод ее из одних форм в другие, получение энергии за счет совершения работы и наоборот. Законы, лежащие в основе термодинамики, носят название начал термодинамики.

С передачей энергии от одних тел к другим, с превращением энергии из одной формы в другую каждый из нас сталкивается ежедневно. Но как мы понимаем передачу энергии, например, в виде теплоты, от одного тела к другому? Для получения ответа на этот вопрос возьмем два одинаковых сосуда, наполненных одинаковым количеством воды, находящейся при одной и той же температуре Т₀. Нагреем на спиртовке или на газовой горелке свинцовый и железный стержни одной и той же массы до одной и той же температуры Т и опустим их в эти сосуды. По истечении какого-то времени мы обнаружим, что температура воды в сосудах будет разной: в сосуде, в который было погружен железный стержень, температура выше, чем во втором сосуде, в который был погружен свинцовый стержень. Этот опыт убедительно говорит о том, что железо передало воде за одно и то же время большее количество теплоты, чем свинец. Продолжая экспериментировать, мы установили бы, что воде пришлось бы передавать тем большее количество тепла ∆Q, чем больше ее масса m, т. е. ∆Q ~ m. Более того, тепла воде надо было бы передать тем больше, чем выше должно было бы быть приращение температуры, т. е. ∆Q ~ ∆Т. Обобщая, можно сказать, что количество тепла, сообщаемое телу или отнимаемое от него, пропорционально его массе и изменению его температуры, т. е.

∆Q = сm∆Т, (2.3.1)

где с – удельная теплоемкость. Из 2.3.1 легко установить, что

с = ∆Q/m∆Т, (2.3.2)

т. е. чтоудельная теплоемкость есть количество теплоты, переданное телу единичной массы (1 кг), чтобы повысить его температуру на один градус.Единицей удельной теплоемкости является Дж/кг_*К.

Кроме удельной теплоемкости, существует и молярная теплоемкость – это количество теплоты, необходимое для нагревания 1 моля вещества на 1 К,поэтому можно записать математическое определение молярной теплоемкости:

C_m =∆Q/ν∆Т, (2.3.3)

где ν = m/M, а M – молярная масса вещества. Из 2.3.3 следует, что единица измерения молярной теплоемкости – Дж/моль_*К. Сравнивая 2.3.2 и 2.3.3, получаем, что

C_m = cM. (2.3.4)

Выражения 2.3.2 и 2.3.3 подсказывают путь измерения количества теплоты. В самом деле, если нагретое тело приводится в соприкосновение, например, с водой так, чтобы теплообмен происходил только между телом и водой, то количество теплоты, переданное нагретым телом, будет равно количеству теплоты, принятому водой, т. е. будет справедливо соотношение:

∆Q = с_нтm_нт∆Т_нт = с_вm_в∆Т_в. (2.3.5)

Поскольку теплоемкости тела и воды известны, а их массы и перепады температур можно измерить, то это означает, что измерению поддается и количество теплоты ∆Q. Подобные измерения проводились очень интенсивно еще в XVIII – XIX веках. И здесь стали выявляться удивительные факты. Джоуль обнаружил, что температура тела может быть повышена как путем сообщения ему 1 калории (или 4.18 Дж) теплоты, так и за счет совершения против него внешними силами работы, равной 4.18 Дж. Было установлено, что, если работа совершается за счет тепла, взятого от какого-то тела, то за счет 1 калории этого тепла совершается работа в 4.18 Дж. Вывод об эквивалентности количества тепла и работы позволяет считать, что передача энергии от одних тел к другим может осуществляться как за счет передачи тепла (∆Q), так и за счет совершения работы (∆А).

Являясь мерой изменения энергии системы, величины ∆Q и ∆А ей не тождественны. Энергия системы является ее характеристикой и тогда, когда она не изменяется. Но в этом случае ∆Q и ∆А будут неопределенными. Они становятся определенными только тогда, когда изменяется энергия системы.

Представим себе теперь цилиндр с поршнем, наполненный газом, обладающим внутренней энергией U₁. Если газ получит некоторое количество теплоты ∆Q, он перейдет в новое состояние с внутренней энергией U₂ и совершит работу А над внешней средой (такая работа считается при анализе положительной). Каким бы ни был способ перехода системы из одного состояния в другое, в соответствии с законом сохранения энергии изменение внутренней энергии ∆U = U₂ – U₁ будет одинаковым и равным разности между количеством полученной теплоты и совершенной над внешними телами работой, т. е.

∆U = ∆Q – A или ∆Q = ∆U + A. (2.3.6)

Уравнение 2.3.6 выражает первое начало термодинамики: теплота, сообщаемая системе, расходуется на изменение ее внутренней энергии и на совершение ею работы против внешних сил.

Если система периодически возвращается в исходное состояние, то изменение ее внутренней энергии будет равно нулю. Тогда из 2.3.6 получается, что A = ∆Q. А это означает, что никакая система (например, двигатель) не может за один период совершить работу, которая была бы больше, чем сообщенная ей (ему) теплота. На этом основании говорят, что вечный двигатель первого рода невозможен (это одна из формулировок первого начала термодинамики). Более того, это означает, что при ∆Q = 0 и А = 0.

Рассмотрим процесс, при котором изменяются p, v и T определенного количества газообразного вещества.

р С₁

р

С₂

V₁ ∆ VV₂V

Рис. 2.3.1.

На диаграмме «р – V» изобразим начальное состояние точкой С₁, а конечное – точкой С₂. Если бы давление газа было постоянным, то при своем расширении (например, при нагревании) газ совершал бы работу

A = p(V₂ – V₁). (2.3.7)

В общем же случае изменяется и давление. Поэтому введем столь малое изменение объема ∆V, при котором давление р можно считать постоянным. Тогда элементарная работа ∆А, которая будет совершаться при таком изменении объема, будет равна произведению р∆V. Практически это будет площадь четырехугольника над обозначением ∆V (см. рис. 2.3.1). Для рассматриваемого нами элементарного процесса закон сохранения энергии запишется в виде:

∆Q = ∆U + р∆V. (2.3.8)

Для 1 моля вещества в соответствии с 2.3.3 ∆Q = C_m∆T. Если объем системы остается неизменным, то

∆Q = ∆U = C_v∆T = iR∆T/2, (2.3.9)

где C_V – теплоемкость при постоянном объеме. Из 2.3.9 следует, что

C_V = iR/2. (2.3.10)

Если же газ нагревается при постоянном давлении, он расширяется, поэтому 2.3.9 можно переписать в следующем виде:

С_р∆T = iR∆T/2 + р∆V, (2.3.11)

откуда для теплоемкости при постоянном давлении, С_р, выразив по уравнению Клапейрона - Менделеева объем 1 моля газа (V = RT/p), получаем:

С_р = iR/2 + р∆V/∆T = C_V + R = (i + 2)R/2. (2.3.12)

Это уравнение показывает, что теплоемкость при постоянном давлении всегда больше теплоемкости при постоянном давлении на величину универсальной газовой постоянной. Это объясняется тем, что при нагревании газа при постоянном давлении требуется дополнительное количество теплоты на совершение работы против внешних тел, так как постоянство давления обеспечивается расширением газа.

Во многих термодинамических процессах важную роль играет отношение С_р/ C_V = γ. Из 2.3.12 легко установить, что

γ = (i + 2)/i. (2.3.13)

Теперь рассмотрим, как проявляется первое начало термодинамики в изопроцессах, т. е. в процессах, в которых один из трех основных параметров состояния остается неизменным.

Изохорный процесс (V = const).В координатах «p – V» диаграмма этого процесса описывается прямой (изохора), которая параллельна оси ординат. При таком процессе газ не совершает работы над внешними телами, вся теплота идет на увеличение внутренней энергии 1 моля газа:

∆Q = ∆U = C_V∆T, (2.3.14)

а для произвольного количества газа получим

∆Q = ∆U = C_V∆Tm/M, (2.3.15)

Изобарный процесс (p = const).Диаграммой в этом процессе является прямая (изобара), параллельная оси абсцисс, а работа, совершаемая газом при его расширении, равна

A = p(V₂ – V₁), (2.3.16)

т. е. графически она представляет собой площадь прямоугольника, вертикальная сторона которого равна р, а сторона по горизонтали – разнице между V₂ и V₁.По закону Клапейрона – Менделеева pV₁ = mRT₁/M, pV₂ = mRT₂/M, поэтому

А = p(V₂ – V₁)= mR(T₂ – T₁)/M. (2.3.17)

Если T₂ – T₁ = 1 К, то для 1 моля газа R = A, т. е. по своему физическому смыслу универсальная газовая постоянная R численно равна работе изобарного расширения 1 моля идеального газа при нагревании на 1 К.

Изотермический процесс (T = const). Такой процесс подчиняется закону Бойля – Мариотта pV = const и графически описывается гиперболой, называемой изотермой. Работа изотермического расширения газа

A = 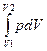= = 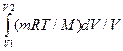(mRT/M)ln(V₂/V₁) =

= (mRT/M)ln(p₁/p₂). (2.3.18) Поскольку T = const, внутренняя энергия газа не изменяется, поэтому все количество теплоты, которое сообщается газу, идет на совершение им работы против внешних сил.

Адиабатический процесс (∆Q = 0)– это процесс, протекающий без теплообмена между газом и окружающей средой, поэтому работа газа против внешних сил может совершаться только за счет уменьшения внутренней энергии системы. Для такого процесса

pV^γ = const. (2.3.19)

Линия (гипербола), описывающая адиабатический процесс, называется адиабатой,она идет круче, чем изотерма.Показатель γ в 2.3.19 называется показателем адиабаты или коэффициентом Пуассона. Если газ расширяется от объема V₁ до V₂, то его температура уменьшается от Т₁ до Т₂, а работа адиабатического расширения газа

A = C_V(T₁ – T₂)m/M. (2.3.20)

На практике большое значение играют круговые или циклические процессы, в которых конечное и начальное состояния системы совпадают. На диаграмме состояния круговые процессы изображаются замкнутой кривой 1 – а – 2 – b – 1 (рис. 2.3.2).

р

1 a

A

b 2

V₁ V₂ V

Рис. 2.3.2.

Круговой процесс (или цикл) можно разбить на процесс расширения газа (1 → 2) и на процесс его сжатия (2 → 1). Поскольку при расширении газа изменение объема dV = V₂ – V₁ > 0, то положительной считается и совершенная газом работа против внешних тел, а при сжатии газа dV < 0, поэтому работа считается отрицательной.Если процесс расширения газа из состояния 1 в состояние 2 протекает через промежуточное состояние a, авозврат из 2 состояния в 1 проходит через промежуточное состояние b (т. е цикл совершается по часовой стрелке), то такой круговой процесс называется прямым. Из рис. 2.3.2 легко понять, что работы расширения (положительная работа) и сжатия (отрицательная работа) газа численно равны площадям геометрических фигур, ограниченных точками (состояниями) V₁-1-a-2-V₂ и V₂-2-b-1-V₁, соответственно.Это означает, что результирующая работа, совершаемая системой за 1 цикл, равна площади фигуры, охватываемой замкнутой кривой.

Прямой цикл используется в тепловых машинах (двигателях), которые совершают работу за счет теплоты, получаемой, например, от сжигания топлива. Если же цикл протекает против часовой стрелки, т. е. в направлении 1 – b – 2 – а – 1, он называется обратным. По обратному циклу работают холодильные машины, в которых за счет работы внешних сил против газа теплота переносится от тела с меньшей температурой к телу с большей.

Поскольку в круговом цикле система возвращается в исходное состояние, то изменение внутренней энергии газа за цикл равно нулю, поэтому работа, совершаемая за цикл, равна полученной извне теплоте (Q = A). Но система в круговом процессе может как получать (Q₁) теплоту, так и отдавать ее (Q₂), поэтому результирующее количество теплоты

Q = Q₁ – Q₂. (2.3.21)

Для характеристики эффективности работы системы вводится понятие термического коэффициента полезного действия кругового процесса

η = A/Q₁ = Q₁ – Q₂/Q₁ = 1 – Q₂/Q₁. (2.3.22)

Из 2.3.22 видно, что эффективность кругового процесса тем выше, чем меньше отношение Q₂/Q₁, т. е. тогда, когда Q₂ << Q₁.

Различают обратимые и необратимые термодинамические процессы. Обратимым называют такой круговой процесс, в котором после возвращения системы в исходное состояние не наблюдается никаких изменений ни в самой системе, ни в окружающей ее среде. Если же изменения имеют место, круговой процесс будет отнесен к необратимым.

В термодинамике широко пользуются понятием энтропии, которое ввел в научный обиход Р. Клаузиус. Чтобы понять, что это такое, рассмотрим тело, которое получило в изотермическом процессе некоторое количество теплоты Q от другого тела, находящегося при температуре Т. Отношение Q/T называется приведенным количеством теплоты. На бесконечно малом этапе процесса приведенное количество теплоты будет равно δQ/T, а в любом обратимом круговом процессе интеграл от δQ/T, взятый по замкнутому контуру, равен 0. Это, однако, означает, что выражение, стоящее под знаком интеграла по замкнутому контуру есть полный дифференциал некоторой функции, которая не зависит от пути, по которому система пришла в рассматриваемое состояние, а определяется только состоянием системы. Иными словами

δQ/T = dS, (2.3.23)

где S– функция состояния, называемая энтропией, дифференциалом которой является δQ/T. Для обратимых процессов ∆S = 0, для необратимых ∆S > 0. Обратимым является любой равновесный процесс. Однако обратимые процессы – это идеализация реальных процессов, поскольку практически в любом реальном процессе имеются потери энергии. Приведенные выше условия можно объединить в одно неравенство Клаузиуса

∆S ≥ 0, (2.3.24)

которое говорит о том, что энтропия замкнутой системы (т. е. системы, не обменивающейся теплотой с окружающей средой) может либо возрастать (необратимые процессы), либо оставаться неизменной (обратимые процессы).

Если система совершает равновесный переход из состояния 1 в состояние 2, то в соответствии с 2.3.23 изменение энтропии

∆S = S₂ – S₁ = 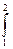δQ/T = 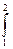(dU + δA)/T. (2.3.25)

Подставим в 2.3.25 dU = mC_VdT/M и δA = pdV, получим

∆S = S₂ – S₁ = (mC_V/M) 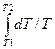+ (mR/M) =

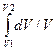= m/M[C_Vln(T₂/T₁) + Rln(V₂/V₁)]. (2.3.26)

Для адиабатического процесса δQ = 0, значит, и ∆S = 0, т. е. S = const. Иными словами, обратимый адиабатический процесс протекает при постоянной энтропии.Далее, из2.3.26следует, что при изотермическом процессе, когда T₁ = T₂, ∆S = (mR/M)ln(V₂/V₁), а при изохорном процессе, когда V₁ = V₂, ∆S = (mC_V/M)ln(T₂/T₁).

Энтропия системы равна сумме энтропий тел, входящих в нее (свойство аддитивности).

В статистической физике

S = klnW, (2.3.27)

где k – постоянная Больцмана, а W – число способов, которыми может быть реализовано то или иное макроскопическое состояние системы. Энтропию можно рассматривать как меру вероятности реализации такого макросостояния. Кроме того, энтропию можно рассматривать и как меру неупорядоченности системы. Энтропия максимальна в состоянии равновесия системы, поскольку число способов его достижения максимально.

Первое начало термодинамики, как мы видели, выражает закон сохранения и превращения энергии. Однако оно не дает никакого ответа на вопрос о направлении того или иного процесса. Ответ на него дает второе начало термодинамики, которое является законом возрастания энтропии в замкнутой системе: любые необратимые процессы в замкнутой системе происходят так, что энтропия системы возрастает. В свою очередь возрастание энтропии в замкнутой системе при необратимых процессах означает переход системы из менее вероятных в более вероятные состояния.

Существуют еще две формулировки второго начала термодинамики:

1). по Кельвину: невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу;

2). по Клаузиусу: невозможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к более нагретому.

Первое и второе начала термодинамики дополняются третьим началом или теоремой Нернста – Планка: энтропия всех тел в состоянии равновесия стремится к нулю по мере приближения температуры к 0 К. Это означает, что при 0 К теплоемкости C_p и C_V равны нулю.

Рассмотрим круговой процесс, который впервые рассмотрел Карно и который получил название цикла Карно. Цикл Карно – это обратимый процесс, состоящий из двух изотерм и двух адиабат (рис. 2.3.3) и совершаемый в направлении 1 → 2 → 3 → 4 → 1.

р

1(p₁, V₀₁) изотерма (T₁, Q₁)

2(p₂, V₀₂)

адиабата

4(p₄, V₀₄) адиабата

3(p₃, V₀₃)

изотерма (T₂, Q₂)

V

Рис. 2.3.3.

Для его осуществления надо иметь нагреватель, который сообщает газу определенное количество теплоты при его изотермическом расширении, и холодильник, принимающий от газа соответствующее количество теплоты при его изотермическом сжатии. Предположим, что в качестве рабочего газа используется идеальный газ, который находится в состоянии 1, характеризуемом давлением p₁, объемом V₀₁ и температурой T₁. Заставим газ изотермически расширяться, сообщив ему от нагревателя количество теплоты Q₁. Расширяясь до объема V₀₂, газ совершит работу A₁ = Q₁. Из состояния 2 дадим газу возможность адиабатически расширяться до состояния 3, которое характеризуется давлением p₃, объемом V₀₃. При таком расширении газ охладится до температуры T₂. Из состояния 3 будем газ сжимать изотермически при температуре T₂ до состояния 4, характеризуемого объемом V₀₄ и давлением p₄. При таком изотермическом сжатии газ отдаст холодильнику количество теплоты Q₂ и совершит работу A = – Q₂. Наконец, сожмем газ адиабатически до объема V₀₁, его давление примет значение р₁, а температура повысится до температуры Т₁.

Коэффициент полезного действия такого кругового процесса

η = A/Q₁ = (Q₁ – Q₂)/Q₁, (2.3.28)

где А – суммарная работа. Использовав выражения для работы при изотермическом и адиабатическом процессах, получим, что

η = ( Т₁ – Т₂)/Т₁. (2.3.29)

Отметим, что цикл Карно представляет собой идеальную тепловую машину. Из 2.3.29 следует, что η = 1 только при Т₂ = 0 К. Реально η всегда меньше единицы. Если цикл Карно провести в обратном направлении, он явится идеальной холодильной машиной.

Модель идеального газа достаточно хорошо описывает поведение реальных газов только при достаточно высоких температурах и низких давлениях, когда размерами самих молекул можно пренебречь. Если, однако, давление растет, то средние расстояния между молекулами уменьшаются, поэтому необходимо принимать во внимание объем молекул и взаимодействие между ними. При нормальных условиях собственный объем молекул, находящихся в 1 м³ газа, составляет 0.01 %, тогда как при 500 МПа – уже 50 %. Это означает, что при высоких давлениях и низких температурах модель идеального газа не может описать поведение реальных газов. Чтобы это стало возможно, надо учесть силы межмолекулярного взаимодействия, которые проявляются на расстояниях, меньших 1 нм, и которые быстро убывают с расстоянием, из-за чего их называют короткодействующими. Это одновременно и силы притяженияF_п(считаются отрицательными), и силы отталкиванияF_о (считаются положительными), у которых разная зависимость от расстояния (рис. 2.3.4).

На расстоянии r₀ силы отталкивания и притяжения компенсируют друг друга, при r < r₀ преобладают силы отталкивания, а при r > r₀ – силы притяжения, при r > 10^-9 м силы межмолекулярного взаимодействия практически отсутствуют (рис. 2.3.4, а). Элементарная работа силы F при изменении расстояния между молекулами совершается за счет уменьшения внутренней (потенциальной) энергии газа (δA = Fdr = –dП).Эта энергия при r > 10^-9 м равна нулю (раз сила F = 0), по мере уменьшения расстояния между молекулами между ними начинают действовать силы притяжения (F < 0), которые совершают положительную работу, соответственно, потенциальная энергия системы уменьшается, при r = r₀ потенциальная энергия достигает минимума П_мин (наиболее устойчивое состояние), а при дальнейшем уменьшении расстояния начинают преобладать силы отталкивания, и потенциальная энергия резко возрастает (рис. 2.3.4,б).

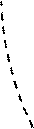
F F_о

а) F

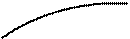
r₀ r, м

F_п

П

б) r, м

П_мин

Рис. 2.3.4.

Учет собственного объема молекул был проделан Ван-дер-Ваальсом за счет введения поправок в уравнение Клапейрона – Менделеева. Раз между молекулами на малых расстояниях действуют силы отталкивания, которые не дают другим молекулам проникать в объем, занятый каким-то количеством газа, то это означает, что объем, в котором могут двигаться молекулы, равен не V_m, а V_m – b, где b – собственный объем молекул. Далее, действие сил взаимного притяжения молекул приводит к появлению так называемого внутреннего давления на газ. Ван-дер-Ваальс вычислил, что оно обратно пропорционально квадрату молярного объема V_m, т. е.

p’ = a/V_m², (2.3.30)

где а – постоянная Ван-дер-Ваальса. Если ввести эти поправки в уравнение Клапейрона – Менделеева, оно для 1 моля газа примет вид

(p + a/V_m²)(V_m – b) = RT. (2.3.31)

При высоких температурах изотерма Ван-дер-Ваальса представляет собой монотонно спадающую кривую, почти не отличающуюся от изотермы Бойля – Мариотта. Однако при некоторой температуре у изотермы появляется точка перегиба (критическая точка К на рис. 2.3.5), изотерма для этой температуры называется критической, а соответствующие ей температура, объем и давление – критическими температурой(T_к), объемом (V_к) и давлением (р_к). В целом система, находящаяся при таких критических параметрах, называется критическим состоянием. При дальнейшем понижении температуры изотермы демонстрируют волнообразный участок, на котором по мере увеличения объема, занимаемого газом, изотерма сначала опускается вниз, затем поднимается вверх (это означает, что давление в системе растет по мере увеличения объема, что представляется невозможным) и после этого снова монотонно спускается вниз.

Если Ван-дер-Ваальс изучал поведение реальных газовых систем теоретически, то Эндрюс экспериментально определил ход изотерм для углекислого газа. Теоретически и экспериментально полученные изотермы отличаются друг от друга тем, что Эндрюс не обнаружил волнообразного хода изотерм, вместо волны 1-2-3-4-5-6-7 его изотермы 1-2-6-7 демонстрировали горизонтальный участок 2-6. Одна из причин такого различия состоит в том, что при уменьшении объема вещество переходит из газообразного состояния (когда объем системы большой) в жидкое (объем маленький). Горизонтальный участок изотерм Эндрюса отвечает равновесию между жидкой и газообразной фазой вещества. Вещество в газообразном состоянии при температуре ниже критической называется паром, а пар, находящийся в равновесии со своей жидкостью, – насыщенным. Решение уравнения Ван-дер-Ваальса дает следующие значения критических параметров:

V_к =3b, p_к = a/(27b²), T_к = 8a/(27Rb). (2.3.32)

Рис. 2.3.5

Как говорилось ранее, внутренняя энергия идеального газа, молекулы которого не взаимодействуют друг с другом, пропорциональна только температуре газа. В случае же реального газа нужно еще учесть потенциальную энергию межмолекулярного взаимодействия молекул, которая обусловлена только силами притяжения молекул друг к другу. Чтобы преодолеть эти силы притяжения, необходимо совершить определенную работу. Поэтому полная энергия реального газа

U_m = C_VT – a/V_m (2.3.33)

растет с температурой (как и в случае идеального газа) и с увеличением объема (когда взаимное притяжение сходит на нет). Если газ расширяется адиабатически и не совершает никакой работы против внешней среды, то внутренняя энергия газа не изменяется, т. е. U₁ = U₂. В случае идеального газа это означает и равенство температур Т₁ и Т₂. А что будет для реального газа? Для 1 моля газа можно записать уравнения для двух состояний газа

U₁ = C_VT₁ – a/V₁; U₂ = CT₂ – a/V₂, (2.3.34)

откуда легко получить следующее уравнение

T₁ – T₂ = (1/V₁ – 1/V₂)a/C_V. (2.2.35)

Из этого уравнения следует, что реальный газ при адиабатическом расширении в вакуум охлаждается, а при адиабатическом сжатии – нагревается.

Контрольные вопросы

1. Что понимают под началами термодинамики? Сколько их?

2. Каков физический смысл удельной и молярной теплоемкостей?

3. Как соотносятся друг с другом теплота, подводимая к газу, и работа, совершаемая против него внешними силами.

4. Как формулируется первое начало термодинамики?

5. Почему невозможен вечный двигатель первого рода?

6. Как связаны друг с другом теплоемкости при постоянном давлении и постоянном объеме?

7. Как вычислить работу при изобарном процессе?

8. За счет чего совершается работа при изотермическом и адиабатическом процессах?

9. Чему равна работа при изохорном процессе?

10. Какими кривыми описываются изотерма и адиабата и как они выглядят в координатах «p – V»?

11. Какой процесс называется круговым? В чем разница между обратимым и необратимым процессом?

12. Что такое термический коэффициент полезного действия кругового процесса?

13. В чем суть неравенства Клаузиуса для энтропии замкнутой системы? Как формулируется второе начало термодинамики?

14. О чем говорит третье начало термодинамики?

15. Что такое цикл Карно и как он реализуется?

16. Какие силы действуют между молекулами газа при больших давлениях?

17. В чем отличие изотерм для идеального и реального газов?