Свойства свободного гироскопа.
На предыдущих лекциях мы в основном говорили о поступательном движении. Вместе с тем и в повседневной жизни, и в практической деятельности мы постоянно сталкиваемся с телами, которые совершают вращение вокруг какой-то оси. При изучении вращения твердого тела широко пользуются понятием момента инерции. Моментом инерции тела (системы тел) J относительно оси вращения называется произведение массы тела (сумма произведений масс тел) на квадрат расстояния (на квадраты расстояний) до оси:
J= 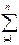 miri2. (1.4.1)
miri2. (1.4.1)
Если речь идет о непрерывном распределении масс в однородном теле, эта сумма сводится к интегралу по всему его объему
J = 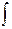 r2dm. (4.2)
r2dm. (4.2)
Значения моментов инерции для тел разной конфигурации приведены в таблице 1.4.1.
Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой оси, параллельной первой, определяется теоремой Штейнера: момент инерции тела J относительно любой оси вращения равен моменту его инерции JС относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы m тела на квадрат расстояния а между осями:
J = JС + ma2. (1.4.3)
Таблица 1.4.1.
| Тело | Положение оси вращения | Момент инерции |
| Полный тонкостенный цилиндр радиусом R | Ось симметрии | mR2 |
| Сплошной цилиндр или диск радиусом R | Ось симметрии | mR2/2 |
| Прямой тонкий стержень длиной l | Ось перпендикулярна стержню и проходит через его середину | ml2/12 |
| Прямой тонкий стержень длиной l | Ось перпендикулярна стержню и проходит через его конец | ml2/3 |
| Шар радиусом R | Ось проходит через центр шара | 2mR2/5 |
Коль скоро вращение представляет собой один из распространенных видов движения, возникает вопрос о кинетической энергии вращения. Чтобы найти, чему она равна, представим себе тело, которое вращается вокруг оси z, проходящей через него. Мысленно разобьем это тело на n малых объемов с элементарными массами mi, находящихся на расстояниях ri от оси вращения. При вращении каждый элементарный объем будет описывать окружности разных радиусов, двигаясь с разными скоростями vi, но угловая скорость ω их вращения будет одной и той же:
ω = v1/r1 = v2/r2 = … = vn/rn. (1.4.4)
Кинетическая энергия вращения твердого тела может быть получена как сумма кинетических энергий элементарных объемов:
Твр = m1v12/2 + m2v22/2 + … +mnvn2/2. (1.4.5)
Поскольку vi = ωri, то 4.5 можно переписать в следующем виде:
Твр = m1ω2ri2/2 + m2ω2r22/2 + … + mnω2rn2/2 =
=(ω2/2) 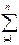 miri2 = Jzω2/2, (1.4.6)
miri2 = Jzω2/2, (1.4.6)
где Jz – момент инерции тела относительно оси z. Таким образом, кинетическая энергия вращающегося тела Твр = Jzω2/2, а кинетическая энергия движущегося поступательно тела T = mv2/2. Как видим, эти два выражения похожи друг на друга. И если m есть мера инертности тела при поступательном движении, то мерой инертности тела при вращательном движении является момент инерции.
Если, например, цилиндр будет скатываться по наклонной плоскости без скольжения, то его кинетическая энергия будет складываться из двух частей, т. е. из энергии поступательного движения и энергии вращения:
T = mvC2/2 + JCω2/2, (1.4.7)
где m – масса катящегося тела, vC – скорость центра масс тела, JC – момент инерции тела относительно оси, проходящей через его центр масс, ω – угловая скорость вращения тела.
Следующей важной характеристикой вращательного движения является момент силы. Различают момент силы относительно неподвижной точки О и момент силы относительно неподвижной оси z. Момент силы относительно точки О это физическая величина, равная векторному произведению радиус-вектора r, проведенного из 


 точки О в точку А приложения силы, на силу F (рис. 1.4.1).
точки О в точку А приложения силы, на силу F (рис. 1.4.1).
M
O
R F
l A α
Рис. 1.4.1
Вектор (точнее псевдовектор) M = [rF], онперпендикулярен плоскости, образуемой векторами r и F, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к F. Модуль момента силы
M = Frsinα = Fl, (1.4.8)
где α –угол между r и F, rsinα = l – кратчайшее расстояние от линии действия силы до точки О, которое называется плечом силы.
Моментом силы относительно неподвижной оси z называется скалярная величина Mz, равная проекции на эту ось вектора М момента силы, определенного относительно произвольной точки О, лежащей на оси z. Если ось z совпадает с направлением вектора М, то момент силы представляется в виде вектора, совпадающего с осью:
Mz = [rF]z. (1.4.9)
А чему будет равна работа при вращении тела? Пусть сила F приложена в точке В, находящейся от оси вращения на расстоянии r, а α – угол между направлением силы и радиус-вектором r. При повороте тела на бесконечно малый угол φ точка приложения силы проходит путь dS = rdφ, тогда работа будет рана произведению величины смещения на проекцию силы на направление смещения
dA = Fsinα rdφ = Mzdφ, (1.4.10)
где Frsinα = Fl = Mz – момент силы относительно оси z.
Работа при вращении тела идет на увеличение его кинетической энергии, т. е. dA = dT = d(Jzω2/2) = Jzωdω. (1.4.11)
Иными словами
Mzdφ = Jzωdω (1.4.12)
или
Mzdφ/dt = Jzωdω/dt. (1.4.13)
Учитывая, что ω = dφ/dt, после сокращения обеих частей 1.4.13 на ω, получаем
Mz = Jzdω/dt = Jzε. (1.4.14)
Выведенное нами уравнение 1.4.14 представляет собой уравнение динамики вращательного движения твердого тела относительно неподвижной оси: момент силы равен произведению момента инерции тела (меры инертности при вращении) на угловое ускорение. Как видим, этот закон похож на закон динамики поступательного движения с той лишь разницей, что во втором мы имеем дело с массой тела (мерой инертности при поступательном движении) и линейным ускорением.
Если наблюдается такая аналогия, возникает вопрос о том, какая же физическая величина при вращательном движении будет аналогом импульса тела. Оказывается, этой величиной является момент импульса относительно оси. Но сначала введем понятие момента импульса (количества движения) тела (материальной точки) относительно неподвижной точки О, под которым понимают физическую величину, определяемую векторным произведением
L = [rP] = [rmV], (1.4.15)
 uде r – радиус-вектор, проведенный из точки О в точку А; Р = mV – импульс; L –псевдовектор, направление которого совпадает с направлением поступательного движения правого винта при его вращении от r к P (рис. 1.4.2).
uде r – радиус-вектор, проведенный из точки О в точку А; Р = mV – импульс; L –псевдовектор, направление которого совпадает с направлением поступательного движения правого винта при его вращении от r к P (рис. 1.4.2).
L
 |

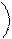
 O r A P
O r A P
l α
Рис. 1.4.2.
Модуль вектора момента импульса
L = rPsinα = mVrsinα = Pl, (1.4.16)
где α – уголмежду векторами r и P, l – кратчайшее расстояние от точки О до направления вектора Р (плечо вектора Р относительно точки О).
Моментом импульса относительно неподвижной оси z называется скалярная величина Lz, равная проекции на эту ось вектора момента количества движения (момента импульса), определенного относительно произвольной точки О, лежащей на этой оси. Отметим, что значение Lz не зависит от положения точки О на оси z.
Понятно, что при вращении твердого тела относительно неподвижной оси z каждая точка тела движется со скоростью Vi по окружности постоянного радиуса ri. Скорость Vi и момент miVi перпендикулярны этому радиусу, поэтому для отдельной частицы тела момент импульса будет равен
Liz = miViri (1.4.17)
и направлен по оси в сторону, которая определяется по правилу правого винта.
Момент импульса твердого тела относительно оси равен сумме моментов импульса его отдельных частиц
Lz = 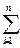 miViri. (1.4.18)
miViri. (1.4.18)
Поскольку Vi = ωri, 1.4.18 можно переписать в следующем виде
Lz = 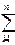 miri2ω = ω
miri2ω = ω 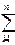 miri2 = Jzω (1.4.19)
miri2 = Jzω (1.4.19)
или
Lz = Jzω. (1.4.20)
Итак, момент импульса твердого тела относительно неподвижной оси равен произведению момента инерции тела относительно той же оси на угловую скорость.
Продифференцируем уравнение 1.4.20 по времени
dLz/dt = Jzdω/dt = Jzε = Mz, (1.4.21)
Это уравнение является еще одной формой записи уравнения динамики вращательного движения твердого тела относительно неподвижной оси. В общем виде справедливо векторное равенство
dL/dt = M. (1.4.22)
В замкнутой системе момент внешних сил равен нулю, значит, производная dL/dt = 0, а это означает, что
L = const. (1.4.23)
Уравнение 1.4.23 является законом сохранения момента импульса в замкнутой системе. Опять аналогия с поступательным движением.
Для закрепления материала сведем в одну таблицу величины и уравнения вращательного движения вокруг неподвижной оси аналогичные величины и уравнения поступательного движения (табл. 1.4.2).
Таблица 1.4.2
| Поступательное движение | Вращательное движение |
| Масса m Скорость V = dr/dt Ускорение a = dV/dt Сила F Импульс P = mV Основное уравнение динамики F = ma Работа dA = FsdS Кинетическая энергия mV2/2 | Момент инерции J Угловая скорость ω = dφ/dt Угловое ускорение ε = dω/dt Момент силы Mz или M Момент импульса Lz = Jzω Основное уравнение динамики Mz = Jzε M = dL/dt Работа Mzdφ Кинетическая энергия Jzω2/2 |
Установлено, что существуют такие оси вращения тел, которые не изменяют своей ориентации в пространстве, если на них не действуют внешние силы. Такие оси называются свободными осями. Это свойство свободных осей широко используется в технике, например, в гироскопах – массивных однородных телах, вращающихся с большой угловой скоростью вокруг своей оси симметрии, которая является свободной осью. Если момент внешних сил относительно закрепленного центра масс гироскопа равен нулю, то момент импульса L = const, это означает, что момент импульса сохраняет свою величину и направление в пространстве, а значит, сохраняет свое положение в пространстве и ось гироскопа. Чтобы она изменила свое положение в пространстве, необходимо приложить к ее концам момент внешних сил.
Гироскопы применяются в приборах навигации (гирокомпас, гирогоризонт), в устройствах поддержания заданного направления движения судна (авторулевой) или самолета (автопилот). При всяком отклонении судна или самолета от курса (сильная волна, сильный ветер) положение оси гироскопа в пространстве не изменяется. Но тогда это означает, что судно или самолет поворачиваются относительно оси гироскопа, вследствие чего включаются рули управления, возвращающие транспортное средство на заданный курс. Французский физик Ж. Фуко применил гироскоп для доказательства вращения Земли. Гироскопический эффект используется в нарезном стрелковом и артиллерийском оружии. Винтовые нарезы в стволе сообщают вылетевшему снаряду (пуле) быстрое вращение вокруг собственной оси и превращают его в гироскоп с большим моментом количества движения, из-за чего момент сил, возникающий из-за сопротивления воздуха, не опрокидывает снаряд, а лишь вызывает его прецессию вокруг направления касательной к траектории.
Контрольные вопросы
1. Что такое момент инерции вращающегося тела?
2. Как формулируется теорема Штейнера?
3. Как вычислить кинетическую энергию вращающегося тела?
4. Что такое момент силы?
5. Как найти работу вращающегося тела?
6. Как формулируется основной закон динамики вращательного движения твердого тела?
7. Что такое момент импульса вращающегося тела?
8. Как формулируется закон изменения и сохранения момента импульса?
9. Что такое гироскоп и где он применяется?
10. Как соотносятся друг с другом основные физические величины и уравнения поступательного и вращательного видов движения?
| <== предыдущая лекция | | | следующая лекция ==> |
| Ввод химических реагентов | | | Сравнительный подход |
Дата добавления: 2018-09-24; просмотров: 684;
