Двумерное температурное поле

Условия теплообмена на притолоках простенков, в наружных углах зданий и в местах примыкания к наружным ограждениям поперечных стен или перегородок искажают одномерное температурное поле, изотермы утрачивают параллельность, а поток тепла одномерность.

При теплотехнических расчетах достаточно исследовать температурное поле в двух измерениях х и у, а в направлении z (обычно принимается не менее 1 м) принять температуру постоянной, т.е. рассматривать температурное поле в плане или разрезе. Такое поле является плоским. На рис. 5.2 показан пример температурного поля в наружном углу.

Рис. 5.2 – Пример плоского температурного поля в наружном углу

В однородной материальной среде температурное поле описывается уравнением

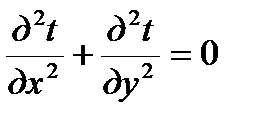. (5.6)

В неоднородной материальной среде уравнение имеет вид

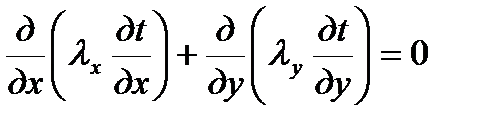. (5.7)

Здесь λ является непрерывной функцией координат х и у.

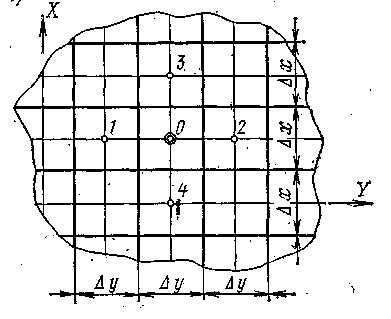
В практических расчетах используется метод конечных разностей, дающий возможность заменить непрерывное значение λ скачкообразным. Применение этого метода связано с нанесением на рассматриваемую проекцию конструкции расчетной сетки, что позволяет вычислить температуры в ее узлах. Сетка выбирается как правило квадратной со стороной Δ. Желательно, чтобы узлы сетки совпадали с поверхностями. Чем меньше величина Δ, тем точнее расчет.

Расчет состоит в определении температуры (t_xy) в точке через значения температур, окружающих эту точку со значениями температур (t₁, t₂, t₃, t₄). Эта точка обменивается с ними следующими количествами тепла:

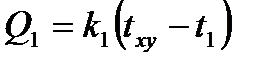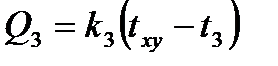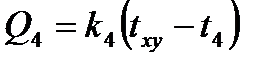; ; ; . (5.8)

Из условий теплового баланса сумма этих количеств тепла равна 0, т.е.

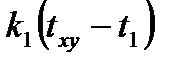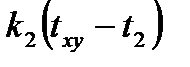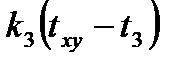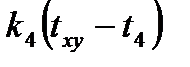+ + + = 0. (5.9)

Отсюда определяется температура в расчетной точке

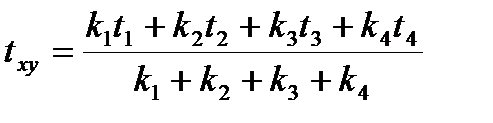, (5.10)

где k₁, k₂, k₃, k₄ - коэффициенты теплопередачи в направлении соответствующих точек. Если конструкция однородна, то расчет ведется по формуле

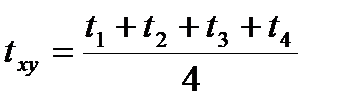. (5.11)

Коэффициент теплопередаче определяется исходя из условия, что передача теплоты происходит по квадрату abcd со стороной Δ. На рис. 5.3 показана теплопередача между t₁ и t_xy, аналогично передается тепло к другим точкам.

Рис. 5.3 – Схема передачи тепла между узлами сетки

Если материал в пределах квадрата abcd однороден, то 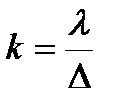, при наличии двух материалов 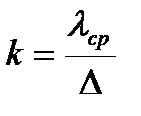( 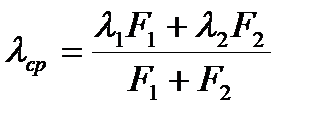- осредненный по площадям F₁ и F₂ коэффициент теплопроводности).

Если материал неоднороден, то принимается .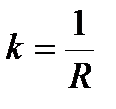

Коэффициент теплоотдачи между узлами, которые лежат на поверхности, граничащей с воздухом находится как 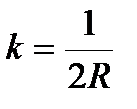, поскольку передача тепла происходит только по 0,5Δ.

Для углов наружных стен (при R_o в пределах от 0,5 до 2,5 м²К/Вт, [1]) применима эмпирическая зависимость

. (5.12)

Температура в углу может быть меньше на 2 – 6 ^оС от температуры на поверхности вдали от угла. Существуют конструктивные меры (см. рис. 5.4), способствующие увеличению температуры в углу.

Рис. 5.4 – Способы утепления наружного угла

По результатам расчета температурного поля при заданных t_В и t_Н находятся средние температуры на внутренней (t_в.ср) и наружной (t_н.ср) поверхностях ограждающей конструкции и рассчитывается величина теплового потока q^расч, Вт/м², по формуле

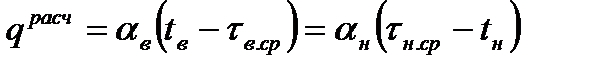, (5.13)

Приведенное термическое сопротивление конструкции находится по формуле

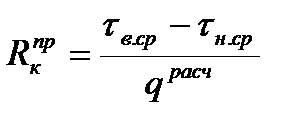. (5.14)

Приведенное сопротивление теплопередаче, R_о, м²×К/Вт, неоднородной ограждающей конструкции следует определять по формуле

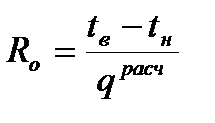. (5.15)