Теплофизические свойства строительных материалов

Знание теплофизических свойств строительных материалов позволяет эффективно использовать их для обеспечения теплозащитных качеств ограждений. Величины теплотехнических показателей строительных материалов определяются экспериментально, основные значения приведены в ДБН В.2.6-31 [1].

Плотность (объемная масса) ρ, кг/м³, представляет отношение массы вещества (т, кг) к объему вещества (V, м³) , т.е.

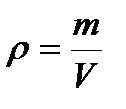. (2.1)

Пористость. Строительные материалы содержат некоторое количество пор разных размеров. Пористость, Р, выражается в % и указывает объем, занимаемый порами по отношению к общему объему.

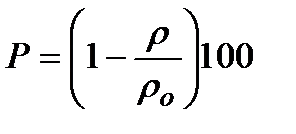, (2.2)

где ρ – плотность материала с учетом пор, ρ_о – то же только твердой части (без пор).

Влажность. Представляется содержанием в материале химически свободной воды по массе

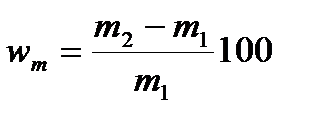или по объему 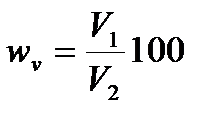, (2.3)

где т₁ и т₂ – масса сухого и влажного материала; V₁ и V₂ – объем влаги в материале и объем сухого материала, м³.

Теплопроводность. Передача тепла в материале осуществляется теплопроводностью через твердые частицы, так и теплопроводностью, конвекцией и излучением между стенками пор. Характеризуется коэффициентом теплопроводности (λ), Вт/(м∙^оС) или Вт/(м∙К). В расчетах принимается коэффициент теплопроводностикак осредненный, учитывающий все виды теплоперехода. Основное влияние на теплопроводность оказывают тепловые колебания атомов. Чем тяжелее атомы или атомные группы и слабее они между собой связаны, тем меньше теплопроводность материала. Наименьшим значение λ у воздуха (0,023), наибольшее у меди (407).

Величина коэффициента теплопроводности на основании экспериментальных исследований устанавливаются зависимостью между количеством проводимого тепла (Q, Дж), площадью (F, м²) и толщиной исследуемого материала (δ, м), временем замера (τ, с) и создаваемом при этом перепаде температур (Δ t, ^оС)следующим образом

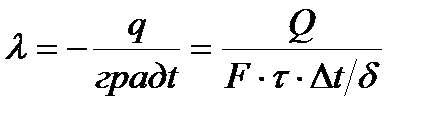= Дж/(м²∙с∙^оС/м) = Вт/(м∙^оС). (2.4)

Коэффициент теплопроводности в свою очередь зависит от:

- плотности и пористости материала. Т.к. теплопроводность воздуха меньше теплопроводности любых материалов, то повышение пористости приводит к уменьшению коэффициента теплопроводности. Особенно благоприятны мелкие поры. В крупных порах выше определенного предела происходит рост λ из-за возникновения конвективных токов. Чем плотнее материал, тем больше величина λ;

- влажности. Поры заполняются влагой и замена воздуха на воду способствует увеличению λ. Коэффициент теплопроводности влажного материала по отношению к сухому с λ_о, определяется условно линейной зависимостью

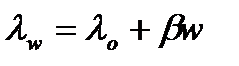. (2.5)

Здесь β коэффициент, зависящий от материала (керамзитобетон β = 0,105, пенобетон β = 0,011 и т.п.). Условия эксплуатации конструкции (характеристики микроклимата и окружающей среды) также накладывают отпечаток на теплофизические характеристики материала, В инженерных расчетах это учитывается т.н. режимом эксплуатации (“А” иди” Б”, определяемых по ДБН В.2.6-31 [1]);

- температуры. В общем виде наблюдается линейный закон роста коэффициента теплопроводности в виде

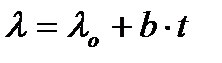. (2.6)

Здесь λ_о коэффициент теплопроводности при 0 ^оС; b – коэффициент, величина которого колеблется в пределах 0,0001 – 0,001 и зависит от вида материала (принимается по таблицам Б.Н. Кауфмана, исключение составляют магнезиальный кирпич и металлы и их соединения, кроме алюминия и латуни). В строительной практике обычных зданий этой зависимостью пренебрегают, она учитывается только при теплоизоляции оборудования с очень низкими или высокими температурами;

- анизотропности – неравномерности теплопроводности в различных направлениях. Этим свойством обладают большинство слоистых материалов и, особенно, древесина. Так у дуба поперек волокон λ практически вдвое меньше, чем у дуба вдоль волокон.

Теплоемкость – способность материалов поглощать (отдавать) тепло при повышении (понижении) температуры окружающего воздуха. Характеризуется массовой теплоемкостью материала (с, кДж/кг∙^оС), которая зависит от удельной теплоемкости (с_о) и влажности материал (w, %). Приближенно зависимость имеет вид

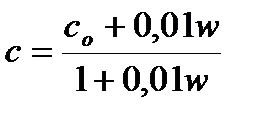. (2.7)

Часто при решениях линейных уравнений используется понятие объемной плотности сρ. В случаях постоянных значений λ и сρ вводится понятие коэффициента температуропроводности (а, м²/с), являющегося отношением указанных величин и равным .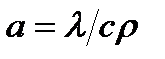

Виды теплопередачи

Теплопроводность

Теплопроводность это теплообмен между частицами или элементами структуры материальной среды, находящимися в непосредственном соприкосновении друг с другом. Передача тепла происходит от более теплых слоев (поверхностей) к холодным. В теории теплопроводности пренебрегают (виду малости частиц и расстояний между ними) корпускулярным строением вещества, считая его сплошной средой.

Количество тепла при неизменном температурном перепаде (стационарный тепловой поток), проходящее через единицу площади согласно уравнения Фурье составит

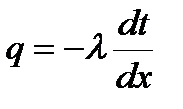, (2.8)

где 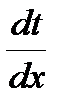- изменение (градиент) температур по толщине в направлении х.

Знак (-) в формуле показывает, что тепловой поток направлен в сторону понижения температуры.

При неустановившихся условиях (нестационарный поток) количество тепла, распространяющееся в направлении х изменяется, что связано с поглощением и отдачей тепла частицами материальной среды при изменении температуры с течением времени. В таком случае изменение потока находится дифференцированием предыдущего выражения

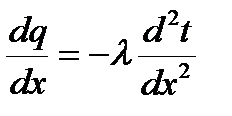. (2.9)

Изменение потока тепла пропорционально теплоемкости материала сρ и может быть выражено зависимостью

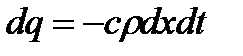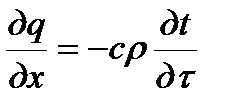или (2.10)

При отсутствии внутренних источников и стоков тепла изменение величины теплового потока связано только с поглощением тепла материалом и потому последние два выражения (3.9 и 3.10) равны между собой

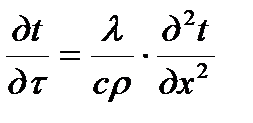. (2.11)

При неустановившемся распространении тепла по всем трем осям координат дифференциальное уравнение приобретает вид:

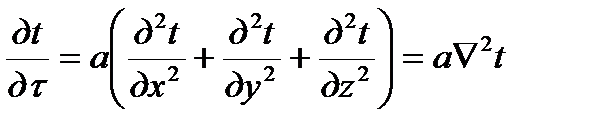, (2.12)

где 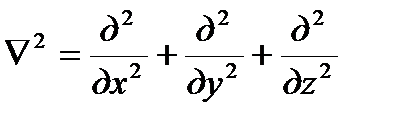- оператор Лапласа.

В стационарных условиях теплопередачи изменение температуры во времени не происходит ( 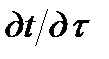), тогда уравнение Лапласа имеет вид

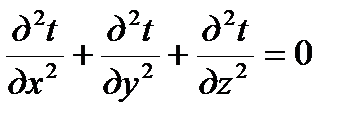. (2.13)

При двумерном распространении тепла уравнение выглядит

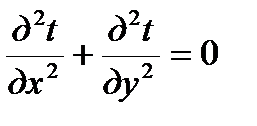. (2.14)

Для одномерного распределения тепла

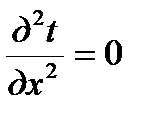. (2.15)

Конвекция

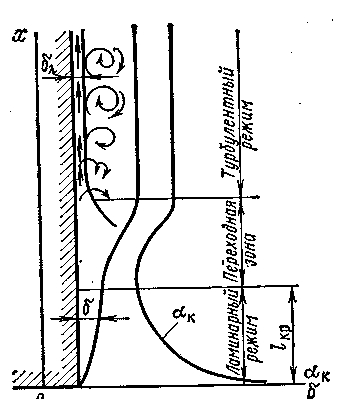
Конвекция – теплообмен движущимися массами воздуха у нагретых или охлажденных поверхностей. У нагретых воздух [2] поднимается вверх, а у холодных опускается вниз. В потоке около вертикальной поверхности образуется пограничный слой, толщина которого (см. рис. 2.1) возрастает по направлению движения. В инженерных расчетах принимается свободная конвекция за счет естественных сил.

По высоте можно выделить три условных зоны. У пола располагается зона ламинарного потока. Длина этой зоны (при температуре внутреннего воздуха 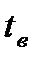= 20 ^оС) равна 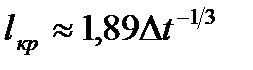. Среднее значение коэффициента конвективного обмена в пределах этой зоны составляет 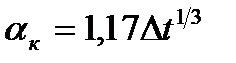. Здесь 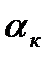- коэффициент конвективного теплообмена, равный тепловому потоку, приходящемуся на единицу поверхности в единицу времени при разности температур между воздухом и поверхностью 1 ^оС.

Затем происходит нарушение ламинарного течения, в переходной зоне появляются поперечные движения воздуха. В третьей по высоте зоне устанавливается турбулентный режим. Для турбулентной зоны коэффициент конвективного теплообмена не зависит от высоты и его величина определяется как .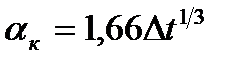

Рис. 2.1 – Пограничные слои при свободной конвекции ( 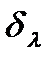- толщина ламинарного подслоя) [2]

Для горизонтальной поверхности закон распределения тот же, но меняются численные коэффициенты:

горизонтальная, обращенная вверх нагретая - 2,26, охлажденная – 1,16;

горизонтальная, обращенная вниз нагретая – 1,16, охлажденная – 2,26.

В случае, если поверхность горячая обращена вверх или холодная поверхность вниз, то наблюдается “сахар-эффект”. Воздух (см. рис. 2.2а) опускается про границам шестигранников и поднимается в их центрах. За счет сложностей подвода воздуха к центральной части при увеличении размеров горизонтальной поверхности средний коэффициент 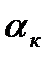уменьшается.

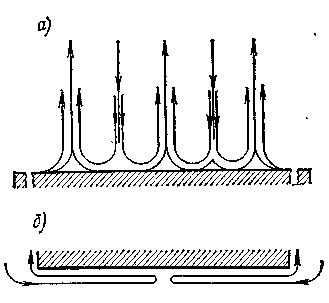
Рис. 2.2 – Движение воздуха при свободной конвекции около горизонтальной нагретой поверхности, обращенной нагретой стороной вверх (а) и вниз (б) [2]

У горизонтальной поверхности, обращенной вниз или холодной, обращенной вверх движение воздуха происходит по схеме, представленной на рис. 2.2.б

Здесь также с увеличением площади поверхности осложняется подвод тепла и среднее значение 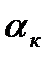уменьшается.

В инженерных расчетах для определения количества тепла Q_к, Вт, используется формула Ньютона

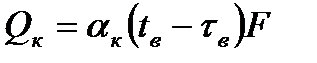, (2.16)