Десятичные кратные и дольные единицы
| Множитель | Наименование приставки | Обозначение приставки | Множитель | Наименование приставки | Обозначение приставки |
| 1018 | Экса | Э | 10-1 | Деци | д |
| 1015 | Пета | П | 10-2 | Санти | с |
| 1012 | Тера | Т | 10-3 | Милли | м |
| 109 | Гига | Г | 10-6 | Микро | мк |
| 106 | Мега | М | 10-9 | Нано | н |
| 103 | Кило | к | 10-12 | Пико | п |
| 102 | Гекто | г | 10-15 | Фемто | ф |
| Дека | да | 10-18 | Атто | а |
Международные эталоны хранятся в Международном бюро мер и весов (Франция). Они не подлежат использованию для измерений или калибровки и периодически проверяются путем выполнения абсолютных измерений в соответствующих фундаментальных единицах. Что из себя представляют эти эталоны? Так, эталон метра менялся несколько раз. Первоначально он был определен как десятимиллионная часть меридиана земли, проходящего через Париж, и был выполнен в виде платино- иридиевого стержня. Сегодня метр представляет длину, которую пробегает свет в вакууме за время 1/299792458 с (из этого понятия видно, что по международным стандартам скорость света 299 792 458 м/с). В качестве международной секунды в 1967 г. на XIII Генеральной конференции по мерам и весам определили продолжительность 9 192 631 770 периодов излучения, соответствующих переходу между двумя определенными уровнями основного состояния атома 133Cs.
Измерения проводят с помощью средств измерений.
Средство измерений – техническое устройство, предназначенное для измерений.
Средство измерений, предназначенное для выработки сигнала по измеренным значениям в форме, доступной для непосредственного восприятия наблюдателем, называют измерительным прибором. Результат измерения отображается на индикаторе: стрелочном, цифровом и др.
Все измерения разделяются на прямые и косвенные.
При проведении прямых измерений непосредственно регистрируется численное значение интересующей нас величины Yк. Например, механические стрелочные весы выполняют прямое измерение веса объекта контроля. Под весом объекта прогибается пружина, связанная со стрелкой. Положение стрелки на проградуированном циферблате сразу показывает вес.
При косвенных измерениях интересующая нас величина недоступна прямому измерению. В этом случае наблюдается и измеряется другая величина Zк, которая является некоторой функцией от интересующей нас величины Yк. Например, детектор «Карат», предназначенный для определения пробы золота, первоначально измеряет напряжение, величина которого зависит от электропроводности диагностируемого сплава. Существует определенная зависимость между электропроводностью, значением измеренного напряжения и содержанием золота в сплаве. Соответствующая функциональная связь заложена в электронную память детектора. Результат измерения анализируется с учетом этой функциональной связи и на индикатор выводится номер пробы.
Оценка объема древесины в некотором штабеле досок также осуществляется по косвенным измерениям. Его обычно определяют, измерив линейные размеры штабеля (высоту, ширину, длину). Для определения объема перемножают полученные при измерениях значения.
Любому измерению присущи ошибки, как бы тщательно ни был изготовлен измерительный прибор и выполнены все этапы измерения. Опасность ошибок состоит в том, что они влияют на качество решений, которое принимает человек на основе полученных результатов измерений.
При таможенном контроле зачастую очень важно оценить и указать точность результата измерения. Если ее не учитывать, то можно принять неправильное классификационное решение, в результате которого владелец товара и/или таможня понесет значительные финансовые потери. Пусть химический состав сплава измерен как 32,7% хрома, 33,8% железа и 33,5% никеля. В какую позицию ТН ВЭД его следует отнести? Если погрешность данного измерения составляет ±0,1%, то можно отнести этот сплав к позиции 7202 «Ферросплавы» (так как железа в нем однозначно больше, чем других химических элементов), а если ±1%, то из приведенных результатов нельзя сделать каких либо выводов (нельзя однозначно отнести его к ферросплавам или к сплавам никеля).
Точность, которой следует добиваться при измерении, зависит от его цели. Вовсе не всегда следует стремиться провести измерение как можно более точно, тем более, что проведение особо точных измерений, как правило, требует повышенных материальных и временных затрат. Предположим, что образец сплава содержит в соответствии с анализом 4,95% платины, а точность измерений была ±0,05 %. Ясно, что в данном случае такая точность избыточна, так как сплав даже с гораздо меньшим содержанием платины (более 2%) будет отнесен к позиции 7110 «Платина необработанная или полуобработанная, или в виде порошка».
Изучением различных видов ошибок и причин их возникновения, разработкой методов уменьшения ошибок и их влияния на конечный результат деятельности человека занимаются теория измерений и теория ошибок.
Одна из классификаций ошибок, используемая в теории измерений, показана на рис 3.1.
Личные ошибкисвязаны с действиями человека, проводящего измерения. Он может иметь нарушенное обоняние, цветоощущение, пониженный уровень слуха. Каждый по-своему оценивает положение даже стрелки весов или часов. Личные ошибки зависят от уровня знаний и практической подготовленности, степени утомляемости, ответственности за выполняемую работу и т.п.
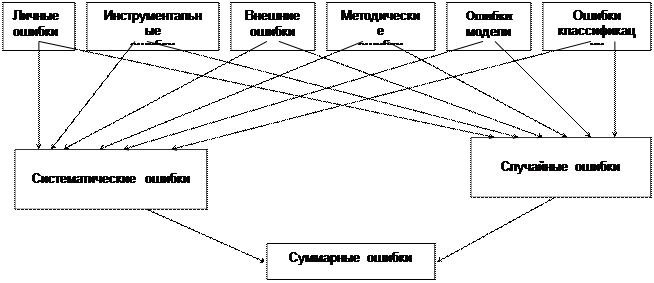
Рис. 3.1. Основные виды ошибок
Инструментальные ошибки возникают вследствие невозможности изготовить измерительное устройство идеально точно. Даже нанесение шкалы на линейку или циферблат измерителя невозможно выполнить с абсолютно одинаковым шагом, не говоря уже о неидеальности изготовления механических частей измерительных механизмов. У электронных измерительных устройств, реализующих цифровые алгоритмы обработки, возможны ошибки округления при оцифровке аналогового сигнала или при вычислениях.
Внешние ошибки связаны с воздействием окружающей среды на измерительное устройство и процесс измерения. Такими воздействиями могут быть колебания напряжения в сети, механические толчки и вибрации, изменения температуры, влажности и давления воздуха, электрические разряды искусственного или естественного происхождения и т.п.
Методические ошибки и ошибки модели связаны с реализуемым в приборе методом измерений.
Ошибки классификации возникают, когда решение принимается путем сравнения измеренного значения с некоторыми априори заданными значениями, описывающими эталонные объекты, к одному из которых надо отнести контролируемый объект.
По своему характеру любая из перечисленных выше ошибок может быть случайной или систематической. Случайными являются ошибки, которые невозможно учесть и воспроизвести при повторных измерениях. Систематические ошибки зачастую обусловлены не учетом важной, существенной связи, присущей наблюдаемому объекту или процессу измерений.
Обычно резкой границы между различными видами ошибок не существует. Одна и та же ошибка может считаться в одних случаях систематической, а в других – случайной. Это, например, может быть связано с длительностью мешающего внешнего воздействия. Если мешающий фактор одинаково действует при всех измерениях, то его можно рассматривать в качестве систематической ошибки.
Все вышерассмотренные виды ошибок могут приводить к неправильным результатам измерения.
Качество измерений, отражающее отклонение результата измерений от истинного значения измеряемой величины, называют погрешностью системы измерения. Фактически погрешность измерения – это число, указывающее возможные границы неопределенности полученного при измерении значения. Ее величина зависит от характеристик самого измерительного прибора, используемого метода измерений, влияния внешних условий на процесс измерений и др.
В теории измерений различают несколько десятков видов погрешностей.
При создании новых измерительных приборов очень важно выделить инструментальные и методические погрешности.
Инструментальными (аппаратными) называют погрешности, которые определяются конструкцией и схемой самого измерительного прибора. Они могут быть определены при его испытаниях и занесены в его паспорт.
Методическими называют погрешности, которые связаны с методом проведения измерений. Примером такой погрешности может служить погрешность измерения напряжения стрелочным вольтметром. При подключении вольтметра его сопротивление шунтирует измеряемую цепь. Поэтому погрешность показания вольтметра зависит от сопротивления измеряемой цепи, так как часть тока, проходящая по катушке вольтметра, определяется не только величиной сопротивления катушки (которое постоянно), но и сопротивлением измеряемой цепи. Чтобы уменьшить погрешность измерения стрелочным вольтметром, его катушку делают с максимально большим сопротивлением. Тогда колебания тока в катушке вольтметра из-за изменения сопротивления измеряемой цепи будут меньше влиять на результат измерения.
В эксплуатационной документации обычно дается 1-2 вида погрешностей, характеризующих качество измерений данным прибором (обычно это некоторые интегральные погрешности).
Погрешности прибора определяют в ходе его поверки, при этом используют образцовые средства измерений с очень низкими погрешностями.
Чаще всего в эксплуатационной документации на измерительный прибор указывают относительную или приведенную погрешности либо их варианты.
Абсолютная погрешность DА = Ап – Ад выражается в единицах измеряемой величины и показывает отклонение результата измерения от действительной величины (Ап – показание прибора, Ад – истинное значение измеряемой величины).
Относительная погрешность – вычисляется (в процентах) как отношение абсолютной погрешности к истинному значению измеряемой величины: d = (DА/Ад) 100%.
Погрешность может меняться при изменении действительного значения измеряемой величины. В таких случаях для прибора указывают приведенную погрешность.
Приведенная погрешность – отношение (в процентах) абсолютной погрешности к значению Ав верхнего предела измерений: dп = (DА / Ав) 100% .
Погрешности, возникающие в нормальных условиях работы измерительного прибора, называют основными. Изменение основной погрешности, обусловленное изменением внешних условий относительно нормальных, вызывает появление дополнительных погрешностей.
При нормировании погрешностей прибора устанавливают пределы допускаемых погрешностей (основной и всех дополнительных), а также нормальные условия и допускаемые отклонения от нормальных значений для всех влияющих факторов. Обобщенной характеристикой пределов допускаемых погрешностей является класс точности измерительного прибора.
Наибольшее значение приведенной погрешности, соответствующее максимально возможной ∆Аmax абсолютной погрешности, допускаемой данным прибором, называется классом точности:
К = (∆Аmax / Аm)∙100%, где
Аm наибольшее значение, которое можно измерить по шкале прибора.
По ГОСТ 1845-52, электроизмерительные приборы делятся на семь классов точности : 0,1; 0,2; 0,5; 1,0; 1.8; 2,5; 4,0.
Значение класса точности помещается на лицевой стороне прибора. Зная К, можно найти наибольшую абсолютную погрешность: ∆Аmax=(К∙Аm)/100.
Все погрешности можно разделить на два типа—систематические и случайные.
Систематические обычно остаются постоянными на протяжении всей серии измерений. Случайные же хаотически изменяются и в равной степени могут быть как положительными (увеличивают значение измеряемой величины по отношению к ее истинному значению), так и отрицательными (уменьшают значение измеряемой величины).
Разновидность случайных ошибок— грубые ошибки или промахи. Их источник - неправильные отсчеты по прибору, неправильная запись отсчета и т.п. В большинстве случаев промахи хорошо заметны, так как соответствующие им отсчеты резко отличаются от других. При обработке результатов измерений такие отсчеты следует отбрасывать. Однако промах можно заметить только, если проделано несколько измерений одной и той же величины. Поэтому, если есть основания полагать, что на результат измерения воздействуют случайные факторы, то нельзя ограничиваться одним измерением, обязательно следует провести их несколько раз. Тогда можно уменьшить погрешность путем статистической обработкой совокупности измерений (обычно определяют среднее значение результата измерения).
Как правило, в методических указаниях в документации к прибору, если его измерения подвержены случайным ошибкам, указывается на необходимость многократных измерений. Например, это относится к прибору «Карат», применяемому для оценки состава сплавов или к приборам дозиметрического контроля.
Предположим, что мы провели серию измерений некоторой физической величины х. Результат отдельного i-го измерения обозначим через хi, а общее число измерений n. Если систематическая ошибка отсутствует, то разумно предположить, что значения измерений расположатся вблизи неизвестного нам истинного значения АДизмеряемой величины, причем отклонения в сторону больших и меньших значений будут равновероятными. Опыт показывает, что во многих случаях такое предположение справедливо. Тогда в качестве наилучшего приближения к истинному значению обычно берут среднее арифметическое 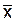 , а возможное отклонение от истинного – как среднеквадратичное Sx отклонение по всем nотдельным измерениям:
, а возможное отклонение от истинного – как среднеквадратичное Sx отклонение по всем nотдельным измерениям:
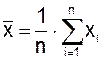 и
и 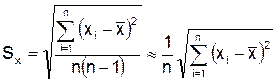 .
.
Систематические ошибки возникают вследствие погрешностей измерительной аппаратуры (спешит или отстает секундомер, сбилась настройка электронного прибора, сместился регулировочный грузик в механических весах и т.д.), а также из-за того, что условия измерения отличаются от нормальных для работы прибора, а поправку на это несоответствие не делают. Например, при определении плотности вещества по объему тела надо учитывать, что размеры тел при повышении температуры обычно увеличиваются, а масса остается одной и той же. Поэтому плотность нагретых тел ниже, чем холодных.
Возможно роль случайных факторов незначительна. Тогда измерение каждой величины проводится, как правило, только один раз, и точность его определяется погрешностью используемого прибора (ее называют приборной).
При оценке результата измерений интервал, в пределах которого с определенной вероятностью может оказаться истинное значение измеряемой величины, часто указывают в виде выражения Ап±ΔА. Величина ΔА называется погрешностью илиошибкойизмерения, а интервал значений от(Ап-ΔА)до (Ап+ΔА)—доверительныминтервалом.
Доверительный интервал не является исчерпывающей характеристикой точности измерения. Нужна количественная характеристика его достоверности, показывающая, насколько можно быть уверенным в том, что истинное значение измеряемой величины окажется в пределах доверительного интервала. Такая характеристика—вероятность того, что значение Апотличается от истинного не более, чем на ΔА —называется доверительной вероятностью.
Пусть результат серии измерений записан в виде Х=25±2 и приведенный доверительный интервал (от 23 до 27) соответствует доверительной вероятности α=0,95. Что это означает?
Пусть измерения производятся большое число раз. Например, сделаем n=100 однотипных измерений. Результаты будут отличаться друг от друга. При указанной доверительной вероятности примерно в 95 случаях результаты будут отличаться от истинного значения измеряемой величины не более чем на Δx=2, а результаты остальных измерений выйдут за пределы доверительного интервала.
Погрешность может описываться достаточно сложной формулой. Так, для дозиметра РМ 1621 основная относительная погрешность измерения мощности эквивалентной дозы описывается выражением d = ±(15+0,0015/Н +0,01Н)%, где Н – измеренная мощность
Оценка погрешностей при косвенных измерениях имеет некоторую особенность. При косвенных измерениях искомая физическая величина А является функцией величин Х, Y, Z, ...., которые были получены с помощью прямых измерений. Результат косвенного измерения записывается в виде:
А ± ΔА,
где A = ƒ(X, Y, Z,…) - значение искомой величины, рассчитанное по средним значениям параметров X, Y, Z, ..., если каждый из них измерялся по нескольку раз; ΔА - абсолютная погрешность косвенного измерения, зависящая от погрешностей измерения параметров X, Y, Z, ... ( т.е. от ΔХ, ΔY, ΔZ, ...).
В простейших случаях абсолютную и относительную погрешность косвенных измерений нетрудно подсчитать. Рассмотрим несколько примеров.
Пусть А = Х+Y. Если известны погрешности ΔX и ΔY , то
А ± ΔА = (X±ΔX) + (Y±ΔY).
Максимальное значение погрешности равно при этом ΔА = ΔX + ΔY.
Такой же будет максимальная абсолютная погрешность, если А=X–Y.
Отсюда следует, что относительные погрешности величин, являющихся суммой или разностью двух параметров, равны соответственно:
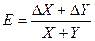 и
и 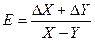 .
.
При косвенных измерениях контролируемый параметр может являться некоторой функцией от нескольких измерений. В таких случаях при определении возможных погрешностей надо учитывать вид функции. Например, площадь (А) обычно определяется путем перемножения результатов измерений линейных размеров длины (X) и ширины (Y) объекта, т.е. A= X.Y.
Тогда
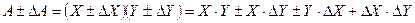
Обычно, последнее слагаемое ΔX.ΔY этой формулы значительно меньше остальных и им можно пренебречь. Тогда абсолютная погрешность:
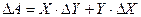 , а относительная
, а относительная

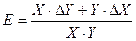 или
или 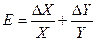 .
.
Дата добавления: 2018-09-24; просмотров: 762;
