Тема 12. Излучение эмв

Сущность процесса излучения. Возможность излучения как следствие уравнений Максвелла. Элементарный электрический излучатель. Анализ структуры поля. Особенности ЭМП в ближней зоне. Поле излучателя в дальней зоне: ориентация векторов ЭМП, фронт ЭМВ. ДН элементарного электрического излучателя. Излучаемая мощность и сопротивление излучения.

Элементарный магнитный излучатель. Структура поля излучателя и его характеристики. Элементарная рамочная антенна как физический аналог элементарного магнитного излучателя.

Элемент Гюйгенса. Структура поля элемента Гюйгенса.

Указания к теме

Необходимо обратить внимание на то, что законы излучения ЭМП и распространения энергии в виде ЭМВ следуют из системы уравнений Максвелла, изучить ДН и основные параметры элементарных излучателей.

Следует обратить внимание на применение принципа двойственности и понятия «магнитный ток» для упрощения расчетов ЭМП некоторых излучателей. Необходимо научиться разделять пространство около излучателя на зоны, знать особенности каждой зоны, необходимо запомнить особенности поведения ЭМП излучателей в дальней зоне.

Основные сведения

Из системы уравнений Максвелла вытекает вывод о волновом характере ЭМП. Если в некоторой области пространства происходит изменение тока, это возмущение не ограничивается данной областью, а образует ЭМВ, которая отрывается от источника ЭМП и распространяется в свободном пространстве.

Явление излучения ЭМВ проявляется в различных областях электротехники и радиотехники. В одних случаях излучение желательно (антенны), в других оно оказывается вредным (линия передачи информации).

ЭМП системы токов, которые изменяются во времени по гармоническому закону и заключены внутри объема V, ограниченного замкнутой поверхностью S (рис. 12.1), удобно выразить через . Начало координат располагают в области V, которая вписывается в сферу радиуса r_0max = d_max/2 (d_max – максимальный линейный размер антенны).

Проинтегрировав уравнение (11.11) для комплексных амплитуд по области V, получаем

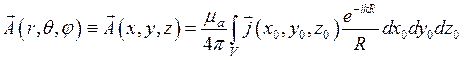, (12.1)

где – расстояние до точки наблюдения М(х, y, z) от произвольной точки антенны (области V) М₀(х₀, y₀, z₀); 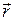– радиус вектор точки М, 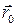– радиус вектор точки М₀; 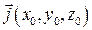– функция распределения тока в области V; 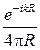– скалярная функция Грина с аргументом R, выражающая сферическую волну, расходящуюся от точечного источника.

Из формулы (12.1) следует, что 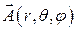ЭМП произвольной антенны представляет суперпозицию сферических волн (e^–ikR/R), излучаемых каждым элементом антенны с функцией распределения тока .

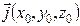Для удобства анализа излучающих систем пространство около антенны целесообразно разделить на такие зоны: ближнюю, промежуточную и дальнюю.

Структура ЭМП антенны в дальней зоне.Для радиосвязи обычно представляет интерес ЭМП на большом расстоянии от антенны

r_0max=max( )<< r = ( ) . (12.2)

С учетом (12.2) выражение (12.1) примет вид

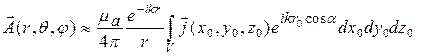. (12.3)

Область пространства, где ЭМП антенны описывается выражением (12.3), называется дальней зоной антенны. В данном приближении разность фаз ЭМВ, излучаемых различными точками антенны, не зависит от их расстояния до точки наблюдения. Хотя ЭМВ в дальней зоне имеет вид элементарной сферической волны, в точке наблюдения она может считаться плоской. Это значит, что в точке наблюдения М(х, y, z) в рассматриваемой области пространства ЭМП от различных излучающих элементов системы складываются уже как плоские, а не сферические ЭМВ. Величина 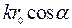определяет фазовый сдвиг плоской волны, приходящей в точку наблюдения от элемента антенны в точке 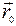относительно аналогичного элемента, расположенного в начале координат.

Используя приближение (12.3) и вычисляя компоненты поля по формулам (11.4) с учетом членов, пропорциональных 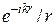, получим

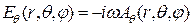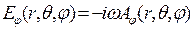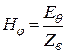, , , . (12.4)

Как видно из формул (12.4), в дальней зоне поперечные по отношению к радиальному направлению компоненты напряженностей ЭМП полностью определяются соответствующими составляющими , а ЭМВ в дальней зоне в общем случае имеет эллиптическую поляризацию.

Радиальные составляющие ЭМП 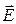и 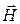убывают быстрее 1/r², и ими в приближении дальней зоны можно пренебречь. ЭМП в дальней зоне имеет чисто поперечный характер, а у вектора останется только радиальная составляющая ( 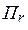) [1].

Примерное расстояние от антенны до области дальней зоны R_ДЗ оценивают, задав допустимую ошибку фазы p/8 (22,5º) в (12.3), что дает

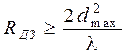. (12.5)

Формула (12.5) для расстояния дальней зоны носит оценочный характер, но даже для этой цели она применима не всегда.

Дело в том, что при переходе от уравнения (12.1) к (12.3) упрощалось подынтегральное выражение без учета функции распределения тока. Более точные исследования [35, 36] показывают, что формулу (12.5) можно использовать лишь тогда, когда амплитуда и фаза распределения тока меняются медленно на расстояниях порядка l. В противном случае расстояние дальней зоны значительно увеличивается.

Угловые распределения ЭМП в дальней зоне не зависят от расстояния. Как наиболее общую характеристику направленности излучающей системы используют величину 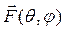, которая называется нормированной диаграммой направленности (ДН) по полю для соответствующих компонент: F_Q (Q, j) по углу места, F_j (Q, j) по азимуту.

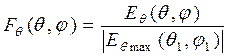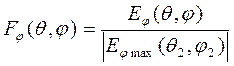; , (12.6)

где Q₁, j₁ и Q₂, j₂ – направления максимума излучения для F_Q и F_j [1].

Характеристика 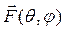представляет собой векторную комплексную ДН антенны[1, 32, 34], ее удобнее записать в виде

, (12.7)

где 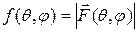– амплитудная ДН (ее квадрат – ДН антенны по мощности); 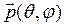– нормированная векторная функция ( 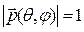), характеризующая зависимость поляризации излучения от направления (поляризационная ДН); 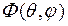– аналогичная зависимость фазы ЭМП (фазовая ДН) [1, 32].

На расстояниях меньших RДЗ, которое определяется формулой (12.5), дальняя зона излучающей системы плавно переходит в промежуточную зону, иногда называемую областью дифракции Френеля [1, 32]. ЭМП в промежуточной и ближней зонах имеет по сравнению с дальней зоной сложный характер.