Экспоненциальные модели и модели с насыщением

В отличие от использования полиномиальных кривых использование экспоненциальных моделей предполагает, что дальнейшее развитие процесса находится в зависимости от уровня, достигнутого на данный момент времени, например, прирост зависит от значения функции. Экспоненциальные модели хорошо описывают процессы, носящие лавинообразный характер. Существует множество моделей экспоненциальных кривых роста, но на практике применяются лишь некоторые из них.

Некоторые экспоненциальные модели роста характеризуются наличием горизонтальных асимптот, т.е. являются моделями с насыщением. Возрастающие модели с насыщением стремятся к асимптоте снизу. Это делает возможным их применение для прогнозирования тех процессов, которые не могут возрастать бесконечно (например, объём продаж). Убывающие модели с насыщением стремятся к асимптоте сверху. Часто асимптотой выступает нулевое значение. В таком случае математическая модель имеет конкретный экономический смысл: натуральные показатели промышленного производства при их снижении не могут опускаться ниже нуля, но могут неограниченно к нему стремиться.

Отдельные экспоненциальные модели характеризуются наличием вертикальных асимптот, т.е. ограничением величины t при определённых условиях. Это накладывает существенное ограничение на их использование: математическая модель должна быть положительно определена не только в течение периода моделирования исходных данных, но также и на всей длине периода упреждения прогноза.

1. Простая экспонента:

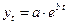(4.11)

определена на всей числовой оси. Обязательным условием данной функции является a > 0, но на величину b ограничения не накладываются. Если b < 0, то функция является убывающей с замедлением и стремится к нулю. Если b > 0, то функция возрастает с ускорением на всей длине числовой оси.

2. Показательная функция:

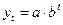(4.12)

также определена на всей числовой оси. Обязательным условием данной функции является a > 0 и b > 0. Если b < 1, то функция является убывающей и стремится от горизонтальной асимптоты k_y = a к нулю. Если b > 1, то функция возрастает на всей длине числовой оси, начиная с асимптоты k_y = a.

В некоторых случаях показательную функцию записывают в виде:

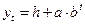(4.13)

и называют модифицированной экспонентой. В данном случае ветви модифицированной экспоненты смещаются вертикально на величину h, которая является горизонтальной асимптотой функции.

3. Степенная функция:

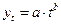(4.14)

определена на всей длине числовой оси. Обязательным условием является a > 0. Степенная функция может быть трёх видов в зависимости от величины b. Если b < 0, то функция является убывающей с замедлением и стремится от горизонтальной асимптоты k_y = a к нулю. Если b < 1, то функция является медленно возрастающей на всей длине числовой оси, начиная с асимптоты k_y = a. Если b > 1, то функция является быстро возрастающей на всей длине числовой оси, начиная с асимптоты k_y = a.

4. К следующему классу экспоненциальных моделей относятся модели гиперболы. Основной особенностью данных моделей является наличие вертикальных асимптот. Гипербола I типа имеет вид:

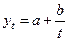(4.15).

Обязательным условием является a > 0. Если b < 0, то функция является возрастающей с замедлением, но имеет вертикальную асимптоту 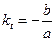, к которой стремится справа. В том случае, если k_t > 1, то использовать данную функцию для аппроксимации исследуемого временного ряда нельзя, т.к. моделировать начальные значения невозможно. Функция также имеет горизонтальную асимптоту k_y = a, к которой стремится снизу. Если b > 0, то функция убывает с замедлением на всей длине числовой оси без вертикальных асимптот, но с горизонтальной асимптотой k_y = a.

5. Гипербола II типа:

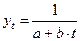(4.16)

определена только для a > 0. Если b < 0, то функция является возрастающей с ускорением, но имеет вертикальную асимптоту 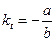, к которой стремится слева. В том случае, если k_t < (n + L), где L – период упреждения прогноза, то использовать данную функцию для аппроксимации исследуемого временного ряда нельзя, т.к. моделировать прогнозные значения невозможно. Если b > 0, то функция убывает с замедлением на всей числовой оси без вертикальных асимптот, но с горизонтальной асимптотой k_y = 0.

6. Гипербола III типа (простая рациональная функция):

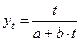(4.17)

определена только для a > 0. Если b < 0, то функция аналогична гиперболе II типа, но с большим ускорением. Если b > 0, то функция возрастает с замедлением на всей длине числовой оси без вертикальных асимптот, но с горизонтальной асимптотой 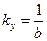, к которой стремится снизу.

7. Следующей функцией является простая логарифмическая функция, которая имеет вид:

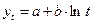(4.18).

Обязательным условием является a > 0. Если b < 0, то функция является убывающей с замедлением и имеет вертикальную асимптоту 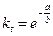, к которой стремится слева. В том случае, если k_t < (n + L), то использовать данную функцию для аппроксимации исследуемого временного ряда нельзя. Если b > 0, то функция возрастает с замедлением на всей длине числовой оси без вертикальных асимптот.

В экономике часто встречаются процессы, которые сначала растут медленно, затем ускоряются, а затем снова замедляют свой рост, стремясь к какому-либо пределу. В качестве примера можно привести процесс изменения спроса на новые продукты, который способен достигать некоторого уровня насыщения. Для моделирования подобных процессов используются S-образные кривые.

8. Обратнологарифмическая функция имеет вид:

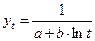(4.19).

Обязательным условием является a > 0. Если b < 0, то функция является возрастающей S-образной кривой: на первом этапе рост кривой происходит с замедлением, затем – с постоянной скоростью, в конце – с ускорением. Функция имеет вертикальную асимптоту 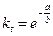, к которой стремится слева, аналогичную асимптоте простой логарифмической функции. Если b > 0, то функция убывает с замедлением на всей длине числовой оси без вертикальных асимптот.

9. S-образная функция имеет вид:

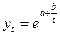(4.20).

Обязательным условием является a > 0. Если b < 0, то наблюдаются два вида данной функции в зависимости от величины a. Если a < -b, то функция имеет вид возрастающей S-образной кривой: на первом этапе происходит рост функции с ускорением, на последнем – с замедлением. Если a > -b, то функция является возрастающей с замедлением. В любом случае S-образная функция имеет горизонтальную асимптоту 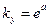, к которой стремится снизу. Если b > 0, то функция убывает с замедлением на всей длине числовой оси с горизонтальной асимптотой 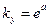, к которой стремится сверху.

10. Кривая Гомперца имеет аналитическое выражение:

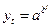(4.21),

где a и b – положительные величины. В зависимости от величины коэффициента a кривая Гомперца может быть двух видов.

Если a < 1, то кривая Гомперца является S-образной кривой. Тогда в ней выделяются четыре участка: на первом – прирост функции незначителен, на втором – прирост увеличивается, на третьем – прирост постоянен, на четвёртом – происходит замедление темпов прироста, и функция неограниченно приближается к горизонтальной асимптоте.

Если b < 1, то функция является возрастающей и стремится снизу к горизонтальной асимптоте. Тогда, если t ® ∞, то b^t ® 0, а значение функции y_t ® 1. Можно утверждать, что k_y = 1. Поэтому иногда кривую Гомперца записывают в следующем виде:

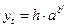(4.22),

что позволяет утверждать горизонтальную асимптоту k_y = h, со значением много большим единицы.

Если b > 1, то функция является убывающей S-образной кривой и стремится сверху к нулю. Таким образом, значения функции могут лежать в интервале (0;1). При использовании соотношения (6.18) можно добиться области значений функции Гомперца (0;h).

Если a > 1, то кривая Гомперца является экспоненциальной кривой. Если b < 1, то функция является убывающей и стремится сверху к горизонтальной асимптоте k_y = 1 или k_y = h в зависимости от модификации функции (4.21) или (4.22) соответственно.

Если b > 1, то функция является неограниченно возрастающей. Такое соотношение коэффициентов кривой Гомперца почти не используется, т.к. аналогичных её поведению процессов в социально-экономической жизни общества практически не существует.

11. Логистическая кривая I типа имеет вид:

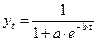(4.23).

Обязательным условием является a > 0. Если b < 0, то функция является убывающей S-образной кривой, стремящейся сверху к нулю. Если b > 0, то функция возрастает на всей длине числовой оси и стремится снизу к горизонтальной асимптоте k_y = 1. Таким образом, значения функции лежат в интервале (0;1). Если записать логистическую кривую I типа в виде:

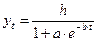(4.24),

можно добиться области её значений (0;h), что позволяет применять функцию для аппроксимации динамики социально-экономических процессов.

12. Логистическая кривая II типа (кривая Перла-Рида) имеет вид:

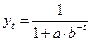(4.25).

Обязательным условием данной функции является a > 0 и b > 0. Если b < 1, то функция является убывающей S-образной кривой, стремящейся сверху к нулю. Если b > 1, то функция возрастает на всей длине числовой оси и стремится снизу к горизонтальной асимптоте k_y = 1. Таким образом, значения функции лежат в интервале (0;1). Если записать логистическую кривую II типа в виде:

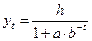(4.26),

можно добиться области её значений (0;h).

Конфигурация логистической кривой близка конфигурации кривой Гомперца, но логистическая кривая имеет точку симметрии, которая совпадает с точкой перегиба.