ДИАЛЕКТИЧЕСКОЕ ЕДИНСТВО 0-МЕРНОЙ ТОЧКИ

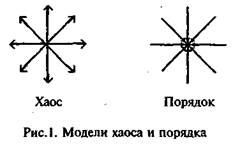
Структура пространства дает нам возможность обсудить истоки полного хаоса и высшей упорядоченности. Они находятся в диалектическом единстве 0-мерной точки. Расходящиеся во все стороны направления олицетворяют полную неупорядоченность (хаос). Сходящиеся в одну точку направления, наоборот, являются воплощением полной упорядоченности.

Однако раздвоением единого на противоположности дело не ограничивается. 0-мерных точек — бесконечное множество, поэтому возможности хаоса неограниченны. Но это же и ведет к возможности образования центров сходящихся направлений, т.е. хаос направлений содержит в себе возможность упорядоченности. То же самое произойдет, если представить, что в каждой из бесконечного множества точек направления расходятся — одновременно будет возникать хаос. Это говорит о том, что структура пространства не допускает ни полного хаоса, ни полного порядка. Но положение «фифти-фифти» (50x50) в природе не наблюдается. Значит, у ПРИРОДЫ есть некий набор средств противостоять нарастанию хаоса и развитие жизни на Земле — яркий тому пример.

Равнозначность точек и направлений говорит о равновесном состоянии пространства и является основой его существования. Любое локальное нарушение этого пространства вызывает реакцию противодействия, которая создает динамическое равновесие с тем, что вызвало это нарушение. Эти проявления называются сегодня полями. Таков один из уровней бытия.

ВЫВОДЫ

Современный уровень развития проблематики порядка и хаоса формулирует три существенных дополнения к традиционным взглядам:

1. Представление о хаосе как источнике гибели и деструкции (разрушения) заменяется более емким пониманием хаоса как основания для установления упорядоченности, причины спонтанного структурирования.

2. Определение хаоса как состояния, производного от первичной неустойчивости материальных взаимодействий, подразумевается универсальной характеристикой, охватывающей живую, косную (неживую) и социально-организованную материю.

3. Хаос — это не только бесформенная масса, а сверхсложноорганизованная последовательность, логика которой представляет большой интерес.