Относительными величинами сравнения

Представляет собой соотношение одного и того же абсолютного показателя, характеризующего разные объекты (предприятия, фирмы, регионы).

ОВС = 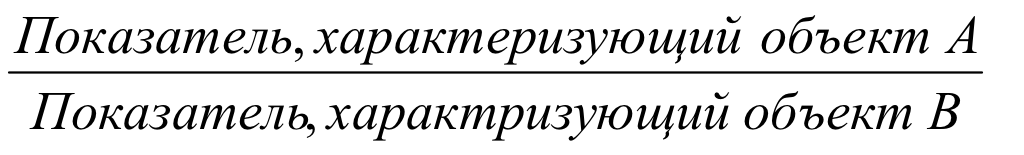(4.11.)

Комплексное использование абсолютных и относительных величин дает всестороннюю характеристику изучаемого явления.

Понятие, назначение и принципы построения средних величин, используемых в статистике сферы услуг

Средней величиной называется обобщающий показатель, характеризующий типичный уровень варьирующего количественного признака на единицу совокупности в определенных усло­виях места и времени.

Объективность и типичность статистической средней обеспечивается лишь при определенных условиях. Первое условие - средняя должна вычисляться для качественно однородной совокупности. Для получения однородной совокупности необходима группировка данных, поэтому расчет средней должен сочетаться с методом группировок. Второе условие - для исчисления средних должны быть использованы массовые данные. В средней величине, исчисленной на основе данных о большом числе единиц (массовых данных), колебания в величине при­знака, вызванные случайными причинами, погашаются и проявляется общее свойство (типичный размер признака) для всей совокупности. Средняя величина размерность, что и признак у отдельных единиц совокупности.

При использовании средних в практической работе и научных исследованиях необходимо иметь в виду, что за средним показателем скрываются особенности различных частей изучаемой совокупности, поэтому общие средние для однородной совокупности должны дополняться групповыми средними, характеризующими части совокупности.

В экономических исследованиях и плановых расчетах применяются две категории средних: степенные средние; структурные средние.

К категории степенных средних относятся: средняя арифметическая, средняя гармоническая, средняя квадратическая, средняя геометрическая. Величины, для которых исчисляется средняя, обозначаются буквой х. Черта вверху символизирует процесс осреднения индивидуальных значений. Частота - повторяемость индивидуальных значений признака - обозначается буквой F.

В зависимости от степени получаются различные виды средних величин, их формулы представлены в таблице 4.1.

Таблица 4.1.

Формулы различных видов степенных средних величин

Значение к	Наименование средней	Формула средней
простая	взвешенная
-1	Гармоническая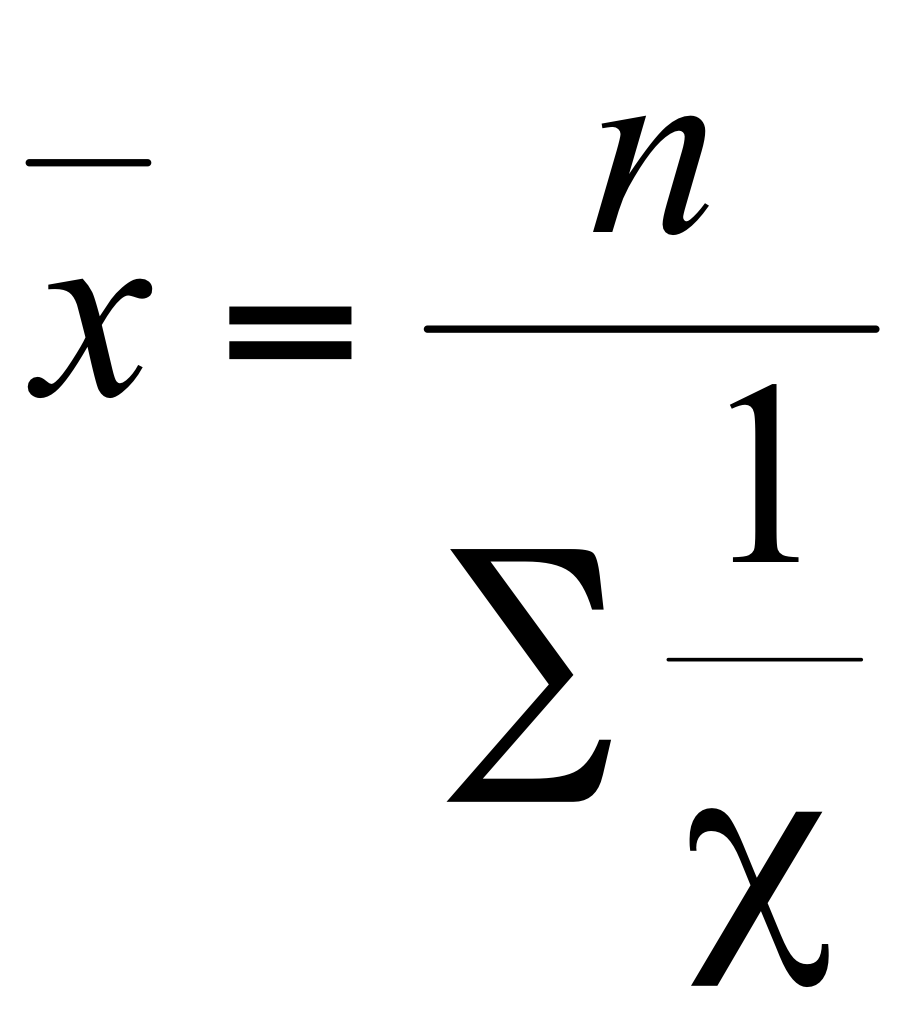
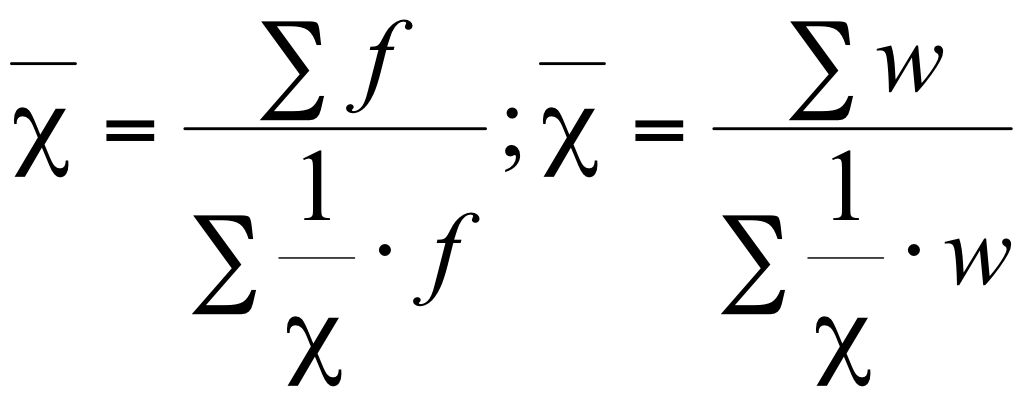
	Геометрическая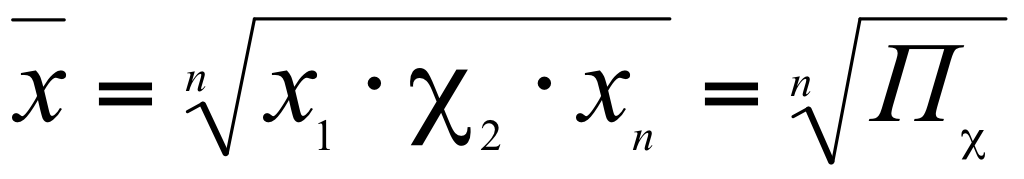
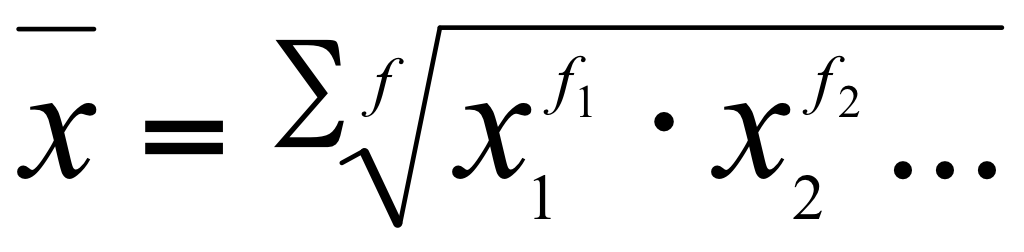
	Арифметическая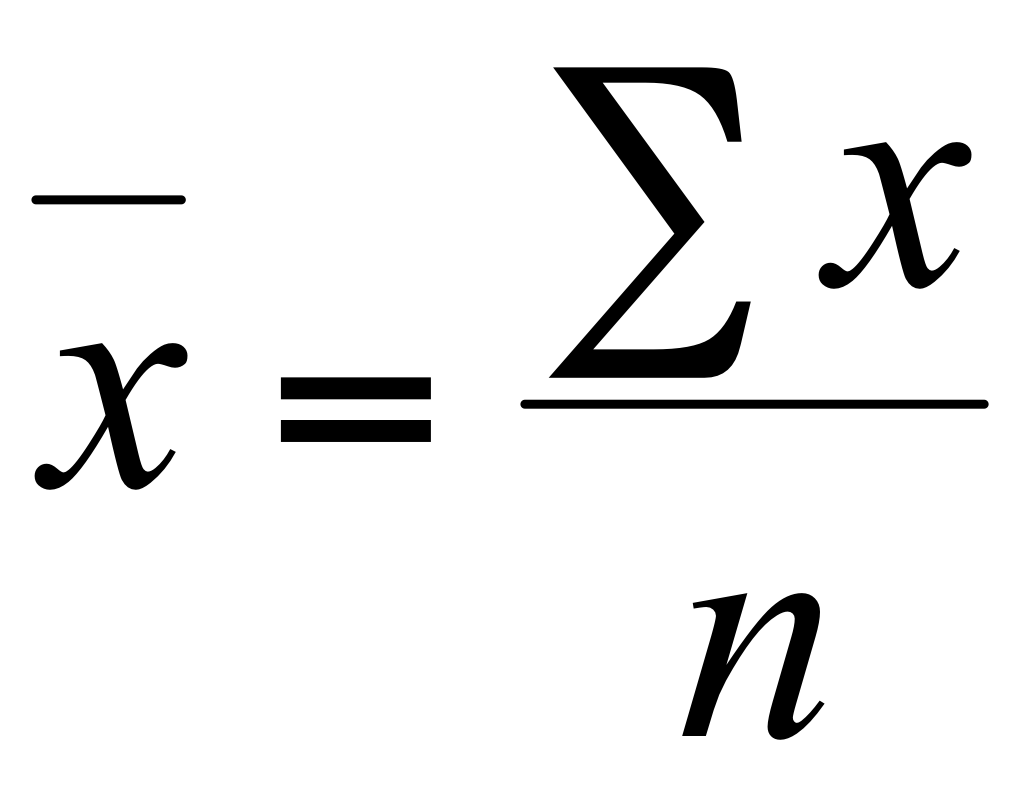
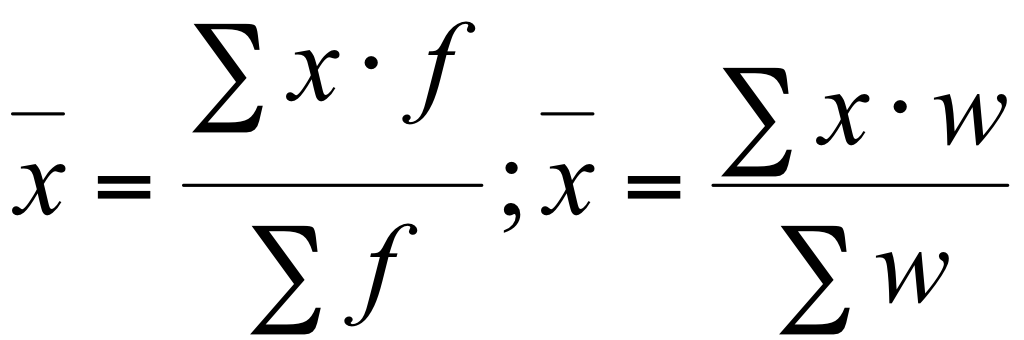
	Квадратическая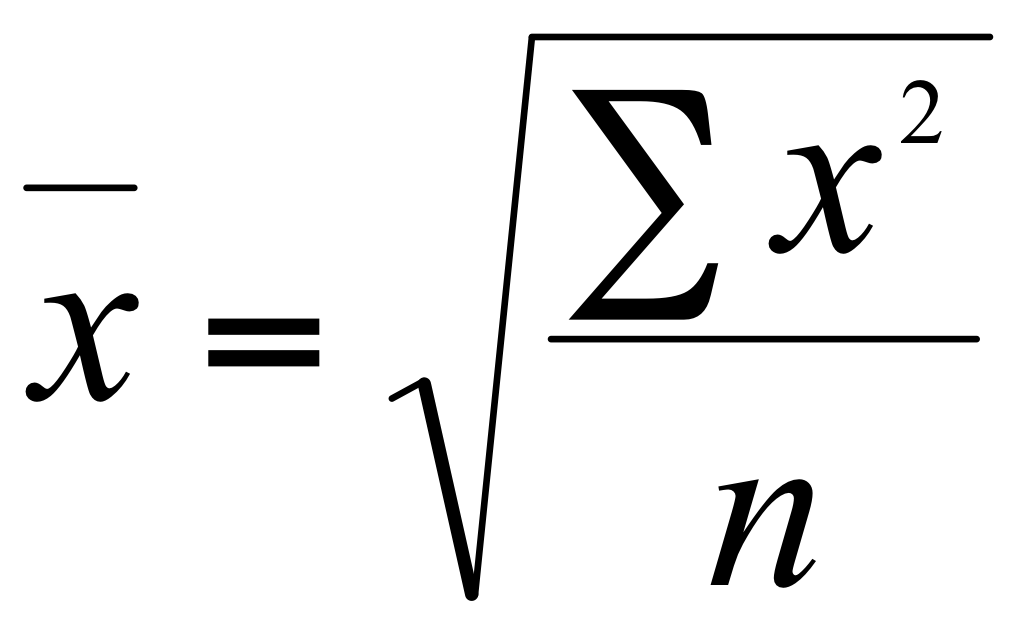

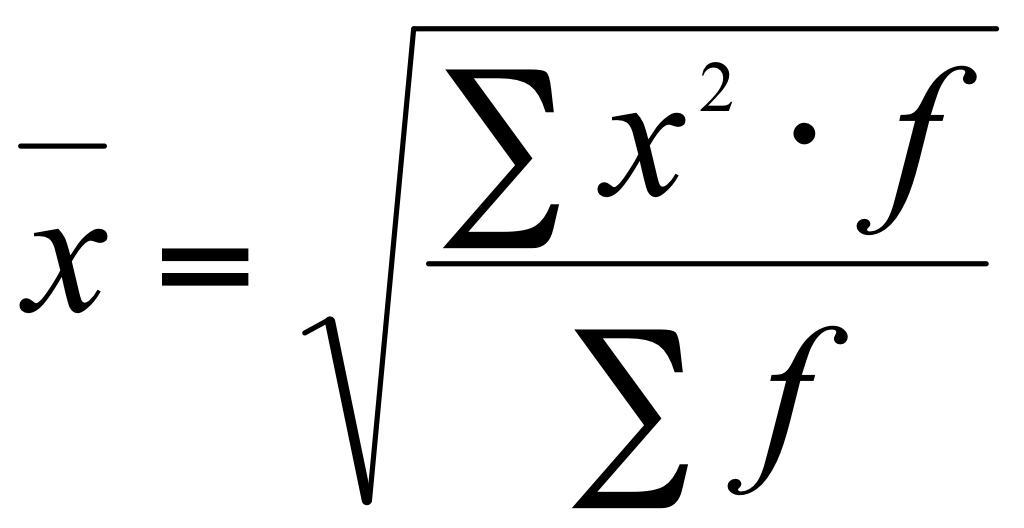
Как видно из таблицы 3.1., взвешенные средние учитывают, что отдельные варианты значений признака имеют различную численность, поэтому каждый вариант «взвешивают» по своей частоте, т. е. умножают на нее. Частоты при этом называются статистическими весами или просто весами средней.

Однако необходимо учитывать, что статистический вес - понятие более широкое, чем частота. В качестве веса могут применяться какие-либо другие величины (в таблице они обозначены буквой w). Например, при расчете средней продолжительности рабочего дня по предприятию единственно правильным будет взвешивание по количеству отработанных человеко-дней. Частоты отдельных вариантов могут быть выражены не только абсолютными величинами, но и относительными - частостями.

Величины степенных средних, рассчитанных на основе одних и тех же индивидуальных значений признака при различных значениях степени (K:), не одинаковы. Чем выше степень K средней, тем больше величина самой средней.

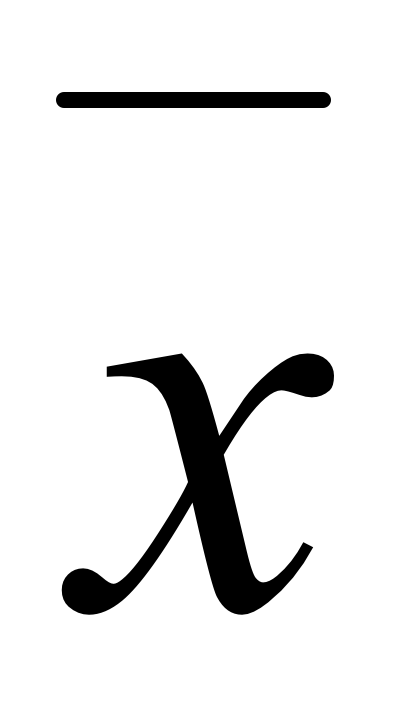гарм < 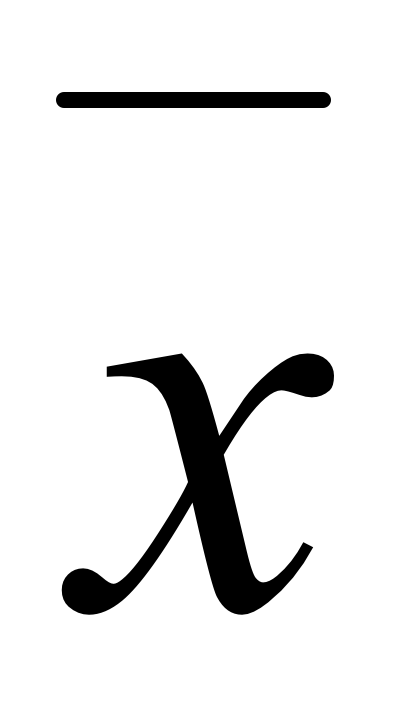геом < 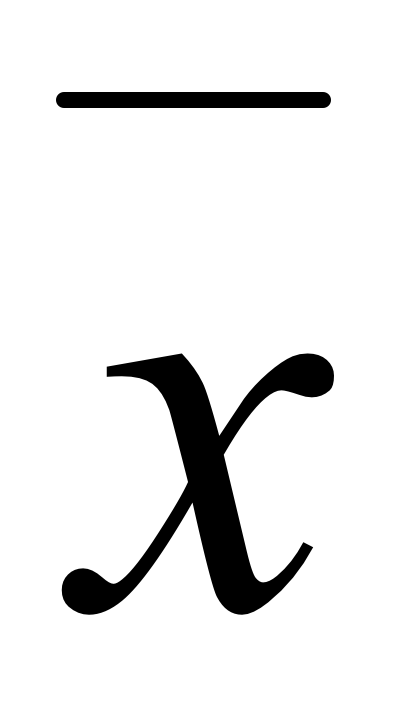арифм < 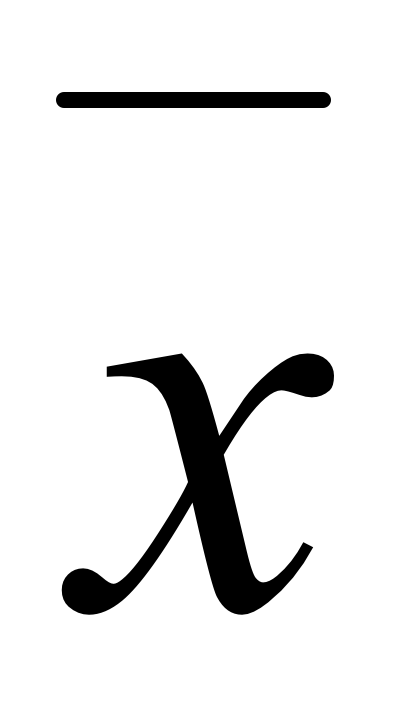квадр (4.12.)

Вопрос о выборе средней решается в каждом отдельном случае, исходя из задачи исследования, материального содержания изучаемого явления и наличия исходной информации. Он состоит из нескольких этапов:

· устанавливается определяющий показатель, т. е. обобщающий показатель совокупности, от которого зависит величина средней;

· определяется математическое выражение для определяющего показателя;

· производится замена индивидуальных значений средними величинами;

· решение уравнения средней.

Основополагающее правило при этом заключается в том, что величины, представляющие собой числитель и знаменатель средней, должны иметь определенный логический смысл.

Средняя арифметическая и средняя гармоническая наиболее распространенные виды средней, получившие широкое применение в плановых расчетах, при расчете общей средней из средних групповых, а также при выявлении взаимосвязи между признаками с помощью группировок. Выбор средней арифметической и средней гармонической определяется характером имеющейся в распоряжении исследователя информации.

Средняя квадратическая применяется для расчета среднего квадратического отклонения (а), являющегося показателем вариации признаков, а также в технике (например, при сооружении трубопроводов).

Средняя геометрическая (простая) используется при вычислении среднего коэффициента роста (темпа) в рядах динамики. Структурные средние - мода и медиана - в отличие от степенных средних, которые в значительной степени являются абстрактной характеристикой совокупности, выступают как конкретные величины, совпадающие с вполне определенными вариантами совокупности. Это делает их незаменимыми при решении ряда практических задач.

Модой называется значение признака, которое наиболее часто встречается в совокупности (в статистическом ряду).

Медианой называется значение признака, которое лежит в середине ранжированного ряда и делит этот ряд на две равные по численности части.

Ранжированный ряд - ряд, расположенный в порядке возрастания или убывания значений признака.

Для определения медианы сначала определяют ее место в ряду, используя формулу

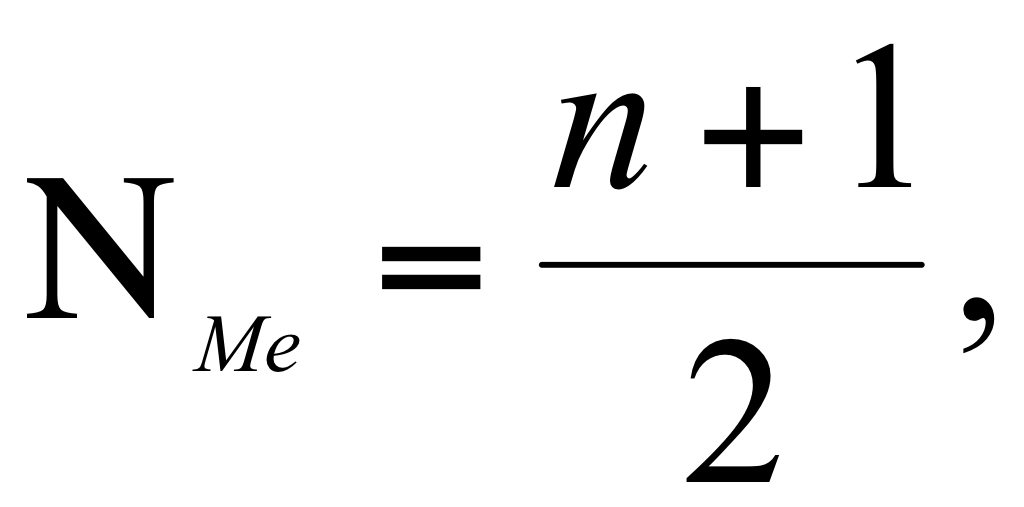(4.13.)

где n – число членов ряда.

Если ряд состоит из четного числа членов, то за медиану условно принимают среднюю арифметическую их двух срединных значений.

Применяется мода при экспертных оценках, при определе­нии наиболее ходовых размеров обуви, одежды, что учитывается при планировании их производства. Медиана используется при статистическом контроле качества продукции и технологического процесса на промышленных предприятиях; при изучении распределения семей по величине дохода и др. Мода и медиана имеют преимущество перед средней арифметической для ряда распределения с открытыми интервалами.