Местные потери напора. Местные гидравлические сопротивления

Местными гидравлическими сопротивлениями называют любые участки гидравлической системы, где имеются резкие изменения размеров поперечного сечения канала, по которому движется жидкость, резкие повороты канала, элементы управляющей и запорной арматуры, установленные для регулирования направления потока и расхода жидкости (рис.9.1 и рис.9.3).

Потери напора на местном сопротивлении определяются по формуле Вейсбаха

,

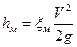(9.1)

где 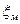-- коэффициент местного сопротивления.

Коэффициент местного сопротивления зависит от геометрической формы и размеров сечения канала в этом элементе гидравлической системы. Теоретическое определения коэффициента 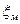в большинстве случаев затруднительно и его определяют по результатам экспериментальных исследований.

Рис. 9.1

Схема экспериментальной установки для определения коэффициента местного сопротивления “внезапное расширение” приведена на рис. 9.2.

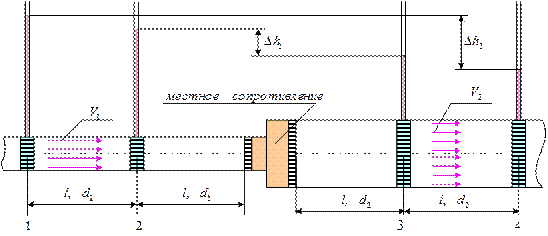Рис. 9.2

Потери напора между сечениями 2 и 3 определяются, как разность показаний пьезометров 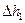, а изменение напора между сечениями 1 и 4 – это разность показаний пьезометров 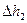. Предполагая 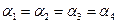, можно записать уравнение Бернулли для сечений 2-3 и сечений 1-4

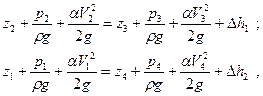
(9.2)

где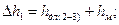

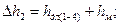
Равенство длин участков и диаметров труб между сечениями 1 и 2, сечением 2 и началом местного сопротивления; окончанием местного сопротивления и сечением 3, сечениями 3 и 4, дает основание сказать – потери по длине на участке 1-4 в два раза больше потерь по длине на участке 2-3

.

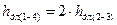(9.3)

При условии, что 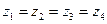, уравнения (9.2) с учетом (9.3) принимают вид

(9.4)

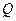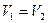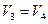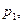
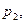
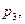
При выполнении исследования, в гидравлической системе, включающей местное сопротивление, устанавливают определенный расход жидкости , что позволяет рассчитать средние скорости потока , . Давления 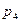определяют по показаниям пьезометров в сечениях 1, 2, 3 и 4. После чего по уравнениям (9.4) легко расчитать потери напора по длине 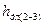и местные потери напора 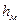. Затем, используя формулу (9.1) легко найти значение коэффициента 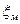, для изучаемого местного сопротивления

.

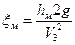(9.3)

Необходимо добавить, что, как правило, значение коэффициента местных потерь 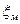определяют по отношению к кинетическому напору в выходном сечении местного сопротивления, но, если в том будет необходимость, коэффициент местных потерь можно пересчитать и на кинетический напор на входе в местное сопротивление (в рассматриваемом примере это ).

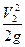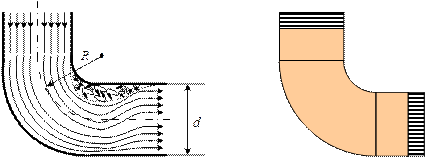Рис. 9.3
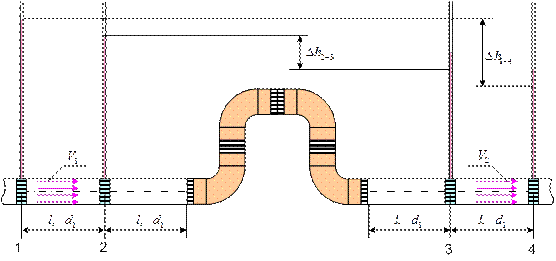Рис. 9.4

В том случае, когда местные сопротивления находятся на расстоянии меньше (25…50)d друг от друга (d – диаметр трубопровода, соединяющего местные сопротивления) можно наблюдать их взаимное влияние. Такие сопротивления нужно рассматривать, как одно сложное сопротивление (рис. 9.4).

Табл. 9.1

Местное сопротивление	Характеристики местного сопротивления
Вентиль открытый	открыт полностью	D, мм
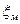
	10,8	6,1	4,6	4,1
Дроссель с плоско скошенным диском	При
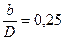
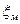
	0,1	0,36	3,05	71,5
	-
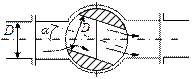
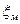
	0,36	2,7	18,2
Задвижка	S/D	D, мм
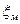
		0,33	0,16	0,14
3/4	0,9	0,68	0,55
1/2	4,1	3,0	2,6
1/4		20,0

Местное сопротивление, создаваемое соединением четырех уголков (рис.9.3), не будет эквивалентно четырем местным сопротивлениям “плавный поворот на 90^о “ ( ).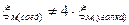

Если расстояния между отдельными местными сопротивлениями достаточно велико для того, чтобы искажение эпюры скоростей, вызванное одним из них, сказывалось на сопротивлении, лежащем ниже по течению, принцип суммирования потерь дает надежные результаты.

В завершении приведем некоторые рекомендации по определению коэффициента местного сопротивления из справочной литературы (табл. 9.1).

Для местного сопротивления “плавный поворот на 90^о “ при 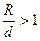коэффициент местного сопротивления рекомендуется определять по формуле

.

(9.4)