Электромагнитные волны
Из уравнений Максвелла вытекает существование электромагнитных волн– переменного электромагнитного поля, распространяющегося в вакууме с конечной скоростью 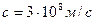 .
.
Можно показать, что для однородной и изотропной среды вдали от зарядов и токов, создающих электромагнитное поле, из уравнений Максвелла следует, что векторы напряжённостей электрического 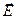 и магнитного
и магнитного 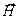 полей удовлетворяют уравнениям:
полей удовлетворяют уравнениям:
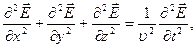 (124)
(124)
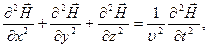 (125)
(125)
где 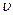 - фазовая скорость.
- фазовая скорость.
Всякая функция, удовлетворяющая уравнениям (124) и (125), описывает некоторую волну. Следовательно, электромагнитные поля действительно могут существовать в виде электромагнитных волн. Фазовая скорость электромагнитных волн определяется выражением
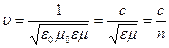 , (126)
, (126)
где 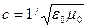 - скорость электромагнитной волны в вакууме,
- скорость электромагнитной волны в вакууме, 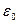 ,
, 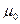 - электрическая и магнитная постоянные,
- электрическая и магнитная постоянные, 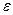 ,
, 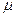 - диэлектрическая и магнитная проницаемости среды,
- диэлектрическая и магнитная проницаемости среды, 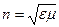 - показатель преломления среды.
- показатель преломления среды.
В вакууме ( 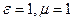 )
) 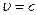 ,
, 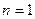 . Поскольку
. Поскольку 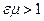 скорость электромагнитной волны в среде всегда меньше, чем в вакууме, т.е.
скорость электромагнитной волны в среде всегда меньше, чем в вакууме, т.е. 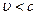 .
.
Длина электромагнитной волны
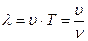 .
.
Следствием теории Максвелла является поперечность электромагнитных волн: векторы 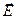 и
и 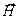 взаимно перпендикулярны и лежат в плоскости, перпендикулярной вектору скорости
взаимно перпендикулярны и лежат в плоскости, перпендикулярной вектору скорости 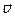 распространения волны, причём векторы
распространения волны, причём векторы 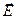 ,
, 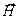 и
и 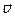 образуют правовинтовую систему (рис. 25). Из уравнений Максвелла следует также, что в электромагнитной волне векторы
образуют правовинтовую систему (рис. 25). Из уравнений Максвелла следует также, что в электромагнитной волне векторы 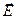 и
и 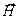 всегда колеблются в одинаковых фазах, причём мгновенные значения напряжённостей электрического и магнитного полей электромагнитной волны в любой точке связаны соотношением:
всегда колеблются в одинаковых фазах, причём мгновенные значения напряжённостей электрического и магнитного полей электромагнитной волны в любой точке связаны соотношением:
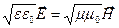 . (127)
. (127)
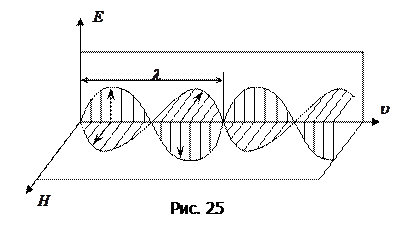 Источником электромагнитных волн может быть любой колебательный контур или проводник, по которому течёт переменный ток. Однако излучающая способность источника определяется его формой, размерами и частотой колебаний. Чтобы излучение играло заметную роль, необходимо увеличить объём пространства, в котором электромагнитное поле создаётся. Поэтому для получения электромагнитных волн непригодны закрытые колебательные контуры (рис. 17), т.к. в них электрическое поле сосредоточено между обкладками конденсатора, а магнитное – внутри катушки индуктивности.
Источником электромагнитных волн может быть любой колебательный контур или проводник, по которому течёт переменный ток. Однако излучающая способность источника определяется его формой, размерами и частотой колебаний. Чтобы излучение играло заметную роль, необходимо увеличить объём пространства, в котором электромагнитное поле создаётся. Поэтому для получения электромагнитных волн непригодны закрытые колебательные контуры (рис. 17), т.к. в них электрическое поле сосредоточено между обкладками конденсатора, а магнитное – внутри катушки индуктивности.
Герц в своих опытах, уменьшая число витков катушки и площадь пластин конденсатора, а также раздвигая их, совершил переход от закрытого колебательного контура к открытому колебательному контуру (вибратору Герца), представляющему собой два стержня, разделённых искровым промежутком. Колебания в такой системе поддерживаются за счёт источника э.д.с., подключённого к обкладкам конденсатора, а искровой промежуток применяется для того, чтобы увеличить разность потенциалов, до которой первоначально заряжаются обкладки.
Возможность обнаружения электромагнитных волн указывает на то, что они переносят энергию. Объёмная плотность энергии электромагнитной волны равна сумме плотностей энергий электрического и магнитного полей:
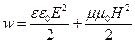 . (128)
. (128)
Учитывая выражение (127), получим, что плотности электрического и магнитного полей в каждый момент времени одинаковы, т.е. 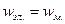 . Поэтому
. Поэтому 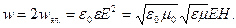
Умножив плотность энергии на скорость распространения волны в среде из формулы (126), получим плотность потока энергии, т.е. энергию, переносимую волной за единицу времени через единичную площадку, расположенную перпендикулярно к направлению распространения волны:
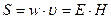 .
.
Так как векторы 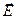 и
и 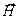 взаимно перпендикулярны и образуют с направлением распространения волны правовинтовую систему, то направление вектора
взаимно перпендикулярны и образуют с направлением распространения волны правовинтовую систему, то направление вектора 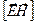 совпадает с направлением переноса энергии, а модуль этого вектора равен
совпадает с направлением переноса энергии, а модуль этого вектора равен 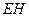 . Следовательно, вектор плотности потока электромагнитной энергии (вектор Умова-Пойнтинга):
. Следовательно, вектор плотности потока электромагнитной энергии (вектор Умова-Пойнтинга):
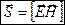 .
.
Дата добавления: 2017-12-05; просмотров: 1072;
