Магнитный вид неразрушающего контроля

2.1. Магнитное поле и его характеристики

Физическое поле существует, если на предмет, находящийся в его среде, действует сила. Например, человек массой m постоянно испытывает действие гравитационного поля: где бы он ни находился, Земля притягивает его с силой

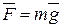, (2.19)

где 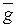– ускорение свободного падения.

Для всех физических полей структура формулы для определения силы поля одинакова. В ней всегда фигурирует произведение одной или нескольких величин, характеризующих тело (масса, заряд, скорость и т. д.), на векторную величину, которая характеризует поле в точке его местоположения. Эта величина называется напряженностью поля. В выражении (2.19) ускорение свободного падения 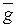есть напряженность гравитационного поля.

Рассмотрим другое по физической природе поле – электростатическое. Оно действует только на заряженные тела, обладающие зарядом q, с силой

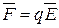, (2.20)

где 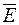– напряженность электростатического поля в месте его нахождения.

Подчеркнем, что электростатическое поле более избирательно, оно создается только заряженными телами, заряды q которых могут быть и положительными, и отрицательными, масса же m в формуле (2.19) всегда положительна. Но построение формул одно и то же: чтобы получить силу, надо определенную величину, относящуюся к телу, умножить на напряженность поля в этой точке.

Физические поля представляются силовыми линиями. Главное свойство такой линии поля состоит в том, что в любой точке, через которую она проходит, направление вектора напряженности совпадает с направлением касательной к ней в этой же точке (рис. 2.52, а). Проведя на рисунке одну силовую линию, мы уже задаем направление напряженности в бесконечном числе лежащих на ней точек. Поле сильнее, т.е. величина напряженности больше там, где линии будут расположены гуще, и слабее, где они разряжены (рис. 2.52, б). Они как «упругие нити» могут сходиться или расходиться, но пересекать друг друга не могут.

Поле, напряженность которого одинакова во всех точках, называется однородным. В противном случае оно неоднородно.

Магнитное поле – это один из видов силовых полей, но в отличие от электростатического оно еще более избирательно – действует только на движущиеся заряды. На неподвижные заряженные предметы даже в самых сильных магнитных полях не действует никакая сила. Становится очевидным, что «конструкция» формулы для определения силы, действующей на движущееся тело в магнитном поле, должна быть сложнее предыдущих.

Действительно, для гравитационного поля важна лишь масса тела m, для электрического (кулоновского) – величина его заряда q, а для магнитного важными оказываются сразу три фактора: заряд тела, численное значение и направление скорости его движения .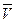

Сила, приложенная к движущемуся заряженному телу со стороны магнитного поля, называется силой Лоренца:

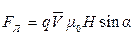, (2.21)

где α – угол между направлениями векторов скорости 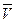и напряженности магнитного поля 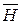в точке, где находится тело;

μ₀ – размерный коэффициент.

Напряженность магнитного поля Н – силовая величина, не зависящая от магнитных свойств среды, в которой поле существует. Она характеризует магнитное поле по величине и направлению, но учитывает влияние на интенсивность поля проводников с токами и расположение магнитов.

В системе СИ измеряется в амперах на метр – А/м. Вектор напряженности магнитного поля 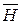можно представить, помес-

тив его в прямоугольную систему координат на поверхности де-

тали и соединив начала вектора и системы координат в виде его составляющих 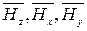(рис. 2.53). Такое представление удобно в работе, так как проще измерять не вектор в целом, а его компоненты. Особенно часто используют компоненты 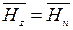– нормальный, т. е. перпендикулярный поверхности детали, и 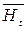– тангенциальный с модулем 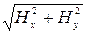, направленный параллельно поверхности.

Заменим произведение нескольких параметров, характеризующих тело в выражении (2.21), на единственный, более сложный чем масса или заряд, параметр, который называется магнитным моментом.

Как направлена сила магнитного поля? В гравитационном поле сила всегда направлена в ту же сторону, что и ускорение свободного падения, ведь тел с отрицательной массой не бывает. В электрическом поле сила 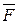и напряженность Е всегда направлены вдоль прямой, соединяющей два заряда. В магнитном поле сила Лоренца 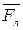всегда перпендикулярна и к напряженности 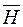, и к скорости тела 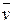. 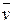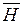Очевидно, что единственная прямая, перпендикулярная одновременно к векторам и , есть перпендикуляр к плоскости, в которой лежат эти векторы (рис. 2.54, а).

Если изменить на противоположное направление скорости 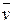или напряженности 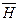, то поменяется на противоположное и направление силы 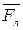. Последнее можно определить по известному правилу правой руки.

В случае, когда носителями зарядов является движущийся в проводнике поток электронов, силы Лоренца, приложенные к каждому электрону в потоке, складываясь, прижимают их к стенке провода, толкая его поперек движения электронов, т.е. перпендикулярно направлению электрического тока. В результате формула (2.21) преобразуется, и значение силы, действующей на проводник длиной l с током I, расположенный под углом α к направлению поля 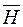(рис. 2.54, б), будет определяться законом Ампера:

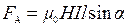. (2.22)

Если ток течет в контуре в виде плоской рамки в однородном поле Н, направленном параллельно сторонам АВ и СД (рис. 2.55, а), то возникают две силы Ампера, воздействующие перпендикулярно сторонам ВС и ДА (a = 90°), параллельные между собой и направленные противоположно, которые образуют на плече b пару сил с моментом

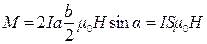, (2.23)

где 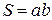– площадь рамки.

Формулу (2.23) можно представить в виде:

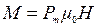, (2.24)

где величину 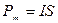называют магнитным моментом контура. Единицей измерения 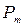является А·м² – «амперквадратный метр».

Если рассматривать плоский контур произвольной формы с током в однородном магнитном поле, то необходимо просуммировать воздействие Н на отдельные малые элементы контура, и результат останется тем же: формула (2.24) будет справедливой. Магнитному моменту 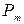контура придают векторный характер. Условились за направление 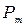принимать направление положительной нормали к контуру с током по правилу правозаходного винта.

В общем случае, когда контур с током I и однородное магнитное поле Н не лежат в одной плоскости, а находятся под углом α, который на рис. 2.55, б показан как угол между направлением поля Н и нормали ( 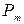) к контуру, поле Н можно разложить на две составляющие – 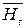и .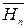

Тогда тангенциальная составляющая ( 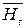) лежит в плоскости контура, а нормальная ( 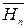) перпендикулярна ему. При этом 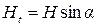и 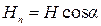. Вращающий момент создает только составляющая 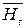, т. е.

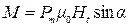, (2.25)

или в векторной форме:

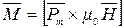. (2.26)

Для более компактного представления силового воздействия магнитного поля введем в рассмотрение магнитную индукцию 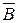, которая, как и напряженность 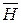, является величиной векторной и служит основной характеристикой магнитного поля. Величины 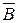и 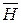связаны соотношением:

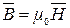. (2.27)

Здесь размерный коэффициент μ₀ в системе СИ равен 4π10^–7 Гн/м. Его называют также магнитной постоянной (проницаемостью) вакуума, придавая этим данному коэффициенту физический смысл. Тогда с учетом (2.27) выражение (2.26) можно представить в виде векторного произведения:

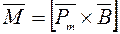, (2.28)

т. е. формула для определения силового воздействия на контур с током в магнитном поле становится такой же простой, как в гравитационном и электростатическом. Различие заключается в том, что для двух последних формулы 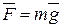, 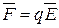определяют силы, действующие на пробное тело, а формула (2.28) – момент сил. Под действием гравитационного и электростатического поля пробное тело движется поступательно. Контур с током под действием однородного магнитного поля испытывает поворот. Под действием неоднородного поля контур одновременно и вращается и поступательно перемещается.

Вопросы, изложенные в этом разделе, рассмотрены в [49, 51].

2.2. Источники магнитного поля

Любой проводник или контур с электрическим током, так же как и движущийся электрический заряд, создают свое собственное магнитное поле. Количественную оценку такого магнитного поля производят с помощью напряженности Н (рис. 2.56, а), которая определяется законом Био-Савара-Лапласа: элемент контура 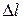, по которому течет ток силой I, создает в произвольно выбранной точке А пространства магнитное поле напряженностью

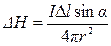, (2.29)

где r – расстояние от элемента контура 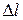до рассматриваемой точки;

α – угол между r и Δl.

Вектор напряженности магнитного поля 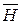, созданный током I, перпендикулярен плоскости, в которой лежат элемент Δl и отрезок r.

Рассмотрим частные, но важные для практики случаи.

Магнитное поле прямолинейного проводника с током. Суммируя все 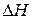от всех 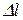, на основе уравнения (2.29) получаем:

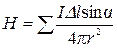. (2.30)

Согласно рис. 2.56, б имеем: 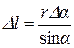и 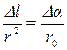. Тогда 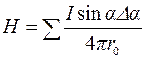. Переходя к интегрированию, получаем: .

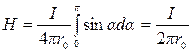Таким образом, напряженность поля Н в любой точке, расположенной на расстоянии r от оси прямолинейного проводника, определяют по формуле:

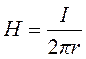. (2.31)

Силовые линии магнитного поля – это концентрические окружности с центрами на оси проводника (рис. 2.57, а). Направление поля связано с направлением тока правилом правозаходного винта. По мере приближения к оси проводника ( 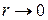) поле усиливается, а с удалением – падает, что показано на рис. 2.57, а сгущением или, соответственно, разряжением силовых линий.

Подчеркнем, что гиперболический закон (2.31) уменьшения Н верен только для точек вне проводника. Внутри проводника диаметром 2r₀ поле по мере удаления от его геометрической оси линейно возрастает с увеличением r:

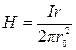. (2.32)

Таким образом, напряженность поля внутри проводника в пределах r < r₀(участок 1) 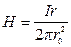, а вне – при r > r₀ (участок 2) 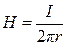(рис. 2.57, б). Напряженность в любой точке, расположенной на поверхности проводника (r = r₀), достигает максимального значения .

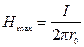Прямолинейные проводники с током в виде медных стержней или гибких кабелей различного сечения применяют для циркулярного намагничивания контролируемых деталей.

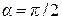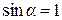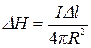Магнитное поле кругового тока. В центре кругового тока (рис. 2.58, а), когда , и , напряженность

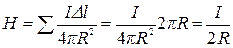, т. е. 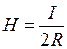. (2.33)

Магнитное поле на оси кругового тока. магнитное поле на оси кругового тока на расстоянии d от плоскости его протекания (рис. 2.58, б) можно рассчитать по формуле:

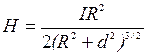. (2.34)

При d = 0 формула (2.34) переходит в выражение (2.33). С увеличением d значение напряженности поля по оси уменьшается. Если имеется w проводников, уложенных в достаточно тонкую катушку (d » 0), то в (2.34) вместо I войдет произведение wI. Длинная катушка называется соленоидом.

Магнитное поле соленоида. С учетом обозначений на рис. 2.59, на основе (2.29) выражение для поля Н (оно направлено вдоль оси соленоида) запишем в виде:

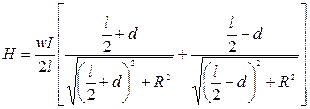. (2.35)

соотношение (2.35) применяется для расчета в магнитной дефектоскопии, так как соленоиды широко используются для намагничивания деталей.

Часто пользуются упрощенным вариантом выражения (2.35), считая соленоид бесконечно длинным, т. е., принимая 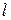>> R, имеем:

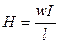. (2.36)

Поле соленоида пропорционально току I и отношению числа витков к длине соленоида 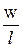, которое называют постоянной соленоида.

В центре соленоида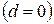

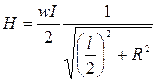, (2.37)

у края соленоида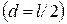

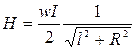. (2.38)

Если при этом l >> R, то 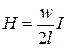, т. е. на краю длинного соленоида поле в два раза меньше, чем в середине. При R >> l выражение (2.35) переходит в (2.33) с соответствующим числом витков.

Как видно из рис. 2.59, поле будет однородным лишь внутри и вблизи центра соленоида. Приближаясь к его краям, силовые линии начинают расходиться, и напряженность поля падает. Снаружи, например, у правого конца, силовые линии «загибаются назад», рассеиваются и на входе слева сгущаются.

Магнитное поле проводника конечного сечения. В практике магнитной дефектоскопии для контроля осесимметричных деталей или деталей в форме тел вращения часто применяют циркулярное намагничивание путем пропускания тока непосредственно вдоль оси детали. При этом поле (см. рис. 2.57, б) в некоторой точке вне цилиндра, удаленной на расстояние r от центра цилиндра, рассчитывается по формуле (2.31). Так как поле внутри цилиндра создается током 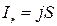, где плотность ток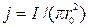а , а 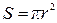, то для r << r₀ поле определяется как 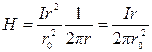, и оно, как и следовало ожидать, совпадает с полем, рассчитанным по формуле (2.32).

Таким образом,

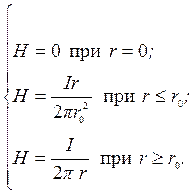(2.39)

Магнитное поле тока, текущего по трубе. Аналогичные рассуждения дают в данном случае следующие результаты по участкам 1–3 (рис. 2.60):

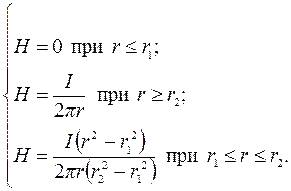(2.40)

Вопросы, изложенные в этом разделе, рассмотрены в [49, 53].