Относительные показатели
Сама по себе абсолютная величина не дает полного представления об изучаемом явлении, не показывает его структуру, соотношение между отдельными частями, развитие во времени. В ней не выявлены соотношения с другими относительными показателями. Эти функции выполняют определяемые на основе абсолютных величин относительные показатели.
Относительный показатель– это обобщающий показатель, который представляет собой результат деления одного абсолютного показателя на другой и выражает соотношение между количественными характеристиками социально-экономических процессов и явлений:
текущий / сравниваемый
показатель
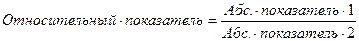
основание / база сравнения
Относительные показатели могут выражаться в коэффициентах, процентах, промилле, продецимилле или быть именованными числами. Если база сравнения принимается за 1, то относительный показатель выражается в коэффициентах, если база принимается за 100, 1000 или 10 000, то относительный показатель соответственно выражается в процентах (%), промилле (%о) и продецимилле (%оо).
Все используемые на практике относительные статистические показатели можно разделить на следующие виды:
Относительный показатель динамики(ОПД) представляет собой отношение уровня исследуемого процесса или явления в данный период времени к уровню этого же процесса или явления в прошлом и показывает, во сколько раз текущий уровень превышает предшествующий, или какую долю от него составляет:
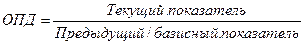
При этом если в качестве базы сравнения выбирается уровень явления в начальный момент времени (базисный), то получают базисный показатель, если в качестве базы выбирается уровень явления за предыдущий момент времени, то получают цепной показатель.
Если данный показатель выражен кратным отношением, он называется коэффициентом роста, при домножении этого коэффициента на 100% получают темп роста.
Относительный показатель планового задания (ОППЗ) рассчитывается как отношение уровня, запланированного на будущий период (yпл.), к уровню, фактически сложившемуся в прошлом (y0): 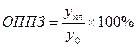
Относительный показатель реализации плана (ОПРП) – определяется как отношение фактически достигнутого уровня в текущем периоде (y1) к запланированному на этот же период (yпл.): 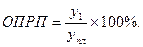
Между относительными показателями планового задания, реализации плана и динамики существует следующая взаимосвязь:
ОППЗ ´ ОПРП = ОПД.
Относительный показатель структуры (ОПС) характеризует долю или удельный вес части совокупности в общем ее объеме:
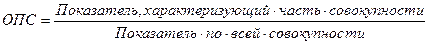
ОПС выражается простым кратным отношением (в долях единицы) или в процентах.
Относительные показатели координации(ОПК) отражают соотношение отдельных частей целого между собой:
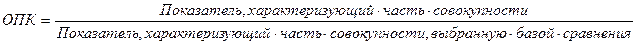 В результате определяют, сколько единиц каждой структурной части приходится на 1 единицу базисной структурной части.
В результате определяют, сколько единиц каждой структурной части приходится на 1 единицу базисной структурной части.
Относительный показатель интенсивности(ОПИ) всегда является именованной величиной и характеризует степень распространения изучаемого процесса или явления в присущей ему среде:
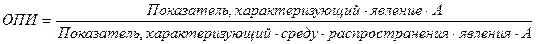
ОПИ вычисляются путем сравнения разноименных величин, находящихся в определенной связи между собой и обычно определяются в расчете на 100, 1000 и т.д. единиц изучаемой совокупности (например, число родившихся на 1000 чел. населения, производство сельскохозяйственной продукции с 1 га сельскохозяйственных угодий и т.д.).
Разновидностью ОПИ являются относительные показатели уровня экономического развития, характеризующие производство продукции в расчете на душу населения.
Относительный показатель сравнения (ОПСр) представляет собой соотношение одноименных абсолютных показателей, характеризующих разные объекты (предприятия, фирмы, районы, области, страны и т.п.), но относящиеся к одному и тому же моменту времени (например, соотношение между уровнями себестоимости одного вида продукции, выпущенной разными предприятиями):
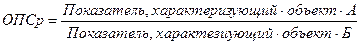
Несмотря на большую значимость относительных величин в статистике, их нельзя рассматривать в отрыве от абсолютных показателей. Лишь комплексное применение эти величин дает достоверную информацию об изучаемых явлениях или процессах.
Средние величины
При анализе и планировании необходимо опираться не на случайные факты, а на показатели, выражающие основное, типичное. Такую характеристику дают средние величины.
Средняя величина – это обобщающий показатель, характеризующий типичный уровень варьирующего признака в расчете на единицу однородной совокупности в конкретных условиях места и времени.
При расчете средней величины индивидуальные значения признака заменяются одним средним значением. При этом случайные отклонения значения признака по отдельным единицам в сторону увеличения или уменьшения взаимно уравновешиваются и погашают друг друга, а в величине средней проявляется типичный размер признака, свойственный данной группе или совокупности в целом, что позволяет выявить закономерности, присущие массовым общественным явлениям, незаметные в единичных явлениях.
Средняя величина всегда именованная, она имеет ту же единицу измерения, что и признак у отдельных единиц совокупности.
В статистике применяют две категории средних:
1. Степенные средние – средняя арифметическая, средняя гармоническая, средняя геометрическая и средняя квадратическая.
2. Структурные средние – мода и медиана.
Степенные средние
Степенные средние в зависимости от представления исходных данных могут быть простыми и взвешенными.
Простая средняя вычисляется по несгруппированным данным и имеет следующий вид:
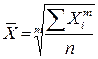 ,
,
где хi – значение признака для единицы совокупности i,
m – показатель степени средней,
n – число единиц совокупности.
Взвешенная средняя вычисляется по сгруппированным данным и имеет вид:
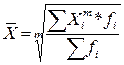 ,
,
где хi – значение признака для единицы совокупности i,
m – показатель степени средней,
fi – частота, показывающая, сколько раз встречается i-е значение признака.
Формулы расчета степенных средних имеют общий показатель степени m. В зависимости от того, какое значение он принимает, различают следующие виды степенных средних:
1. Средняя арифметическая (m=1) – наиболее распространенный вид средней.
| простая | взвешенная |
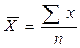
| 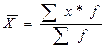
|
Примечание. Если значения осредняемого признака заданы в виде интервалов, то при расчете средней арифметической величины в качестве значений признаков в группах принимают середины этих интервалов, в результате чего образуется дискретный ряд. При этом величины открытых интервалов условно приравниваются к интервалам, примыкающим к ним.
Свойства средней арифметической:
а) если все индивидуальные значения признака (все варианты) уменьшить или увеличить в m раз, то среднее значение соответственно уменьшится или увеличится в m раз.
б) если все варианты осредняемого признака уменьшить или увеличить на число А, то средняя арифметическая соответственно уменьшится или увеличится на это же число А.
в) если частоты (веса) всех осредняемых вариантов уменьшить или увеличить в k раз, то средняя арифметическая не изменится.
2. Средняя гармоническая (m=-1) – является величиной обратной для средней арифметической и применяется, когда статистическая информация не содержит частот по отдельным вариантам совокупности, а представлена как их произведение xf.
| простая | взвешенная |
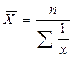
| 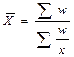 ,
где w = xf ,
где w = xf
|
3. Средняя геометрическая (m=0) – применяется для определения средней по значениям, имеющим большой разброс, либо в случаях определения средней величины по относительным показателям, например, среднегодовых темпов роста в рядах динамики, где индивидуальные значения признака представляют собой коэффициенты роста:
| простая | взвешенная |
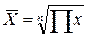
| 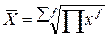
|
1. Средняя квадратическая (m=2) – применяется, когда требуется определить средний размер признака, выраженный в квадратных единицах измерения (для вычисления средней стороны квадратных участков) или при расчете среднего квадратического отклонения, являющегося одним из показателей вариации признаков:
| простая | взвешенная |
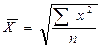
| 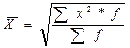
|
Если рассчитать все виды средних для одних и тех же исходных данных, то их значения окажутся неодинаковыми, т. к. здесь действует правиломажорантности средних: чем больше показатель m, тем больше средняя величина:
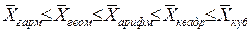 .
.
Дата добавления: 2017-11-04; просмотров: 7567;
