Показатели вариации признака
Средние величины раскрывают важную обобщающую характеристику совокупности по варьирующему признаку. Рассчитав их, необходимо уяснить, насколько они показательны, типичны или однородны. Для этого необходимо определить показатели вариации признака. Простейшей из таких характеристик может служить размах вариации,который вычисляется как разность между наибольшим и наименьшим значениями признака:
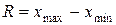 .
.
Размах вариации показывает только крайние отклонения, но не отражает отклонений от средней всех значений признака в вариационном ряду. Последнее можно получить, если рассчитать отклонения всех вариант от средней 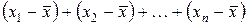 и вычислить среднюю арифметическую из всех отклонений.
и вычислить среднюю арифметическую из всех отклонений.
Известно, что сумма всех положительных (которые больше средней) и всех отрицательных (которые меньше средней) отклонений равна нулю. Поэтому при расчете средней арифметической из отклонений необходимо абстрагироваться от знаков «+» и «-». В этом случае сумма отклонений 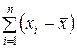 , разделенная на число отклонений
, разделенная на число отклонений 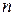 , а при наличии частот - на число
, а при наличии частот - на число 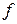 , и будет средним арифметическим отклонением. В связи с этим расчетная формула будет выглядеть следующим образом:
, и будет средним арифметическим отклонением. В связи с этим расчетная формула будет выглядеть следующим образом:
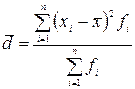 .
.
В результате мы получили среднее арифметическое (линейное) отклонение,которое обозначается символом 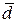 . Это втораямера измерения вариации признака.
. Это втораямера измерения вариации признака.
Среднее арифметическое (линейное) отклонение в статистическом анализе применяется редко. Обычно используют третий показатель вариации — дисперсию,или средний квадрат отклонений.Она обозначается символом 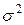 (сигма малая в квадрате) и представляет собой то же среднее арифметическое отклонение
(сигма малая в квадрате) и представляет собой то же среднее арифметическое отклонение 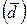 , но только отклонения возведены в квадрат, и из квадратов отклонений вычисляют среднюю величину:
, но только отклонения возведены в квадрат, и из квадратов отклонений вычисляют среднюю величину:
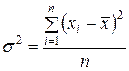 , а при наличии частот
, а при наличии частот 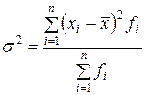 .
.
При расчете дисперсии не надо абстрагироваться от знаков (+ и -) отклонений, так как при возведении в квадрат все знаки отклонений становятся положительными.
Если извлечь корень квадратный из дисперсии, то мы получим следующий, четвертый,показатель вариации — среднее квадратическое отклонение,которое обозначается символом 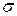 (сигма малая):
(сигма малая):
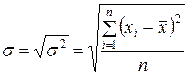 , а при наличии частот
, а при наличии частот 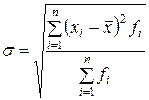 .
.
Дата добавления: 2017-10-09; просмотров: 426;
