ПОВЕРХНОСТНАЯ ЭНЕРГИЯ
Следует рассмотреть более подробно величину s на границе чистой неассоциированной жидкости с воздухом или собственным паром. С увеличением температуры наблюдается понижение s . Объясняется это тем, что межмолекулярные силы уменьшаются с увеличением среднего расстояния между молекулами, и избыток энтропии в поверхностном слое (Ss = - dF/dT) оказывается существенно положительной величиной. Следовательно, изотермический обратимый процесс образования поверхности должен идти с поглощением тепла. На языке молекулярной кинетики это означает, что при переходе молекул из объемной фазы в силовое поле поверхностного слоя уменьшается число степеней свободы их движения, кинетическая энергия, а следовательно, и температура. Происходит локальное охлаждение, аналогичное процессу перехода жидкость → пар. Для поддержания Т = const необходим подвод тепла извне. Таким образом, полная энергия образования поверхностного слоя Us больше поверхностной свободной энергии Fs . Соотношение между ними устанавливается уравнением Гиббса-Гельмгольца, которое может быть записано для удельных величин в виде
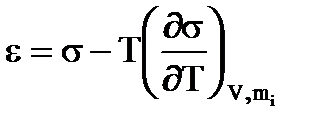, ( 9 )
где ε - полная поверхностная энергия на 1 м2 слоя (для однородной поверхности при V= const).
ХИМИЧЕСКИЙ ПОТЕНЦИАЛ И ДАВЛЕНИЕ ПАРА У ИСКРИВЛЕННЫХ ПОВЕРХНОСТЕЙ.
ТЕРМОДИНАМИЧЕСКИЕ ОСНОВЫ ОБРАЗОВАНИЯ ЗАРОДЫШЕЙ НОВОЙ ФАЗЫ
При смачивании возникают искривления поверхности, изменяющие свойства поверхностного слоя. Рассмотрим малую сферическую каплю жидкой фазы a в фазе пара b. Поскольку давление в фазе a при искривлении поверхности изменяется, можно ожидать также изменения химического потенциала m , следовательно, и давления насыщенного пара p над малой каплей, так как dm/dR¹0.
Запишем уравнение Гиббса для объемной фазы a при переменных Т и Р
;
,
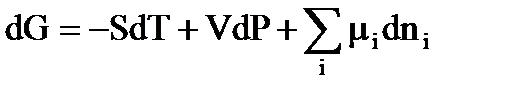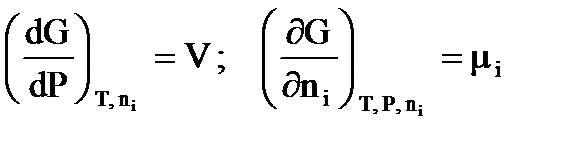где индекс ј относится ко всем компонентам, кроме ί - го.
Отсюда находим производную:
.
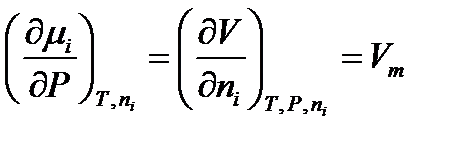В процессе образования кривизны в однокомпонентной ( ί = 1 ) двухфазной ( a, b ) системе при постоянных Т, S и n1
.
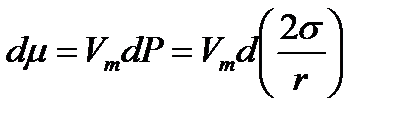Примем парциальный молярный объем жидкости Vm в первом приближении постоянным. Например, для воды при r = 10-5 см и s = 73Дж/см2, Δ R ≈ 15 106 Дж/см2 ≈ 15 атм. Эта величина мала по сравнению с внутренним давлением воды (~ 104 атм.), и поэтому справедливо допущение, что в процессе искривления поверхности дополнительного сжатия жидкости не происходит. В этом случае при интегрировании от плоской поверхности ( r = ∞ ) до искривленной ( r ) можно вынести Vm за знак интеграла:
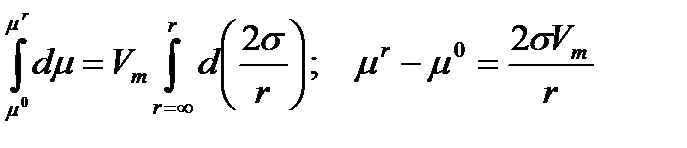, (12)
где µ0 - значение µ вещества у плоской поверхности.
Из уравнения (12) следует, что µ в капле выше чем у плоской поверхности, но в состоянии равновесия химические потенциалы жидкости и пара равны.. Тогда, относя в уравнении (12) левую часть к пару, а правую - к жидкости, можно записать для идеальной системы:
;
.
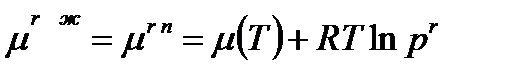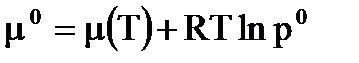Подставляя µr и µ0 в уравнение (12), получаем важное соотношение, называемое уравнением Томсона - Кельвина:
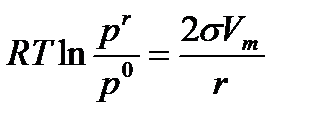(13)
Уравнение (13) показывает, что давление насыщенного пара над каплей будет тем больше, чем больше s и чем меньше радиус капли r. Например, для капли воды с радиусом r = 10-5 см ( s = 73, ῡ = 18 ) расчет дает рr/р0 = 0,01 т.е. давление увеличивается на 1 %. Для капли с r = 10-6 см рr/р0 = 1,11. Это следствие уравнения Томсона - Кельвина позволяет предсказать наблюдаемое явление изотермической перегонки, которое заключается в испарении наиболее малых капель и конденсации пара на более крупных и на плоской поверхности. Действительно, для фазы насыщенного пара, справедливо неравенство:
.
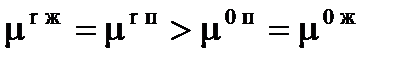Поскольку в одной фазе на одной высоте в состоянии равновесия не может быть различных значений µ, рассматриваемая система неравновесна и переход вещества должен вести к уменьшению µ: мелкие капли начнут уменьшаться вплоть до исчезновения, крупные - увеличиваться.
Над вогнутым мениском жидкости, наоборот, давление pr меньше, чем р0. В этом случае радиус кривизны меняет знак, и для сферического мениска получается уравнение:
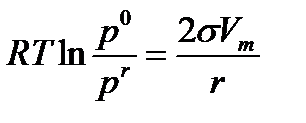. ( 14 )
Уменьшение pr над вогнутым мениском жидкости, смачивающей капилляр, также легко объяснить качественно на основе второго начала. Представим, что поднятие жидкости в капилляре достигло равновесного состояния в атмосфере насыщенного пара. Согласно барометрическому закону, давление уменьшается с высотой и pr будет тем меньше, чем больше высота поднятия, пропорциональная кривизне.
Изменение р с кривизной весьма важно в теоретическом и особенно в практическом отношении, поскольку оно затрудняет образование новой фазы, например капелек жидкости (туман) в фазе пара. При охлаждении пара уменьшается давление p и при достижении значения p0, отвечающего давлению насыщенного пара, равновесного с жидкостью, должна начинаться его конденсация. Однако, образующиеся капельки жидкости обладают, согласно уравнению (14), повышенным р > р0 , следовательно, оказываются неустойчивыми и испаряются. Для образования новой фазы ( равновесного зародыша) необходимо перенасыщение. Из уравнения (14) следует, что при r = 0, перенасыщение бесконечно, следовательно, недостижимо. Этот результат не согласуется с наблюдаемыми на практике конечными пересыщениями, приводящими к образованию капелек. Расхождение объясняется тем, что в области очень малых r (≤ 10-7 см) начинает изменяться величина s; наряду с этим и само уравнение (14) становится нестрогим. Поэтому имеет смысл говорить о размерах зародышей, равновесных с паром в условиях практического пересыщения. Такие зародыши (~ 10-6 см) образуются в гомогенной среде в результате флуктуаций. Кинетика фазового перехода, согласно теории флуктуаций, определяется уравнением
,
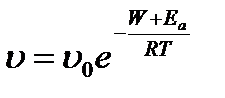где υ - скорость возникновения новой фазы; W - максимальная работа образования капли; Еа - энергия активации диффузии. Величина W является важной характеристикой фазового перехода.
Гиббс установил, что работа образования равновесного зародыша в бесконечно большой системе равна одной трети его поверхностной энергии:
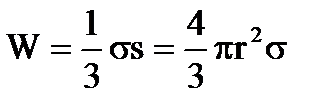. (15)
Приведенные уравнения позволяют через скорость процесса υ, обнаруживаемую практичеcки, найти равновесные значения r, следовательно, и величину пересыщения p/p0.
Высокодисперсные капельки воды, составляющие туман и облака, укрупняются в процессе изотермической перегонки, образуя капли дождя. Для облегчения конденсации пара (например, с целью искусственного дождевания) в него вводят зародыши - частицы твердой фазы (AgI и др.). Пар конденсируется на плоских гранях частиц; возникающие пленки воды оказываются устойчивыми, поскольку не обладают значительной кривизной. В атмосфере больших промышленных городов при влажности, близкой к 100%, происходит конденсация паров воды на частицах дыма и пыли. Поэтому количество осадков над городами намного превышает средние для данной местности значения.
С явлением изотермической перегонки связано образование вторичных рудных месторождений многих металлов (Cu, Zn, Cd, Ni и др.). Образующиеся в глубинных зонах земной коры (при высоких Т и Р) гидротермальные растворы сульфидов (или оксидов) этих металлов становятся при выходе в верхние зоны пересыщенными, и протекание таких растворов через участки, где имеются зерна рудных тел, приводит к росту зерен. Путем изотермической перегонки образуются также сталактиты и сталагмиты.
Рассмотрение термодинамических основ образования дисперсных систем показывает, что возникновение частиц дисперсной фазы иного агрегатного состояния (или химического состава) по сравнению с исходной маточной средой требует совершения работы, которая на одну сферическую частицу размером r описывается выражением:
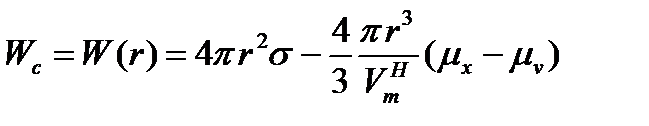, (16)
где Wc - работа образования критического зародыша, Vm - молярный объем вещества в частице, верхний индекс "н" означает новую фазу, μx и μv - химический потенциал вещества в маточной фазе и в стабильной макрофазе соответственно.
Соотношение (16) отражает тот факт, что работа образования зародыша новой фазы зависит от степени метастабильности исходной маточной фазы, т.е. от избытка химического потенциала вещества в исходной фазе μx по сравнению с его химическим потенциалом в стабильной макрофазе μv : μx - μv = - Δμ. Величина Δμ >0 характеризует степень отклонения маточной фазы от стабильного состояния (глубину внедрения в метастабильную область). Применительно к конкретным системам она может быть выражена через соответствующие термодинамические параметры (например, давление, температуру).
В выражении (16) первый член положителен и растет при увеличении r как r2, второй член может быть отрицательным (при наличии пересыщения -Δμ >0 ) и по абсолютной величине растет как r3. Поэтому, при наличии пересыщения на кривой зависимости W(r) должен существовать максимум. Этот максимум отвечает некоторому критическому размеру частицы rc - критическому зародышу новой фазы. Критический зародыш размером rc оказывается в равновесии (неустойчивом равновесии) с маточной средой, т.е. для него соблюдается условие μx - μr, где μr - химический потенциал вещества в зародыше. Для такой частицы, в соответствии с (12, 13), имеем
.
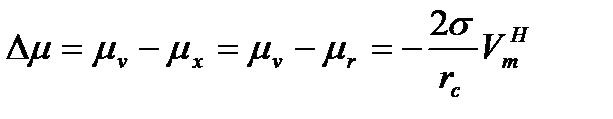Положение максимума на кривой W(r), отвечающего работе образования критического зародыша Wc, можно найти из условия равенства нулю производной по радиусу dW(r)/dr = 0 (при этом вторая производная меньше нуля d2W(r)/dr2 <0). Отсюда размер критического зародыша равен
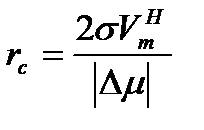. (17)
Подставляя выражение (17) в (16), приходим к уравнению, аналогичному (15)
,
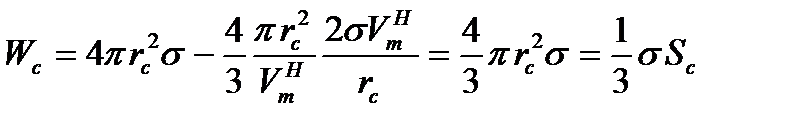где Sc - поверхность критического зародыша. Заменяя здесь величину rc на Δμ, находим
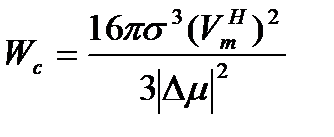. (18)
В отсутствие пересыщения (μx = μv) зависимость W(r) имеет вид параболы W(r) = 4πr2σ (рис.6) , при этом rc → ∞ и Wc → ∞. При внедрении в метастабильную область (μx > μv) на кривой W(r) появляется максимум, т.е. Wc и rc имеют конечные значения, которые уменьшаются по мере роста пересыщения /Δμ/.
Таким образом, работа образования критического зародыша Wc может рассматриваться как высота энергетического барьера, который необходимо преодолеть, чтобы реализовать возможность дальнейшего самопроизвольного роста зародышей новой фазы. Частицы с радиусом r<rc неустойчивы и исчезают, так как работа, необходимая для образования их поверхности по мере увеличения r, нарастает быстрее, чем изменение термодинамического потенциала Гиббса системы при фазовом переходе. При увеличении частиц до размеров, превышающих rc, их дальнейший рост приводит к уменьшению энергии системы: выигрыш энергии, обусловленный изменением фазового состояния новых порций вещества, компенсирует работу увеличения поверхности частицы и тем больше, чем крупнее ее размер. Поэтому такие частицы неустойчивы и самопроизвольно растут; химический потенциал вещества частицы μ падает, стремясь сравниться с химическим потенциалом вещества в макроскопической фазе.
В соответствии с уравнением (18) работа образования критического зародыша обратно пропорциональна квадрату пересыщения. Поэтому для самопроизвольного возникновения новой фазы в гомогенной системе необходимо заметное пересыщение. Наблюдавшееся часто образование новой фазы при весьма малом пересыщении и даже в его отсутствие связано с наличием посторонних включений.
2.5 МЕТОДЫ ОПРЕДЕЛЕНИЯ ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ
Величина σ может быть сравнительно легко и с большой точностью определена для легкоподвижных границ раздела фаз жидкость-газ и жидкость-жидкость.
Существующие методы определения поверхностного натяжения разделяются на три основные группы:
I. Статические методы:
1) метод капиллярного поднятия;
2) метод лежащей или висящей капли (пузырька).
II. Полустатические методы:
1) метод максимального давления образования пузырька;
2) метод отрыва кольца или рамки;
3) метод отрыва пластинки;
4) метод взвешивания и счета капель
III. Динамические методы:
1) метод капиллярных волн;
2) метод колеблющихся струй.
Статические методы основаны на изучении практически неподвижных поверхностей, находящихся в равновесии с объёмом и не изменяющихся за время измерения. Динамические методы применяются в основном для изучения существенно неравновесных состояний поверхностных слоев жидкости и скорости установления равновесной структуры их поверхности. Динамические методы основаны на том, что некоторые виды колебаний жидкости сопровождаются периодическим растяжением и сжатием её поверхности. Возвращающая сила либо частично, либо полностью обусловлена поверхностным натяжением, которое, может быть вычислено из периода колебаний.
Для границы твердое тело - газ, твердое тело - твердое тело нет прямых методов определения σ (они не могут самопроизвольно менять свою поверхность). Но косвенные указания говорят о том, что σ твердых тел больше, чем жидких.
Дата добавления: 2017-10-09; просмотров: 749;