Задания для самостоятельного решения.

I уровень

1.1. Напишите уравнения касательной и нормали к кривой 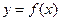в точке :

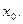1)

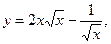
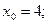
2) ,

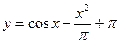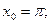
3)

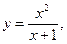
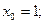
4) .

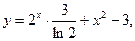
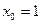1.2. Составьте уравнение касательной к графику функции 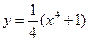в точке его пересечения с осью абсцисс.

1.3. Найдите угол, под которым график функции 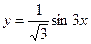пересекает ось абсцисс в начале координат.

1.4. Определите, в каких точках касательная к графику функции 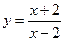образует с осью абсцисс угол .

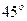1.5. Найдите, при каких значениях 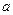парабола 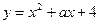касается оси абсцисс.

1.6. Тело движется по закону 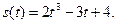Найдите скорость и ускорение тела в момент времени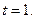

1.7. Металлический обруч катится по прямой. Угол 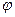поворота обруча за 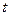секунд определяется уравнением 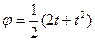. Найдите скорость и ускорение движения центра колеса.

1.8. Снаряд массой 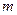выпущен вертикально вверх из зенитного орудия с начальной скоростью 50 м/с. Найдите кинетическую энергию снаряда в момент времени 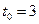. На какой высоте кинетическая энергия равна нулю?

1.9. Масса куска длины 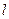неоднородного стержня вычисляется по формуле 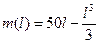. Определите, при каком значении 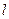плотность стержня будет втрое меньше, чем в начале стержня.

II уровень

2.1. В точке 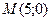проведена касательная к графику функции 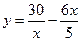. Найдите длину отрезка касательной, заключенного между осями координат.

2.2. Найдите площадь треугольника, ограниченного осями координат и касательной к графику функции 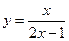в точке, ордината которой равна 1.

2.3 Дана кривая 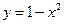. Найдите точку на этом графике, в которой касательная параллельна прямой 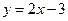и напишите уравнение нормали, проведенной в этой точке.

2.4. Касательная к параболе 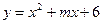проходит через начало координат. Найдите значение параметра 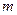, при котором абсцисса точки касания положительна, а ордината равна 8.

2.5. Напишите уравнение касательной к кривой 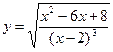в точке 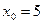. Найдите ординату точки пересечения этой касательной с прямой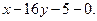

2.6. Определите, при каких значениях параметра 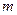прямая 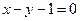является касательной к графику функции .

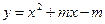2.7. К графику функции 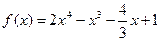в точке 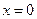проведена касательная. Найдите расстояние от начала координат до этой касательной.

2.8. К графику функции 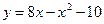проведены две касательные. Первая проводится в точке с абсциссой 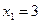, а вторая в точке, ордината которой равна 6. Найдите площадь треугольника, образованного этими касательными и осью ординат.

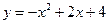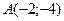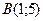2.9. Прямая пересекает параболу в двух точках и . Напишите уравнение касательной к параболе, параллельной этой секущей. Найдите угол, под которым нормаль, проведенная в точку касания, пересекает ось абсцисс.

2.10. Движения двух материальных точек по одной прямой заданы уравнениям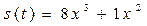и и 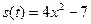. Найдите скорости движения точек в те моменты, когда пройденные ими расстояния равны.