Статистичекие сети Хопфилда
Если правила изменения состояний для бинарной сети Хопфилда заданы статистически, а не детерминированно, как в уравнении (6.1), то возникает система, имитирующая отжиг. Для ее реализации вводится вероятность изменения веса как функция от величины, на которую выход нейрона OUT превышает его порог. Пусть
Ek = NETk – qk,
где NETk – выход NET нейрона k; q – порог нейрона k, и
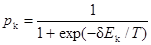 ,
,
(отметьте вероятностную функцию Больцмана в знаменателе), где Т – искусственная температура.
В стадии функционирования искусственной температуре Т приписывается большое значение, нейроны устанавливаются в начальном состоянии, определяемом входным вектором, и сети предоставляется возможность искать минимум энергии в соответствии с нижеследующей процедурой:
1. Приписать состоянию каждого нейрона с вероятностью рk значение единица, а с вероятностью 1–рk – нуль.
2. Постепенно уменьшать искусственную температуру и повторять шаг 1, пока не будет достигнуто равновесие.
Обобщенные сети
Принцип машины Больцмана может быть перенесен на сети практически любой конфигурации, хотя устойчивость не гарантируется. Для этого достаточно выбрать одно множество нейронов в качестве входов и другое множество в качестве выходов. Затем придать входному множеству значения входного вектора и предоставить сети возможность релаксировать в соответствии с описанными выше правилами 1 и 2.
Процедура обучения для такой сети, описанная в [5], состоит из следующих шагов:
1. Вычислить закрепленные вероятности.
а) придать входным и выходным нейронам значения обучающего вектора;
б) предоставить сети возможность искать равновесие;
в) записать выходные значения для всех нейронов;
г) повторить шаги от а до в для всех обучающих векторов;
д) вычислить вероятность 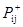 , т. е. по всему множеству обучающих векторов вычислить вероятность того, что значения обоих нейронов равны единице.
, т. е. по всему множеству обучающих векторов вычислить вероятность того, что значения обоих нейронов равны единице.
2. Вычислить незакрепленные вероятности.
а) предоставить сети возможность «свободного движения» без закрепления входов или выходов, начав со случайного состояния;
б) повторить шаг 2а много раз, регистрируя значения всех нейронов;
в) вычислить вероятность 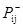 , т. е. вероятность того, что значения обоих нейронов равны единице.
, т. е. вероятность того, что значения обоих нейронов равны единице.
3. Скорректировать веса сети следующим образом:
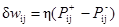 ,
,
где δwij – изменение веса wij, η – коэффициент скорости обучения.
ПРИЛОЖЕНИЯ
Дата добавления: 2017-09-19; просмотров: 407;
