Элементарная работа силы на возможном перемещении. Идеальные связи
Элементарную работу силы на возможном перемещении ее точки приложения вычисляют по обычным формулам для элементарной работы, т.е. 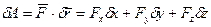 , и другим формулам для элементарной работы. Для механической системы, состоящей из
, и другим формулам для элементарной работы. Для механической системы, состоящей из 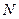 точек, к которым приложены силы, элементарная работа этих сил на каком-либо возможном перемещении системы соответственно выразится так
точек, к которым приложены силы, элементарная работа этих сил на каком-либо возможном перемещении системы соответственно выразится так
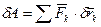 . (219)
. (219)
Элементарная работа сил при этом зависит от выбора возможного перемещения системы.
Обозначим силы реакций связей для точек системы 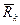 . Тогда связи системы называются идеальными, если для любого возможного перемещения системы выполняется условие
. Тогда связи системы называются идеальными, если для любого возможного перемещения системы выполняется условие
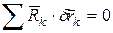 . (220)
. (220)
Условие (220) является определением идеальных связей. Важно отметить, что это условие должно выполняться для всех возможных перемещений системы. При этом вся совокупность связей является идеальной. Может быть идеальной каждая из связей в отдельности. Приведем примеры идеальных связей.
1. В абсолютно твердом теле точки связаны идеальными связями. Силами реакций связей в этом случае являются внутренние силы, для которых было доказано, что сумма элементарных работ этих сил на любых элементарных перемещениях точек тела равна нулю.
2. Абсолютно гладкая поверхность, или абсолютно гладкая линия, является идеальной связью для точки. Возможные перемещения точки с такими связями направлены по касательным к поверхности или линии. Силы реакции в этих случаях направлены по нормалям к ним, т. е. перпендикулярны силам. Так, например, все шарниры (поверхности) без трения, подвижные и неподвижные, являются связями, идеальными для тел, соединенных такими связями. Шарниры без трения, как связи идеальные, эквивалентны связям между точками в твердом теле.
3. Гибкие нерастяжимые связи типа нитей, канатов, тросов и т.п., соединяющих точки системы, являются связями идеальными. В каждом сечении такой связи силы реакций (силы натяжения) равны по модулю и противоположны по направлению, а возможные перемещения у их точек приложения одни и те же. Сумма элементарных работ сил натяжений для всех мыслимых сечений таких связей равна нулю.
4. Закрепленные точки системы по отдельности являются связями идеальными, так как их возможные перемещения равны нулю.
5. Шероховатая поверхность для катков, катящихся по ней без скольжения, при отсутствии трения качения и, следовательно, соприкосновения в одной точке или по одной линии, скорости и точек которых равны пулю, является связью идеальной. Возможные перемещения в точке или в точках линии соприкосновения равны нулю в каждый момент времени, так как равны пулю скорости в точках соприкосновения, как и для закрепленных точек.
Дата добавления: 2017-09-19; просмотров: 892;
