СТАТИКА И ТЕРМОДИНАМИКА АТМОСФЕРЫ
Основы статики атмосферы.В этом разделе изучается вывод и анализ уравнения статики атмосферы dP = -pgdz . Важно отметить, что хотя заголовок темы и предполагает отсутствие движения в атмосфере, уравнение статики справедливо и для атмосферных условий, когда имеет место движение воздуха. Наибольшее значение имеет интегрирование этого уравнения по высоте, т. е. определение вида зависимости P(z). Оно производится путем задания функции p(z) или T(z) для однородной (р (z) = const), изотермической Т(z)=const и политропной (у =– –> 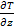 = const) атмосфер. Полная
= const) атмосфер. Полная
барометрическая формула Лапласа позволяет найти наиболее близкий к реальному вид функции P(z). Полезно обратить внимание на понятие высоты однородной атмосферы Н для различных газов, так как она зависит от молекулярного веса газа р.
Рассмотрите связь между барометрической ступенью и средней температурой внутри исследуемого слоя воздуха.
Решим несколько задач по этой теме.
Задача 1. Определить высоту однородной атмосферы сухого воздуха если Р0 = 1013,2 гПа, t = 0,0 °С. Широта места <р = 45°.
Решение. Запишем барометрическую формулу для однородной атмосферы
P2 = P,-pg(z2-z)
где P1, Р2 - давление на высотах z 1 и z 2
Приняв за верхнюю границу атмосферы ту высоту Н, где
Р2 = 0,0 гПа, найдем
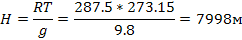
Задача 2. Найти атмосферное давление в изотермической атмосфере на высоте 8000 м, при Р0 = 1013,2 гПа, t = 0,0 °С.
Решение. Из барической формулы для изотермической атмосферы следует:
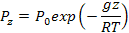
Отсюда в изотермической атмосфере на высоте 8000м Рг = 372,5 гПа.
Таким образом, атмосферное давление в изотермической атмосфере уменьшается с высотой медленнее, чем в однородной атмосфере.
Задача 3. В районе экватора (φ= 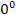 ) на двух метеорологических станциях, находящихся на разных высотах, одновременно измерены:.
) на двух метеорологических станциях, находящихся на разных высотах, одновременно измерены:.
Определить превышение верхней станции над нижней ∆z = 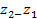 с ошибкой не более 0,3%.
с ошибкой не более 0,3%.
| Высота | t°C | РгПа | f% |
| Z1 | 22,0 | 973,5 | |
| Z2 | 16,9 | 931,4 |
Определить превышение верхней станции над нижней ∆z = 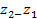 с ошибкой не более 0,3%.
с ошибкой не более 0,3%.
Решение. При использовании полной барометрической формулы в пределах тропосферы без поправки на зависимость силы тяжести от высоты, допускаемая ошибка в определении высоты станции не превысит 0,3%. Тогда
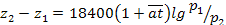
Находим:
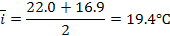
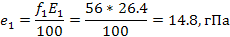
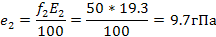
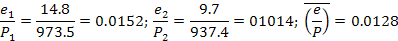
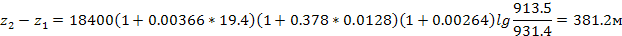
Точный ответ:
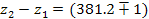
Литература
[1]-Гл. 3, § 1-7.
Вопросы для самопроверки
1. Как меняется давление воздуха с высотой? В чем физический смысл уравнения статики? Где быстрее падает давление: при подъеме на 1 км от земли или при подъеме от 2 км до 3 км? Почему?
2. Как меняется давление с высотой в однородной атмосфере? Чему равна ее высота? От чего она зависит?
3. Где располагается высота политропной атмосферы? От чего она зависит? Где располагается высота изотермической атмосферы?
4. Какие метеорологические и геофизические величины входят в полную барометрическую формулу? Как они вычисляются?
5. Рассчитайте барическую ступень и барометрический градиент у земли, если Г=273°С, 3^0= 1000 гПа.
6. Что такое градиент автоконвекции? Как меняется плотность воздуха при подъеме в атмосфере?
Основы термодинамики атмосферы. Изучение темы следует начать с вывода уравнения 1-го начала термодинамики применительно к атмосфере, хорошо понимая, что речь идет об одной из формулировок закона сохранения энергии. Простейшим процессом в термодинамике является адиабатический, когда изучаемая частица воздуха перемещается без теплообмена со средой, ее окружающей. При этом изменение теплосодержания такой частицы оказывается связанным только с пройденным ею путем вверх dz > 0, т.е. dP < 0 или вниз dz < 0 и dP > 0.
Важным является вопрос, какую температуру примет объем сухого или с ненасыщенным паром воздуха при адиабатическом перемещении. Следует учесть, что при сухоадиабатическом подъеме порции воздуха вверх, происходит работа расширения
которая совершается за счет внутренней энергии, поэтому произойдет понижение температуры этой порции. Наоборот, при опускании объема происходит переход работы сжатия во внутреннюю энергию, и опускающийся объем нагревается. Изменения температуры объема воздуха при сухоадиабатических процессах характеризуются уравнением Пуассона
: 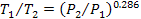
Задача 1. Какую температуру приобретет объем воздуха, имеющий температуру 17,0 °С, перемещающийся адиабатически с уровня 900,0 гПа до уровня 800,0 гПа?
Решение.
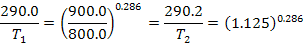
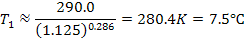
Уравнение Пуассона можно решить графически по аэрологической диаграмме. Для этого надо перемещаться по сухой адиабате (или параллельно сухой адиабате).
Задача 2. Найти температуру, которую примет воздух с ненасыщенным паром при температуре 2,7°С, если его давление адиабатически уменьшается от 970,0 до 822,0 гПа.
Р гПа
900 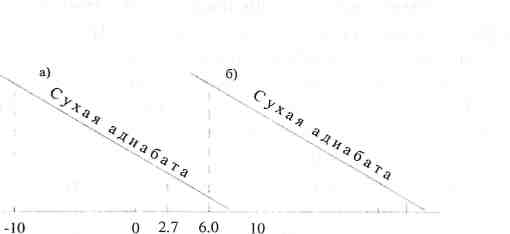
20 22.3 t°C
Рис. 1. Примеры решения задач: а - задача 2,6- задача 4
Решение. Найдите на аэрологической диаграмме точку с координатами t = 2,7 °С и Р = 970 гПа. Затем, по сухой адиабате проведите линию до Р = 822,0 гПа. Абсцисса точки с ординатой Р = 822,0 гПа является температурой воздуха (рис. 1, кривая а).
В ряде прогностических задач удобнее рассматривать изменение температуры адиабатически перемещающегося объема воздуха не с изменениями давления, а с изменениями высоты. Для этого вводится понятие суходиабатического градиента температуры (%). Он равен приблизительно 1 °С/100 м.
Задача 3. Определите, какой станет температура объема сухого воздуха, переместившегося адиабатически с вершины горы к подножью, если высота горы 1500 м, а температура объема воздуха на вершине составляла 10,0 °С.
Решение.
Т= 10°+ 1500 м- 1°С/100м=25,0°С.
Для характеристики полного запаса энергии объемов воздуха, находившихся при разных значениях давления, используют потенциальную температуру (в). Это термодинамическая температура, которую примет объем воздуха, если его суходиабатически привести к уровню Роо - 1000,0 гПа. Потенциальная температура вычисляется по формуле
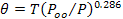
Потенциальную температуру можно приближенно вычислить по формуле:
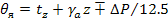
где ∆Р = Роо -Ро, Ро~ давление у поверхности земли.
Третий способ определения потенциальной температуры - графически (по аэрологической диаграмме). В этом случае из точки с координатами Г и Р следует перемещаться по сухой адиабате до изобары Р= 1000,0 гПа.
Задача 4. Определить потенциальную температуру воздуха, молекулярно-кинетическая температура которого 6,0 "С, а давление 820,0 гПа. Почему в данном случае потенциальная температура воздуха выше молекулярно-кинетической? (решение см. рис. 1, кривая б).
В результате перегрева отдельных масс воздуха в атмосфере может возникнуть конвективное движение воздуха. Ускорение, которое получит масса воздуха за счет разности силы тяжести и силы Архимеда (силы плавучести), называется ускорением конвекции:
a=g 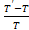
где Т' — температура объема воздуха на данном уровне; Т - температура окружающей атмосферы.
Для определения высоты уровня конвекции (уровня выравнивания температур) для воздуха с ненасыщенным паром используют формулу
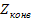 =
= 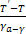
где уа - сухоадиабатический градиент; у - градиент температуры в слое атмосферы. Кроме аналитического способа, его можно найти по аэрологической диаграмме. Для этого проводят сухую адиабату от точки с координатами Р и Т' до пересечения с кривой распределения температуры в атмосфере (кривой стратификации).
Задача 5. При зондировании атмосферы получено:
| РгПа | |||||
| t°C | 15,0 | 2,0 | -6,0 | -13,0 | -20,7 |
Найти по диаграмме давление на уровне конвекции (Рконв) (выравнивание температур) и высоту этого уровня (Zконв) для единичного объема сухого воздуха, начавшего свой подъем;
а) без перегрева относительно окружающей атмосферы. На аэрологическую диаграмму наносим кривую стратификации (рис. 2).
Из точки с координатами Р = 1000 гПа, t = 15 °С проведем линию параллельно сухой адиабате до пересечения с кривой стратификации. Абсцисса точки пересечения равна 14 °С.
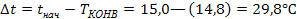
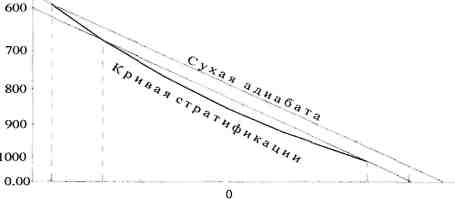
Рис. 2. Определение уровня выравнивания температур
При подъеме на 100 м температура сухого воздуха изменяется приблизительно на 1 °С. Уровень конвекции Zконв равен
Zконв=At/γa=29,& ■ 100 м= 2980 м
б) для объема воздуха, перегретого на начальном уровне на 5 °С. Наносим кривую стратификации. Если объем воздуха перегрет на величину Δt1 то начальная его температура tнач равна
tнач1— tнач1 +Δ t1
Далее, так же, как в первом случае, получаем
Zконв = 40,7 * 100 м = 4070 м.
Объем влажного воздуха с ненасыщенным водяным паром, поднимаясь вверх, тоже изменяет свое состояние по сухоадиабатическому закону. Однако, при этом в нем увеличивается относительная влажность. Высота, на которой относительная влажность становится равной 100%, называется уровнем конденсации.
Уровень конденсации по аэрологической диаграмме может быть определен, в зависимости от имеющейся информации, двумя способами:
1. Если даны температура воздуха t, давление Р, температура точки росы td, то по изограмме (линия насыщающей массовой доли водяного пара), проходящей через точку с координатами td и Р, находим Sfl ,d (массовую долю насыщенного водяного пара при температуре точки росы).
РгПа
Уровень конденсации
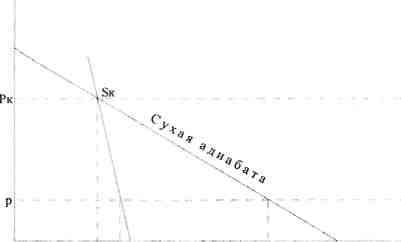
Рис. 3. Определение уровня конденсации при известной относительной влажности воздуха
Из определения точки росы следует, что SH ^=5^ (фактической массовой доле водяного пара) (рис. 3). Затем из начальной точки поднимаемся по сухой адиабате до пересечения с изограммой, равной Sф. На данном уровне водяной пар, находящийся в поднимающемся объеме, становится насыщенным. Это и есть уровень конденсации. По оси ординат определяют давление на уровне конденсации Рк, по оси абсцисс - температуру на уровне конденсации tk. По разности температур начальной и на уровне конденсации, умноженной на 100 м, определяют высоту уровня конденсации.
Задача 6. У поверхности земли температура 20,0 °С, давление 1000 гПа, точка росы 0,7 °С. Найти давление и температуру на уровне конденсации и его высоту.
Решение. Через точку с координатами tj = 0,7 °С и Р= 1000,0 гПа проходит изограмма 4 700. Из начальной точки (t = 20,0 °С, Р = 1000,0 гПа) поднимаемся по сухой адиабате до пересечения с изограммой 4 °/00. Из рис. 4 следует, что давление на уровне конденсации 750 гПа, температура -3,5 °С.
Изменение температуры при подъеме частиц от начального уровня до уровня конденсации составляет
∆t= tнач-tконв = 20,0 °С -(-3,0) °С = 23,0 °С.
Следовательно, высота уровня конденсации равна 2300 м;
2. Если даны tl, PI, f, то по изограмме, проходящей через начальную точку, определяют SH, затем из равенства Sф= SHf , (где /- относительная влажность в долях единицы) вычисляем Sф Из начальной точки поднимаемся по сухой адиабате до пересечения с изограммой, равной S
. Находим давление и температуру на уровне конденсации и по разности температур определим его высоту (как в предыдущем случае).
Задача 7. У поверхности земли температура 23,0 °С, давление 980 гПа, относительная влажность 67%. Найти давление и температуру на уровне конденсации и по разности температур определить его высоту.
Решение. Через точку с координатами Г/ = 23,0°С и Р; = 980,0 гПа проходит изограмма 18,5700. Значит SH = 18,5 700, Sф = 18,5 • 0,67 = 12,4 °/00. Из начальной точки поднимается по сухой адиабате до пересечения с изограммой 12,4 700 (рис. 6). Определяем давление на уровне конденсации. Оно равно 895 гПа. Температура на уровне конденсации 15,0°С.
∆t = 23,0 -15,0 = 8,0 °С.
Высота уровня конденсации равна 800 м.
При решении задач термодинамики атмосферы используются следующие термодинамические температуры.
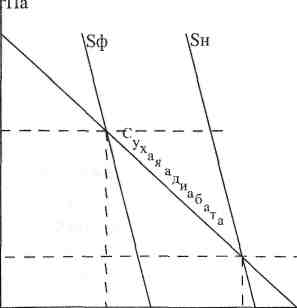
Рис. 6. Пример решения задачи №7
Эквивалентная температура t3 учитывает тепло, которое выделяется при конденсации водяного пара. Она определяется расчетным способом:
tэ = t + 2,5 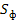 ,
,
где 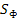 - фактическая массовая доля водяного пара. На уровне конденсации и выше уровня конденсации
- фактическая массовая доля водяного пара. На уровне конденсации и выше уровня конденсации
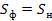
Задача 8. Давление 1022 гПа, температура 6,8 °С, относительная влажность 60%. Найти эквивалентную температуру адиабатически поднимающегося объема воздуха на уровнях: начальном, конденсации и 900 гПа.
Решение. По давлению и температуре на аэрологической диаграмме находим точку, для которой определяем насыщающую массовую долю водяного пара SH. Она составляет 6,2 700. Так как водяной пар в начальной точке не насыщен, то фактически массовая доля водяного пара составляет
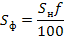
Где f- относительная влажность.
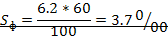
Поэтому tэ в начальной точке составляет:
tэ нач = 6,8 °С + 2,5 * 3,7 =16,0 °С.
Далее находим давление и температуру на уровне конденсации (соответственно 920 гПа и -1,5 °С). На этом уровне водяной пар в насыщенном состоянии, поэтому определенное по изограмме 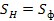
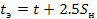
Для высоты, на которой Р = 900гПа:
tэ=-3,0 + 2,5-3,4 = 5,5°С.
Эквивалентно-потенциальная t3„ температура находится путем приведения по сухой адиабате эквивалентной температуры к давлению 1000 гПа
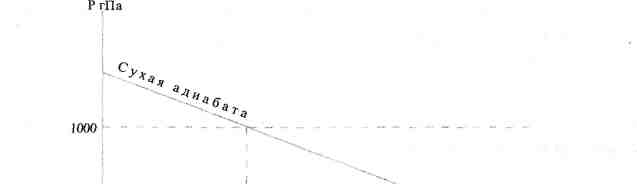
Рис. 7. Определение эквивалентно-потенциальной температуры
Задача 9. Определить эквивалентно-потенциальную температуру по данным предыдущей задачи.
Решение. На аэрологической диаграмме (рис. 7) откладываем точку с координатами ?э и Р = 1022 гПа. Затем перемещаемся по сухой адиабате до 1000 гПа. По диаграмме находим
tэn = 14.0 °С.
На уровне конденсации (920 гПа) откладываем найденную эквивалентную температуру и перемещаемся из этой точки по сухой адиабате до 1000 гПа, tm для уровня конденсации также равно 14,0 °С.
Аналогичную операцию проводим для уровня 900 гПа. На этом уровне находим t3 и перемещаемся суходиабатически до 1000 гПа ( 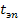 = 14,0 °С).
= 14,0 °С).
Псевдопотенциальная температура tnc - температура, которую примет воздух, если он поднимается от уровня конденсации по влажной адиабате до тех пор, пока весь пар не сконденсируется (т.е. влажная адиабата станет параллельной сухой), затем суходиабатически опускается до изобары 1000 гПа.
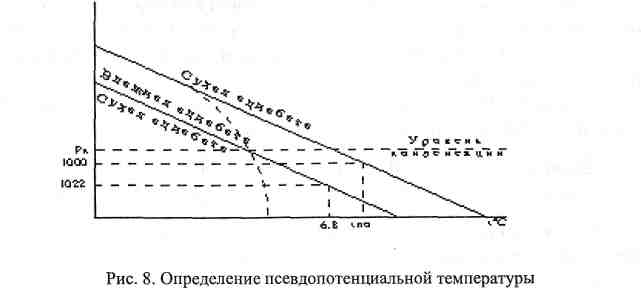
Задача 10. Определить псевдопотенциальную температуру по данным задачи 5 (см. рис. 8).
На диаграмме tnc (в К) отмечена на влажных адиабатах: tnc= 15,0 °С.
Для нахождения давления на уровне выравнивания температур (уровне конвекции) при влажноадиабатическом процессе необходимо найти точку пересечения влажной адиабаты с кривой стратификации (рис. 9).
Так как 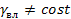 , то определить высоту уровня конвекции по способу, предложенному для сухоадиабатического процесса, нельзя. Поступим следующим образом. От уровня конденсации перемещаемся по сухой адиабате до изобарической поверхности, соответствующей уровню выравнивания температур, и определим температуру сухого воздуха на этом уровне. Найдя разность температур между начальной точкой и температурой сухого воздуха на уровне выравнивания температур (конвекции) и умножив эту разность на 100 м, получим высоту уровня конвекции.
, то определить высоту уровня конвекции по способу, предложенному для сухоадиабатического процесса, нельзя. Поступим следующим образом. От уровня конденсации перемещаемся по сухой адиабате до изобарической поверхности, соответствующей уровню выравнивания температур, и определим температуру сухого воздуха на этом уровне. Найдя разность температур между начальной точкой и температурой сухого воздуха на уровне выравнивания температур (конвекции) и умножив эту разность на 100 м, получим высоту уровня конвекции.
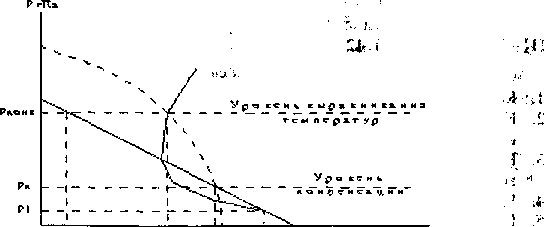
Рис. 9. Определение уровня выравнивания температур (конвекции) при влажноадиабатическом процессе.
Знание основных законов термодинамики атмосферы позволяет определить условия устойчивости атмосферы по отношению к вертикальным перемещениям сухого воздуха и воздуха, содержащего насыщенный водяной пар.
Задача 11. При зондировании атмосферы получены следующие данные о распределении температуры с высотой:
| Высота, м | ||||||
| Температура, °С | 20,0 | 18,6 | 16,6 | 15,0 | 15,0 | 13,6 |
Следует определить характер устойчивости каждого слоя по отношению к вертикальным перемещениям сухого воздуха.
Решение. В первом слое (0-100 м) имеем
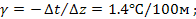
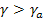
Следовательно, первый слой «сухонеустойчив». Во втором слое
у=1°с/100м; 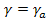
Следовательно, второй слой «сухобезразличен».
В третьем слое
у=1,6°с/200м=0,8°с/100м; 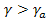
Следовательно, этот слой «сухоустойчив». Аналогично, четвертый и пятый слои также «сухоустойчивы».
Литература
[1]-Раздел 1, гл.4, § 1-12.
Вопросы для самопроверки
1. Какие характеристики газа связаны с уравнением Пуассона?
2. Как изменяется потенциальная температура адиабатически опускающегося воздуха с насыщенным паром?
3. Как изменяется массовая доля водяного пара адиабатически поднимающегося воздуха с насыщенным паром?
4. Что характеризует кривая стратификации?
5. Почему влажноадиабатический градиент меньше сухоадиабатического?
6. Какова стратификация слоя атмосферы, в котором вертикальный градиент температуры меньше влажноадиабатического?
7. Как с помощью аэрологической диаграммы оценить энергию неустойчивости?
8. Найдите с помощью аэрологической диаграммы высоту уровня конденсации, если у поверхности земли давление 900,0 гПа, температура 14,0°С и точка росы 2,2 °С.
9. Вычислите потенциальную температуру воздуха на высоте 1000 м и на уровне моря, если температура воздуха на этой высоте 10,0 °С, давление на уровне моря 950,0 гПа.
10. Какое изменение псевдопотенциальной температуры воздуха наблюдается при влажноадиабатическом процессе?
Дата добавления: 2017-09-19; просмотров: 914;
