Измеряемые характеристики моделируемых систем.

При имитационном моделировании можно измерять значения любых характеристик, интересующих исследователя. Обычно по результатам вычислений определяются характеристики всей системы, каждого потока и устройства.

Для всей системы производится подсчёт поступивших в систему заявок, полностью обслуженных и покинувших систему заявок без обслуживания по тем или иным причинам. Соотношения этих величин характеризует производительность системы при определённой рабочей нагрузке.

По каждому потоку заявок могут вычисляться времена реакций и ожидания, количества обслуженных и потерянных заявок. По каждому устройству определяется время загрузки при обслуживании одной заявки м число обслуженным устройством заявок, время простоя устройства в результате отказов и количество отказов, возникших в процессе моделирования, дины очередей и занимаемые ёмкости памяти.

При статистическом моделировании большая часть характеристик — это случайные величины. По каждой такой характеристике yопределяется N значений, по которым строится гистограмма относительных частот, вычисляется математическое ожидание, дисперсия и моменты более высокого порядка, определяются средние по времени и максимальные значения. Коэффициенты загрузки устройств вычисляются по формуле:

r_k=V_k*N_ok/T_m (1)

V_k- среднее время обслуживания одной заявки к-ым устройством;

N_ok-количество обслуженных заявок устройством за время моделирования T_m.

Определение условий удовлетворения стохастических ограничений при имитационном моделировании производится путём простого подсчёта количества измерений, вышедших и не вышедших за допустимые пределы.

6.2 Расчёт математического ожидания и дисперсии выходной характеристики.

В случае стационарного эргодического процесса функционирования системы вычисление М(у) и Д(у) выходной характеристики упроизводится усреднением не по времени, а по множеству N_знач., измеренных по одной реализации достаточной длительности. В целях экономия ОЗУ ЭВМ М(у) и Д(у) вычисляются по рекуррентным формулам:

m_n=m_n-1*(n-1)/n + y/n; (2)

где m_n-1 - математическое ожидание, вычисленное на предыдущем шаге.

d_n=d_n-1*(n-2)/(n-1) + 1/n*(y_n-m_n-1)² (3)

здесь d_n-1 - дисперсия, вычисленная на предыдущем шаге.

При большом количестве измерений эти оценки являются состоятельными и несмещёнными.

6.3 Расчёт среднего по времени значения выходной характеристики.

Например, средняя длина очереди к каждому устройству вычисляется по формуле:

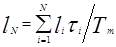(4)

где i - номер очередного изменения состояния очереди (занесение заявки в очередь или исключение из очереди); N - количество изменений состояния очереди; 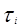- интервал времени между двумя последними изменениями очереди.

Ёмкость накопитель: 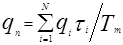(5)

где 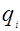- ёмкость накопителя, занятая в интервале между двумя последними обращениями к накопителю для ввода-вывода заявки.