Если , то интервал называется светоподобным, если - мнимый. , ингервал называется пространственноподобным, и при вещественном - времениподобным.

Для пространственноподобных интервалов можно всегда указать такую систему отсчета, где два события происходят одновременно.

Причинная связь между двумя событиями возможна только, если интервал между ними времениподобный.

Из инвариантности интервала следует инвариантность еще одной важной физической величины - собственного времени движущегося тела. Это понятие дает возможность построения всей цепочки мер движения в СТО, а значит и построения всей теории вообще.

Собственным временем частицы называется время, которое измеряется по часам, связанным с движущейся частицей. Для пояснения приведем простой пример: время, измеренное по часам движущейся произвольно ракеты, - это и есть собственное время ракеты (команды, находящейся в ракете).

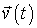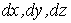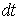Пусть мгновенная скорость частицы в некоторой ИСО I есть . В этой инерциальной системе I приращения координат и времени для частицы равны и , а в системе координат, в которой частица в данный момент покоится, приращения координат и времени суть 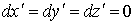и .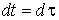

Инвариантное значение квадрата интервала представляется в виде

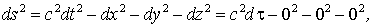
(1.12)

откуда

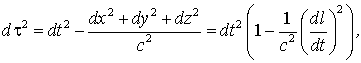
где dl - путь частицы в системе I, - мгновенная скорость частицы.

Окончательно

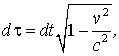
(1.13)

где V - скорость частицы в ИСО I.

Время 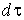- это и есть собственное время движущейся частицы. Оно измерено в системе отсчета, в которой частица неподвижна в данный момент (эта система принимается инерциальной в течение элементарного промежутка времени). Важным свойством собственного времени 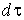есть его инвариантность при преобразованиях Лоренца, что видно из (1.12): 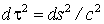. По аналогии с собственным временем собственными параметрами частицы называют их значения, измеренные в той системе отсчета, где тело покоится. К ним относятся, в частности, собственная длина и собственная масса (масса покоя). В соответствии с первым постулатом Эйнштейна эти собственные параметры одинаковы во всех ИСО.

Релятивистская динамика строится на основе постулатов Эйнштейна и их следствий - преобразований Лоренца, которые математически аккумулируют в себе метрические свойства пространства и времени. Рассмотрим способ построения релятивистской динамики по аналогии с построением ньютоновой динамики. Идея изложения заключается в построении цепочки структурно связанных величин и установлению зависимости между ними. Классическая динамика начинается с введения ряда взаимно связанных кинематических мер движения, образующих логическую цепочку, в которой каждое следующее звено определяется на основе предыдущих.

Дальше, используя понятие массы т (постоянного во всех системах отсчета параметра тела, характеризующего его инертность), вводятся динамические меры движения: 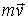- импульс, 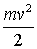-кинетическая энергия, 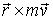- момент импульса. В продолжение, на основе понятия силы 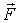вводятся меры ее действия: 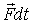- импульс силы, 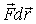- работа силы, 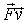- мощность силы, 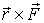- момент силы. И в заключение, на основе второго закона Ньютона, связывающего силу со скоростью изменения количества движения ( 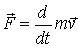), устанавливают связи между мерами действия силы и динамическими мерами движения: связь между работой и изменением кинетической энергии ( 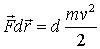), связь мощности силы со скоростью изменения кинетической энергии ( 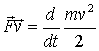), связь момента силы со скоростью изменения момента количества движения ( 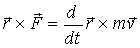). Таков путь построения динамики точки в ньютоновой механике. Аналогично будем строить и релятивистскую механику.

Четырехмерным импульсом называется величина .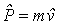

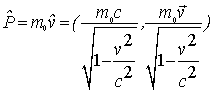
(1.14)

Сокращенно пишем 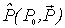, где пространственная и временная компоненты 4-импульса имеют вид

.

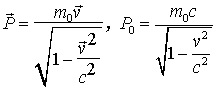(1.15)

Здесь 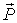- так называемый релятивистский 3-импулъс.

4-импульсу отвечает его инвариант

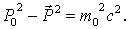
(1.16)

Как видно из этого равенства, масса покоя - 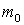- инвариант преобразований Лоренца. При небольших скоростях, когда 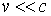, он переходит в инвариант преобразований Галилея.