Геометрии пространства

Уже в античном мире мыслители задумывались над природой и сущностью пространства и времени. Знаменитый врач и философ из города Акраганта Эмпедокл считал «пустого пространства не существует». Демокрит утверждал, что пустота существует, как материи и атомы, и необходима для их перемещений и соединений.

Пространство – это форма существования материи, характеризующаяся такими свойствами, как протяженность, структурность, сосуществование и взаимодействие. Пространство – это, прежде всего, взаимное расположение вещей и процессов друг возле друга, их протяженность и определенный поря-док взаимосвязи; оно трехмерно и обратимо.

И только в «Началах» древнегреческого математика Евклида пространственные характеристики объектов обрели строгую математическую форму. В это время зарождается геометрические представления об однородном и бесконечном пространстве.На протяжении двух тысячелетий не один математик высказывал сомнение в физической истинности аксиомы Евклида о параллельных, которая гласит:

Если две прямые пересечены третьей, то они пересекаются в той полуплоскости относительно секущей, где сумма односторонних внутренних углов меньше двух прямых. (Знаменитый пятый постулат).

Это означает, что если углы 1 и 2 в сумме меньше 180⁰, то прямые а и b, будучи продолженными достаточно далеко пересекутся (на рисунке – справа). Евклид имел достаточно веские основания, чтобы сформулировать свою аксиому именно так. Он мог бы утверждать, что если сумма углов 1 и 2 равна 180⁰, то прямые а и b никогда не пересекутся, сколько бы их не продолжали, т.е. что прямые а и b в этом случае параллельны.

Пятый постулат оказался самым проблемным, в другой формулировке он гласит:

из одной точки на плоскости можно провести только одну прямую, которая не будет пересекаться с данной, сколько бы ее ни продолжали.

Евклид явно опасался предположить, что могут существовать две бесконечные прямые, которые никогда не пересекутся. Существование таких прямых не подкреплялось опытом и отнюдь не было самоочевидным. Т.е. этот постулат не был очевиден, так как никто не мог бы его экспериментально подтвердить даже в воображении – нельзя же линию продолжать в бесконечность.

Но на основе аксиомы о параллельных и других аксиом своей геометрии Евклид доказал существование бесконечных протяженных параллельных прямых.

Самого Евклида придуманный им вариант аксиомы о параллельных не устраивал. После Евклида не один десяток самых выдающихся математиков, не говоря уже о менее известных, пытались заменить аксиому о параллельных и вывести ее из других аксиом.

С геометрией Евклида связывался тот взгляд, что пространство везде одно и то же. Она исходила из пяти аксиом или постулатов. Как уже известно, многих математиков не удовлетворял пятый постулат, который гласил, что из одной точки на плоскости можно провести только одну прямую, которая не будет пересекаться с данной, сколько бы ее ни продолжали. Этот постулат не был очевиден.

Великий математик Карл Фридрих Гаусс (1777 – 1855) первым признал пятый постулат аксиомой и что, его можно заменить другими аксиомами, построив новую геометрию. Начиная с 1833 г. К. Гаусс разрабатывал свой вариант неевклидовой (астральной) геометрии. В письме к математику и астроному Фридриху Вильгельму Бесселю (1784 – 1846) признавался, что вряд ли когда-нибудь опубликует свои открытия в области неевклидовой геометрии из опасения насмешек, или, как выразился Гаусс, криков беотийцев (в переносном смысле – невежд).

И лишь Николай Иванович Лобачевский (1793 – 1856) в России, Янош Бойаи (1802 – 1860) в Венгрии и Георг Бернхард Риман (1826 – 1866) в Германии (ученик К. Гаусса) построили новую геометрию, заменив пятый постулат.

Б. Риман заменил его на аксиому: через точку, лежащую вне данной прямой на плоскости, нельзя провести ни одной параллельной, все они будут пересекаться с данной.

Н.И. Лобачевский и Я. Бойаи допустили, что … существует множество прямых, которые не пересекутся с данной.

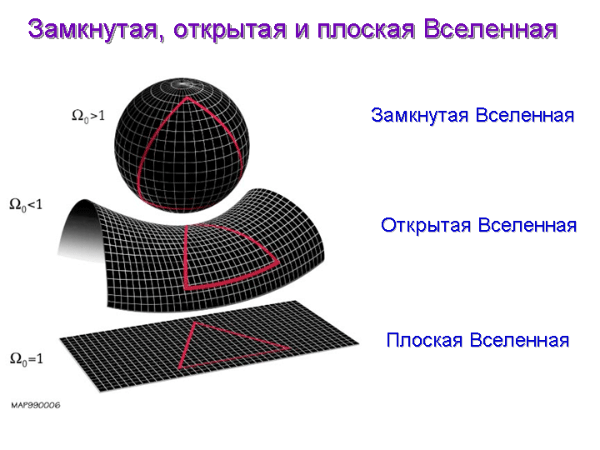
Для наглядной иллюстрации этих геометрий рассмотрим пространство двух измерений, называемое поверхностью. Евклидова геометрия реализуется на плоскости, Римана – на поверхности сферы, Лобачевского – на так называемой псевдосфере (отрицательной сфере).

Построим фигуру «треугольник» на этих трех поверхностях.

1 2 3

В геометрии Евклида сумма углов треугольника равна 180⁰, у Римана – больше 180⁰, а у Лобачевского – меньше 180^ (рис. 1, 2, 3).

Вообще, пространство имеет три измерения, для каждая геометрии характерна своя кривизна пространства: в евклидовой геометрии кривизна нулевая, у Римана – положительная, у Лобачевского – Бойая – отрицательная.

Кривизна пространства понимается в науке как отступление его метрики от евклидовой, что точно описывается в языке математики, но не проявляется каким-то наглядным образом.

Лобачевский и Риман считали, что только физические эксперименты могут показать нам, какова геометрия нашего мира. Эйнштейн в общей теории относительности сделала геометрию физической экспериментальной наукой, которая подтвердила характер пространства Римана. Общая теория относительности заменяет закон тяготения Ньютона новыми уравнениями тяготения и закон Ньютона становиться предельным случаем эйнштейновских уравнений.

Интересен ответ А. Эйнштейна корреспонденту американской газеты «Нью-Йорк Таймс». На вопрос: в чем суть его теории относительности, Эйнштейн ответил: «Суть такова: раньше считали, что если каким-нибудь чудом все материальные вещи исчезли бы вдруг, то пространство и время остались бы. Согласно же теории относительности вместе с вещами исчезли бы и пространство, и время».