Показатели оценки уровня проектных рисков.

Понимание риска как возможности отклонения от цели предполагает использование для его измерения известные в статистике показатели разброса случайной величины – дисперсию, среднеквадратическое отклонение и коэффициент вариации. Величину же разброса с характерным (ожидаемым) значением величины соразмеряет коэффициент вариации.

Показатель дисперсии:

,

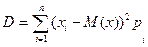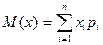
где x_i – значение неопределенного параметра в соответствии с i-тым сценарием;

М(х)- математическое ожидание неопределенного параметра;

p_i – вероятность реализации сценария i.

Показатель среднеквадратического отклонения:

.

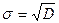Коэффициент вариации:

.

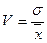Однако гипотеза о нормальном распределении некоторых экономических величин, для которых разработаны и успешно применяются вышеназванные показатели являются лишь приближением к тем видам распределений, которые встречаются в практических исследованиях, так как значительное количество параметров рынка имеют скошенное распределение вероятностей.

Существует несколько подходов к количественной оценке инвестиционного риска (разброса), связанного с изменением случайной величины, функция плотности вероятности которых имеется существенную скошенность. Вследствие того, что максимум функции плотности вероятности достигается при модальном значении случайной величины, именно модальное значение, а не математическое ожидание рассматривается здесь в качестве нового «центра» распределения. Приведенный коэффициент вариации является «передвинутым» традиционным коэффициентом вариации на величину, равную разнице математического ожидания и модального значения m, отнесенной к математическому ожиданию:

,

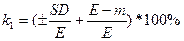где SD – показатель стандартного отклонения;

Е – показатель математического ожидания;

m – мода.

Уровень риска, рассчитанный как полудисперсия (SV_r) имеет вид:

,

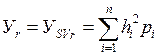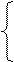
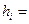
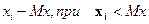
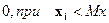
где х_i – значения случайной величины,

Mx – математическое ожидание случайной величины;

p_i – вероятность достижения случайной величиной определенного значения.

Соответственно, полуотклонение покажет среднее левостороннее отклонение от ожидаемого результата или величину разброса в худшую сторону.

Для предприятия при оценке уровня инвестиционного риска особый интерес представляет предельный уровень риска, а именно, величина, которую не превысят потери с определенной степенью вероятности. Последняя при этом задается предприятием и приобретает характер «доверительной вероятности» или «интервала доверия». Данный показатель в настоящее время широко используется зарубежными финансово-кредитными институтами как показатель «рисковой стоимости» или «стоимости под риском» (VaR – Value at Risk). Преимуществом его является то, что инвестор может отразить свое отношение к риску, выбрав тот или иной интервал доверия. Так, в наиболее простом случае, когда фактическое распределение вероятностей случайной величины приближается к нормальному, с вероятностью 95% можно утверждать, что предельные потери не превысят значения Мх – 1.65σ, с вероятностью 97.5% - не превысят значения Мх – 2σ и т.д.

При неизвестном распределении вероятностей, для нахождения предельного уровня инвестиционного риска воспользуемся неравенством Чебышева, основанном на закономерностях монотонной связи между стандартным отклонением (σ) и вероятностью того, что уровень потерь превысит какую-то величину. Тогда предельный уровень риска (У_предел) будет равен:

,

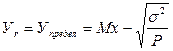где σ² – дисперсия случайной величины;

Р – заданный ПХС интервал доверия.

С помощью определенных преобразований данного показателя, можно вывести более точные значения предельного уровня риска. Так, если известно, что кривая распределения вероятностей случайной величины является симметричной относительно своего математического ожидания, то предельный уровень риска будет равен:

.

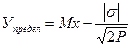Если при этом известно, что имеется только одно значение случайной величины с максимальным уровнем вероятности, то предельный уровень риска составит:

.

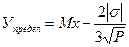Если же кривая распределения вероятностей не является симметричной относительно своего математического ожидания, то предельный уровень риска составит:

,

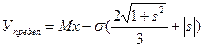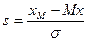
где s – пирсоновская мера асимметрии,

х_М – мода.

Отметим, что одним из недостатков показателя У_предел является необходимость в большом объеме статистической информации. Однако преимущество его экономической обоснованности, а также возможность разрешения проблемы статистической оценки с помощью экспертных методов задания функции распределения вероятностей являются важным основанием в целесообразности использования данного показателя.