Statistical Estimates of parameters of random variables distribution. Check of hypotheses
The statistical hypothesis is a certain assumption of the distribution of probabilities which is the cornerstone of observed selection of data.
Check of a statistical hypothesis is a decision making process about whether the considered statistical hypothesis contradicts observed selection of data. The statistical test or statistical criterion — the strict mathematical rule by which the statistical hypothesis is accepted or rejected.
Статистические оценки параметров распределения случайных величин. Проверка гипотез
Статистическая гипотеза определенное предположение о распределении вероятностей, которая является краеугольным камнем наблюдаемого выбора данных.
Проверка статистической гипотезы является процесс принятия решений о том, не противоречит ли рассматриваемая статистическая гипотеза наблюдаемую выборку данных. Статистический тест или статистический критерий - строгое математическое правило, по которому статистическая гипотеза принимается или отклоняется.
The statistical hypothesis represents some assumption of the law of distribution of a random variable or of parameters of this law formulated on the basis of selection. Examples of statistical hypotheses are assumptions: general set is distributed under the exponential law; population means of two exponential distributed selections are equal each other. In the first of them the assumption of a distribution law type, and in the second – about parameters of two distributions is stated. A hypothesis at the heart of which there are no assumptions about a specific type of the distribution law call nonparametric, otherwise – parametrical.
Статистическая гипотеза представляет собой некоторое предположение о законе распределения случайной величины или параметров этого закона, сформулированного на основе отбора. Примеры статистических гипотез предположения: общий набор распределяется по экспоненциальному закону; населения посредством двух экспоненциальных распределенных выбора равны друг другу. В первом из них предположение о типе закона распределения, а во втором - о параметрах двух распределений говорится. Гипотеза, в основе которого нет никаких предположений о конкретном типе закона распределения вызова непараметрического, в противном случае - параметрический.
The hypothesis claiming that distinction between the compared characteristics is absent, and observed deviations are explained only by accidental fluctuations in selections based on which comparison is made, call a zero (main) hypothesis and designate H0. Along with a main hypothesis consider also alternative (competing, contradicting) it H1 hypothesis. And if the zero hypothesis is rejected, then the alternative hypothesis will take place.
Гипотеза утверждает, что различие между сравниваемыми характеристиками отсутствует, а наблюдаемые отклонения объясняются лишь случайными колебаниями выборов, на основании которых производится сравнение, вызов (основной) гипотезу о нулевой и обозначают H0. Наряду с основной гипотезы также рассмотреть альтернативные (конкурируя, что противоречит) это H1 гипотезу. И если нулевая гипотеза отвергается, то альтернативная гипотеза будет иметь место.
Differentiate simple and difficult hypotheses. A hypothesis call simple if it unambiguously characterizes the parameter of distribution of a random variable. For example, if l is the parameter of exponential distribution, then H0 hypothesis of equality of l =10 – a simple hypothesis. Complex hypothesis which consists of a final or infinite set of simple hypotheses. The complex hypothesis of H0 of inequality l>0 consists of an infinite set of simple hypotheses of H0 of equality of l =bi where bi – any number, bigger 10. H0 hypothesis that the population mean of normal distribution is equal to two in case of unknown dispersion is difficult too. The assumption of distribution of a random variable X in normal way to the law if specific values of population mean and dispersion aren't fixed will be a complex hypothesis.
Дифференцировать простых и сложных гипотез. Гипотеза вызова простой, если она однозначно характеризует параметр распределения случайной величины. Например, если является параметр экспоненциального распределения, то H0 гипотеза о равенстве = 10 - простая гипотеза. Комплексная гипотеза, которая состоит из конечного или бесконечного множества простых гипотез. Комплексная гипотеза H0 неравенства 0 состоит из бесконечного множества простых гипотез H0 равенства = би, где би - любое число, большее 10. H0 гипотеза о том, что среднее население нормального распределения равно двум в случае неизвестной дисперсии трудно тоже. Предположение о распределении случайной величины X в обычном порядке к закону, если конкретные значения средней численности и дисперсии не являются фиксированными будет сложной гипотезы.
Check of a hypothesis is based on calculation of some random variable – criterion which exact or approximate distribution is known. Let's designate this value z=z(x1, x2, …, xn). The procedure of check of a hypothesis orders to each value of criterion one or the other of decisions
– to accept or reject a hypothesis. Thereby all selective space and respectively a set of values of criterion are divided into two not crossed subsets of S0 and S1. If value of criterion of z gets to the S0 area, then the hypothesis is accepted and if to the S1 area, – the hypothesis deviates. The set of S0 is called the field of acceptance of a hypothesis or area of admissible values, and a set of S1 – area of a deviation of a hypothesis or critical area. The choice of one area unambiguously defines also other area.
Проверка гипотезы основывается на вычислении некоторой случайной величины - критерия, точное или приближенное распределение известно. Обозначим это значение г = г (x1, x2, ..., хп). Процедура проверки гипотезы заказов каждому значению критерия одного или другого из решений
- Принять или отвергнуть гипотезу. Тем самым все избирательное пространство и, соответственно, множество значений критерия разделяются на два не пересекающихся подмножеств S0 и S1. Если значение критерия г попадает в область S0, то гипотеза принимается, и если в области S1, - гипотеза отклоняется. Множество S0 называется полем принятия гипотезы или области допустимых значений, и набор S1 - площадь отклонения гипотезы или критической области. Выбор одной области однозначно определяет также другую область.
Acceptance or deviation of a hypothesis of H0 on casual selection corresponds to the truth with some probability and, respectively, two sorts of errors are possible. The error of the first sort arises with probability of a when the right hypothesis of H0 is rejected and the competing H1 hypothesis is accepted. The error of the second sort arises with probability of b in that case when the incorrect hypothesis of H0 while the competing H1 hypothesis is fair is accepted. The confidential probability is a probability not to make a error of the first sort and to accept a right hypothesis of H0. The probability to reject a false hypothesis of H0 is called criterion power. Therefore, when checking a hypothesis four options of outcomes, the table are possible. 5.1.
Принятие или отклонение гипотезы Н0 о случайном выборе соответствует истине с некоторой вероятностью и, соответственно, два вида возможны ошибки. Ошибка первого рода возникает с вероятностью , когда правая гипотеза Н0 отвергается и конкурирующий H1 гипотеза принимается. Ошибка второго рода возникает с вероятностью в том случае, когда неверную гипотезу H0 в то время как конкурирующие гипотезы H1 справедливо принимается. Доверительной вероятности вероятность того, чтобы не сделать ошибки первого рода и принять правильную гипотезу H0. Вероятность того, чтобы отклонить ложный гипотеза Н0 называется критерием мощности. Поэтому при проверке гипотезу четыре варианта результатов, таблица возможны. 5.1.
Table 5.1
Four options of outcomes
  Hypothesis Н0 Hypothesis Н0
| Решение | Probability | Note |
| Right | accepted | 1–a | Confidence probability |
| rejected | a | The probability of a type I error |





| |||
| No right | accepted | a | The probability of a type 2error |
| rejected | 1–a | Power of a test |
For example, we will consider a case when some not displaced Estimate of the q parameter is calculated on selection of volume n, and this Estimate has density of distribution of f (q), the drawing. 5.1.
Например, рассмотрим случай, когда некоторые из них не смещаются оценка параметра вычисляется по выбору объема п, и эта оценка имеет плотность распределения F (), чертеж. 5.1.
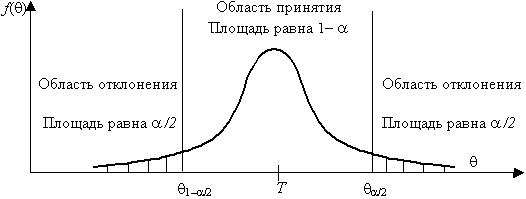
Figure 5.1 - Areas and deviations of a hypothesis
Рисунок 5.1 - Области и отклонения гипотезы
Let's assume that true value of the estimated parameter is equal to T. If to consider H0 hypothesis of equality of q = T, then, distinction between q and T has to be how big that to reject this hypothesis. It is possible to answer the matter in statistical sense, considering probability of achievement of some set difference between q and T on the basis of selective distribution of the q parameter.
Давайте предположим, что истинное значение оцениваемого параметра равно Т. Если рассмотреть H0 гипотезу о равенстве = Т, то различие между и T должно быть, насколько велика, что отвергнуть эту гипотезу. Можно ответить на этот вопрос в статистическом смысле, принимая во внимание вероятность достижения некоторой разности между заданной и Т на основе выборочного распределения параметра .
It is expedient to believe identical values of probability of an exit of the q parameter out of the lower and top limits of an interval. Such assumption in many cases allows to minimize a confidential interval, i.e. to increase the power of criterion of check. The total probability that the q parameter will go beyond an interval with borders of q1-a/2 and qa/2 makes the value a. This size should be chosen so small that an exit out of limits of an interval was improbable. If Estimate of parameter has got to the set interval, then in that case there are no bases to call in question the checked hypothesis, therefore, a hypothesis of equality of q = T can be accepted. But if after receiving selection it turns out that Estimate goes beyond the set limits, then in this case there are serious reasons to reject H0 hypothesis. From this it follows that the probability to make a error of the first sort is equal to a (it is equal to significance value of criterion).
Целесообразно полагать одинаковые значения вероятности выхода параметра из нижнего и верхнего пределов интервала. Такое предположение во многих случаях позволяет минимизировать доверительный интервал, т.е., чтобы увеличить мощность критерия проверки. Полная вероятность, что параметр будет выходить за пределы интервала с границами 1- / 2 и / 2 составляет значение . Этот размер должен быть выбран настолько мал, что выход из пределов интервала было маловероятно. Если Оценка параметра попал в заданный интервал времени, то в этом случае нет никаких оснований ставить под сомнение гипотезу проверили, следовательно, гипотеза о равенстве = Т может быть принято. Но если после получения выбора, то получается, что оценка выходит за установленные пределы, то в этом случае есть серьезные основания для отклонения H0 гипотезу. Отсюда следует, что вероятность того, чтобы сделать ошибки первого рода равна (она равна значимости значение критерия).
If to assume, for example, that true value of parameter is actually equal to T+d, then according to H0 hypothesis of equality of q = T – the probability that Estimate of the q parameter will get to the field of acceptance of a hypothesis, will make b, the figure 5.2.
Если предположить, например, что истинное значение параметра фактически равна T + D, то согласно H0 гипотезе равенства = Т - вероятность того, что оценка параметра будет добраться до области принятия гипотезы , составит , рисунок 5.2.
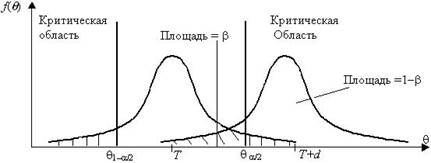
Figure 5.2. Distribution of areas
In case of the set selection amount the probability of making of an error of the first sort can be reduced, reducing significance value of a. However at the same time the probability of an
error of the second sort b increases (power of criterion decreases). Similar reasonings can be carried out for a case when the true parameter value is equal to T – d.
В случае выбора количества набора вероятность сделать ошибки первого рода может быть уменьшено, уменьшение значения значимости . Тем не менее, в то же время вероятность
ошибки второго рода возрастает (мощность критерия уменьшается). Аналогичные рассуждения могут быть проведены для случая, когда истинное значение параметра равно Т - Д.
The only way to reduce both probabilities consists in increase in amount of selection (distribution density of Estimate of parameter at the same time becomes "narrower"). In case of the choice of critical area are guided by rule of Neumann – Pearson: it is necessary to choose so critical area that the probability of a was small if the hypothesis is right, and it is big otherwise. However the choice of specific a value is rather any. Common values lie ranging from 0,001 to
q1-a/2 and qa/2 for standard a values and various methods of creation of criterion are constituted. In case of the choice of significance value it is necessary to consider capacity of criterion in
case of an alternative hypothesis.
Единственный способ свести обе вероятности заключается в увеличении количества выбора (плотности распределения Эстимейт параметра в то же время становится "узким"). В случае выбора критической области руководствуются правилом Неймана - Пирсона: необходимо выбрать так критическую зону, что вероятность была мала, если гипотеза верна, и это большая иначе. Однако выбор конкретного значения является довольно любой. Общие ценности лежат в пределах от 0,001 до1- / 2 и / 2 для стандартных значений и различных методов создания критерия состоят. В случае выбора значения значимости, необходимо рассмотреть вопрос о способности критерия при
Случай альтернативной гипотезы.
Depending on essence of the checked hypothesis and the used characteristic Estimate discrepancy measures from its theoretical value apply various criteria. For check of hypotheses of laws of distribution refer criteria to number of the most often applied criteria Pearson, Kolmogorov, Mises, Vilkokson's chi-square, about parameter values – Fischer, Student's criteria.
Let's consider a practical technique of use of a method statistical Estimate of parameters of distribution. The solvent and not displaced estimates of key parameters of distribution of the random variable (RV) (population mean of MX and dispersion σХ2) can be received on formulas:
В зависимости от сущности проверяемой гипотезы и используемых характерных мер Эстимейт несоответствие от теоретической величины применяются различные критерии. Для проверки гипотез законов распределения относятся критерии к числу наиболее часто применяемых критериев Пирсона, Колмогорова, Мизеса, хи-квадрат Vilkokson, около значений параметров - Фишера, критерия Стьюдента.
Давайте рассмотрим практический метод использования метода статистической оценки параметров распределения. Растворитель и не смещаются оценки ключевых параметров распределения случайной величины (RV) (математическое ожидание МХ и дисперсии σХ2) могут быть получены по формулам:
| n | n | |||||||||||
| е | ||||||||||||
| X | = | Ч | i =1 | X i | (5.5) | |||||||
| n | ||||||||||||
| s X 2= | Ч | е | ( X i - | )2 | (5.6) | |||||||
| X | ||||||||||||
| n - | ||||||||||||
| i =1 | ||||||||||||
| where n - selection amount. |
The sizes X and Y determine correlation coefficient Estimate between accidental by a formula:
| n | |||||||||
| е( X i - | |||||||||
| X | ) Ч (Yi - Y | ) | (5.7) | ||||||
| R XY = | Ч | i=1 | |||||||
| n - 1 | s X ЧsY | ||||||||
As estimates (5.5) - (5.6) determine by selection of final amount, there is a question of their statistical reliability and accuracy.
Let's designate θ as Estimate of the parameter interesting us. Then the task of determination of reliability and accuracy of Estimate comes down to determination of such interval (θ1, θ2) including parameter θ that with probability 1 - α (where α - rather small size equal 0.1, 0.05, 0.01 …) can be approved that the unknown true parameter value is in this interval. An interval (θ1, θ2) call a confidential interval, and probability 1-α confidential probability.
Let's consider a case when size X has the normal distribution law with a probability density:
По оценкам (5.5) - (5.6) определяют путем подбора итоговой суммы, возникает вопрос об их статистической надежности и точности.
Обозначим & thetas как оценка параметра интересующей нас. Тогда задача определения надежности и точности Эстимейт сводится к определению такого интервала (б1, в2), включая параметр & thetas, что с вероятностью 1 - а (где α - сравнительно небольшой размер равен 0,1, 0,05, 0,01 ...) могут быть утверждены что неизвестное истинное значение параметра в этом интервале. Интервал (θ1, θ2) вызвать доверительный интервал, и вероятность 1-α доверительной вероятности.
Рассмотрим случай, когда размер X имеет нормальный закон распределения с плотностью вероятности:
| - | ( X - M x ) 2 | (5.8) | ||||||
| f(x) = | Ч e | 2*s X | ||||||
| s XЧ | ||||||||
| 2p |
Confidential interval for population mean:
Доверительный интервал для среднего населения:
X - e, X + e the including Mx with probability 1-α, is found from a condition:

 P[ X - e < M X < X + e]=1- a
P[ X - e < M X < X + e]=1- a


which can be presented in the form:
(5.9)
Let's enter parameter:
| t = [(X | - M x )/s X ]Ч | (5.10) | |
| n |

Styyudenta having t-distribution with v = n - 1 degrees of freedom. Then equality (3.4) will correspond in a type:
| й | s | X | щ | (5.11) | ||||||
| P = к | X - M X | < t(a, v)Ч |
Дата добавления: 2017-05-18; просмотров: 1086;
