Coefficient of correlation of Pearson

The coefficient of correlation of Pearson of r, that is a dimensionless index in an interval from - 1,0 to 1,0 inclusive,reflects the degree of linear dependence between two great numbers of data.
The index of crowd conditions of connection between two signs is determined on the formula of linear coefficient of correlation

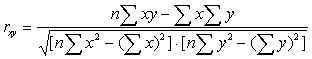
where x is a value of factor sign;

y is a value of effective sign;

n is a number of pairs of data.

Pair correlation is connection between two signs: effective and factor or two factor.

Variants are connections, characterizing a presence or absence of linear connection between signs:

-large values from one set of data are related to the large values of other set (cross-correlation) is a presence of direct linear connection;
-the small values of one set are related to the large value so the r (negative correlation) is a presence negative linear

· small values ​​of one set are associated with large values ​​of the other (negative correlation) - the presence of a negative linear relationship;

• data from the two ranges are not related (zero correlation.) - No linear relationship data

• two ranges are related (zero correlation) - no linear relationship.

As an example, take a data set A (Table 7). It is necessary to determine the presence of a linear relationship between the signs of x and y.

For a graphical representation of relationship between two variables used coordinate system with the axes corresponding to the variables x and y. Construction schedule called dispersion diagram is shown in Fig. 6. This diagram shows that the low value of the variable x correspond to low values ​​of the variable y, the high value of the variable x correspond to high values ​​of the variable y. This example demonstrates the clear relationship.

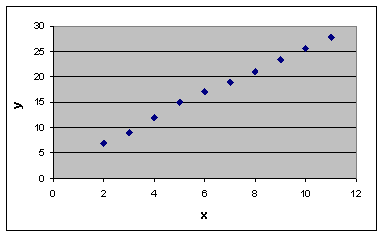
Figure4- scatter plot

Thus, we can establish a relationship between the variables x and y. We calculate the Pearson correlation coefficient between two arrays (x, y) using MS Excel Pearson (Array1, array2) function. The result is the value of the correlation coefficient is equal to 0.998364, the relationship between the variables x and y, is very high. With the help of MS Excel analysis package, as well as an analysis tool "Correlation", we can construct the correlation matrix.

Any relationship between the variables have two important characteristics: size and reliability. The stronger the relationship between two variables, the greater dependency and easier to predict the value of one variable on another variable. Value depending easier to measure than reliability.

Reliability dependence is no less important than its quantity. This property is due to the representativeness of the study sample. Reliability depending describes how likely it is that this dependence will again be found in other data.

With the growth of the value of the dependent variable reliability usually increases.