Структурное (комбинаторное) определение количества информации (по Хартли).

Данное определение количества информации применимо лишь к дискретным сообщениям, причем таким, у которых символы равновероятны и взаимно независимы. Количество информации, содержащееся в такого рода сообщениях определяют из следующих соображений.

Пусть дан источник дискретных сообщений 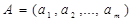, объем алфавита которого равен m. Предположим, что каждое сообщение включает в себя n символов, при этом сообщения различаются либо набором символов, либо их размещением. Число различных сообщений 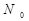, состоящих из n символов, будет 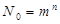. Предположим, что все сообщения равновероятны и одинакова ценность этих сообщений.

Тогда легко подсчитать количество информации, которое несет каждое сообщение.

Вероятность появления каждого такого сообщения 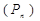может быть легко найдена:

.

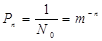И, следовательно, количество информации в одном сообщении 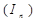, в соответствии с (1.4), равно:

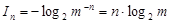(бит). (1.5)

Эту формулу предложил Р.Хартли в 1928 г., и она носит его имя. Разделив 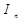на количество символов в сообщении (n), получим значение среднего количества информации 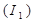, приходящееся на один символ сообщения:

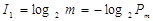(бит / символ), (1.6)

где 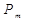- вероятность появления одного символа сообщения.

Из соотношений (1.5) и (1.6) вытекают важные свойства дискретных сообщений, символы которых равновероятны и взаимно независимы.

1. Количество информации в сообщении пропорционально полному числу символов в нем – n и логарифму объема алфавита- m.

2. Среднее количество информации, приходящееся на один символ, зависит только от m – объема алфавита.

В реальных дискретных сообщениях символы часто появляются с различными вероятностями и, более того, часто существуют статистическая связь между символами, характеризующаяся условной вероятностью 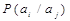, которая равна вероятности появления символа 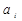после символа 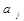. Например, в тексте на русском языке вероятность появления различных символов (букв) различна. В среднем, в тексте из 1000 букв буква О появляется 110 раз, Е – 87, А – 75, Т – 65, Н – 65, С – 55, кроме того, существуют статистические связи между буквами, скажем, после гласных букв не может появиться Ь или Ъ.

Исходя из этого, применение формулы вычисления количества информации по Хартли (1.5) и (1.6) не всегда корректно.