Свойства дисперсии.

1) Дисперсия постоянной величины равна нулю: D(С) = 0

2) Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат: D(СХ) = С² · D(Х)

3) Дисперсия суммы (разности) независимых случайных величин равна сумме дисперсий слагаемых: D(Х₁ ± Х₂ ± ... ± Х_n) = D(Х₁) + D(Х₂) + ... + D(Х_n)

Среднее квадратическое отклонение дискретной случайной величины, оно же стандартное отклонение или среднее квадратичное отклонение есть корень квадратный из дисперсии: σ(X) = √D(X)

5. Таблица случайных величин. Частота появления значения случайной величины.

6. Гистограмма. Полигон распределения.

Для наглядности представления вариационного ряда большое значение имеют его графические изображения. Графически вариационный ряд может быть изображён в виде полигона, гистограммы.

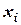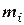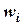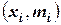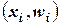Полигон распределения (дословно – многоугольник распределения) называют ломанную, которая строится в прямоугольной системе координат. Величина признака откладывается на оси абсцисс, соответствующие частоты (или относительные частоты ) – по оси ординат. Точки (или ) соединяют отрезками прямых и получают полигон распределения. Чаще всего полигоны применяются для изображения дискретных вариационных рядов, но их можно применять также и для интервальных рядов. В этом случае на оси абсцисс откладываются точки, соответствующие серединам данных интервалов.

Гистограммой распределения называют ступенчатую фигуру[26], состоящую из прямоугольников, основанием которых служат частичные интервалы длиною 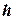, а высоты пропорциональны частотам (или относительным частотам) и равны 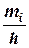– плотность частоты (или 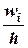– плотность относительной частоты). Для построения гистограммы на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстояни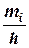и (или 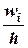). Заметим, что площадь гистограммы частот (относительных частот) равна сумме всех частот (относительных частот), то есть, равна объему выборки (то есть – единице).

7. Медиана и мода.

Модой 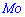дискретной случайной величины 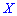называют те ее возможное значение, которые соответствует наибольшей вероятности появления (т.е. такое значение величины 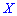, которое случается чаще всего при проведении экспериментов, опытов, наблюдений). В случае случайной величины модой называют то ее возможное значение, которому соответствует максимальное значение плотности вероятностей

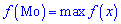
В зависимости от вида функции 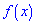случайная величина 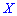может иметь разное количество мод. Если случайная величина имеет одну моду, то такое распределение вероятностей называют одномодальным; если распределение имеет две моды — двухмодальным и более – мультимодальным.

Существуют и такие распределения, которые не имеют моды, их называют антимодальными. Медианой случайной величины 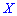называют то ее значения, для которого выполняются равенство вероятностей событий, то есть, плотность вероятностей справа и слева одинаковы и равны половине (0,5)

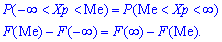
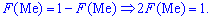
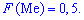
Графически мода и медиана изображенные на рисунке

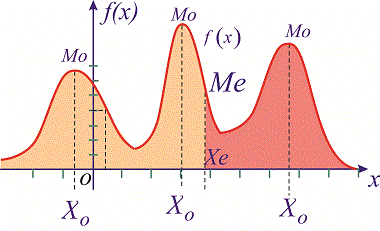
При таком значению случайной величины график функции распределения делится на части с одинаковой площадью. Непрерывная случайная величина имеет только одно значение медианы. Для дискретной случайной величины медиану обычно не определяют, однако в некоторой литературе приводятся правила, согласно которым, для ряда случайных величин размещенных в порядке возрастания (вариационного ряда) моду определяют распределения: если есть нечетное количество случайных величин 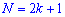то медиана равна средней величине

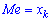
в случае четного количества 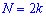полусумме средних величин

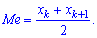
8. Среднее значение.

Средней арифметической величиной называется такое среднее значение признака, при вычислении которого общий объем признака (сумма значений признака) в изучаемой совокупности сохраняется неизменным. Иначе можно сказать, что средняя арифметическая величина – это среднее слагаемое, то есть при ее вычислении общий объем (сумма всех значений) признака мысленно распределяется поровну между всеми единицами совокупности. Исходя из определения, формула средней арифметической величины имеет вид

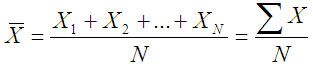
По этой формуле вычисляются средние величины первичных признаков, если известны индивидуальные (отдельные) значения признака. Если изучаемая совокупность велика, то исходная информация чаще представляет собой ряд распределения или группировку, как, например, следующая таблица, где приведен условный пример дискретного ряда распределения студентов по возрасту:

Средний возраст должен представлять собой результат равномерного распределения общего (суммарного) возраста всех студентов. Общий (суммарный) возраст всех студентов, согласно исходной информации в вышеприведенной таблице, можно получить как сумму произведений значений признака в каждой группе Xi, на число студентов с таким возрастом fi (частоты). Получим формулу:

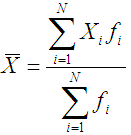
Такую форму средней арифметической величины называют взвешенной арифметической средней. В качестве весов здесь выступают количество единиц совокупности (fi) в разных группах. Название «вес» выражает тот факт, что разные значения признака имеют неодинаковую «важность» при расчете средней величины. «Важнее», весомее возраст студентов 18, 19, 20 лет, а такие значения возраста как 17, 20 или 21 при расчете средней не играют большой роли – их «вес» мал. По формуле средней арифметической взвешенной по данным в условном примере получим:

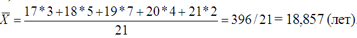
Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменную сумму квадратов исходных величин, то средняя будет являться квадратической средней величиной. Ее формула следующая:

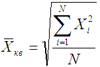
Аналогично, если по условиям задачи необходимо сохранить неизменной сумму кубов индивидуальных значений признака при их замене на среднюю величину, мы приходим к средней кубической величине, имеющей вид:

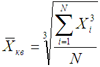
Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменным произведение индивидуальных величин, то следует применить геометрическую среднюю величину, имеющую следующий вид:

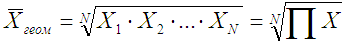
9. Равномерное распределение.

Определение. Непрерывная случайная величина Х имеет равномерное распределение на отрезке [а, в], если на этом отрезке плотность распределения вероятности случайной величины постоянна, т. е. если дифференциальная функция распределения f(х) имеет следующий вид:

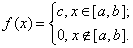
Иногда это распределение называют законом равномерной плотности. Про величину, которая имеет равномерное распределение на некотором отрезке, будем говорить, что она распределена равномерно на этом отрезке.

Найдем значение постоянной с. Так как площадь, ограниченная кривой распределения и осью Ох, равна 1, то

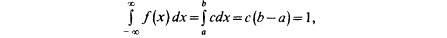
откуда с=1/(b-a).

Теперь функцию f(x) можно представить в виде

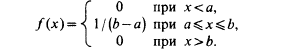
Построим функцию распределения F(x), для чего найдем выражение F(x) на интервале [a, b]:

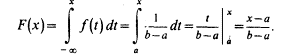
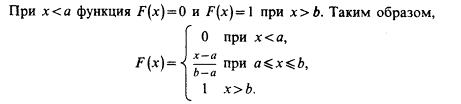
Графики функций f(x) и F(x) имеют вид:

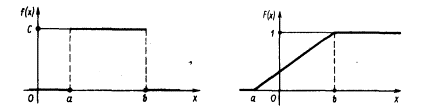
Найдем числовые характеристики.

Используя формулу для вычисления математического ожидания НСВ, имеем:

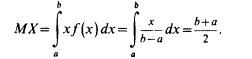
Таким образом, математическое ожидание случайной вели­чины, равномерно распределенной на отрезке [a, b] совпадает с серединой этого отрезка.

Найдем дисперсию равномерно распределенной случайной величины:

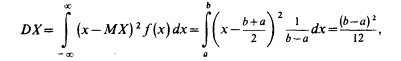
откуда сразу же следует, что среднее квадратическое отклонение:

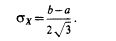
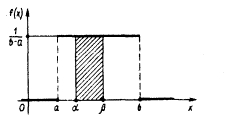
Найдем теперь вероятность попадания значения случайной величины, имеющей равномерное распределение, на интервал (a,b), принадлежащий целиком отрезку [a, b]: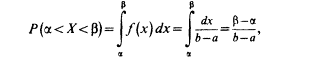

Геометрически эта вероятность представляет собой площадь заштрихованного прямоугольника. Числа а и b называются параметрами распределения и однозначно определяют равномерное распределение.

10. Распределение Бернулли.

Пусть производится 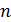независимых испытаний, в каждом из которых событие 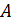может появиться либо не появиться. Вероятность наступления события во всех испытаниях постоянна и равна 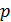(следовательно, вероятность непоявления 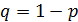)- Рассмотрим в качестве дискретной случайной величины 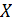число появлений события 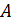в этих испытаниях.

Поставим перед собой задачу: найти закон распределения величины 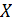. Для ее решения требуется определить возможные значения 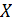и их вероятности. Очевидно, событие 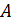в 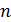испытаниях может либо не появиться, либо появиться 1 раз, либо 2 раза, ..., либо 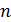раз. Таким образом, возможные значения 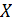таковы: 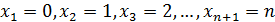. Остается найти вероятности этих возможных значений, для чего достаточно воспользоваться формулой Бернулли:

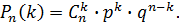
(5.1)

где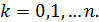

Формула (5.1) и является аналитическим выражением искомого закона распределения.

Биномиальным называют распределение вероятностей, определяемое формулой Бернулли. Закон назван «биномиальным» потому, что правую часть равенства (5.1) можно рассматривать как общий член разложения бинома Ньютона:

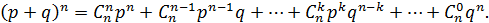
Таким образом, первый член разложения 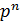определяет вероятность наступления рассматриваемого события 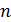раз в 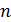независимых испытаниях; второй член 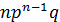определяет вероятность наступления события 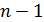раз; ... ; последний член 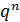определяет вероятность того, что событие не появится ни разу.

Напишем биномиальный закон в виде таблицы:

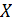
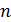
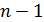
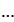
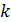
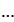
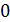
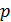
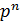
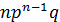
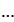
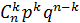
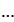
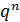
11. Распределение Пуассона.

Пусть производится 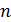независимых испытаний, в каждом из которых вероятность появления события 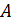равна 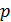. Для определения вероятности 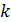появлений события в этих испытаниях используют формулу Бернулли. Если же 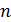велико, то пользуются асимптотической формулой Лапласа. Однако эта формула непригодна, если вероятность события мала ( 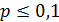). В этих случаях ( 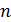велико, 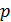мало) прибегают к асимптотической формуле Пуассона.

Итак, поставим перед собой задачу найти вероятность того, что при очень большом числе испытаний, в каждом из которых вероятность события очень мала, событие наступит ровно 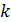раз. Сделаем важное допущение: произведение 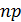сохраняет постоянное значение, а именно 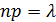. Как будет следовать из дальнейшего, это означает, что среднее число появлений события в различных сериях испытаний, т.е. при различных значениях 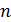, остается неизменным.

Воспользуемся формулой Бернулли для вычисления интересующей нас вероятности:

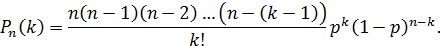
Так как 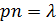, то 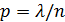. Следовательно,

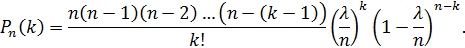
Приняв во внимание, что 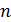имеет очень большое значение, вместо 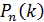найдем 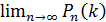. При этом будет найдено лишь приближенное значение отыскиваемой вероятности: 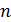хотя и велико, но конечно, а при отыскании предела мы устремим 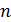к бесконечности. Заметим, что поскольку произведение 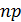сохраняет постоянное значение, то при 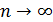вероятность .

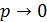Итак,

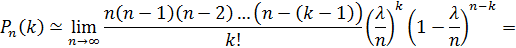
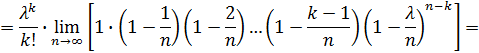
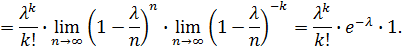
Таким образом (для простоты записи знак приближенного равенства опущен),

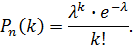
Эта формула выражает закон распределения Пуассона вероятностей массовых ( 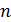велико) и редких ( 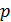мало) событий.

12. Нормальный закон распределения.

Нормальный закон распределения играет в теории вероятностей особую роль. Он является наиболее часто встречающимся на практике законом распределения вероятностей. Нормальному распределению приближенно подчиняется сумма достаточно большого числа независимых случайных величин, описываемых какими угодно законами распределения. Приближение выполняется тем точнее, чем большее количество случайных величин суммируется. А большинство встречающихся на практике величин, таких, например, как ошибки измерений, ошибки стрельбы, могут быть представлены как суммы большого числа малых слагаемых – элементарных ошибок, каждая из которых вызвана отдельной независимой причиной. Особенности отдельных законов распределения нивелируются в общей сумме и эта сумма оказывается подчинена закону, близкому к нормальному. Главное, чтобы элементарные ошибки играли в общей сумме сравнительно малую роль.

Центральная предельная теорема. Если случайная величина Х представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то Х имеет распределение, близкое к нормальному.

Дадим определение нормального распределения случайной величины.

Говорят, что случайная величина Х распределена по нормальному закону с параметрами а и 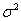, если плотность распределения вероятностей имеет вид:

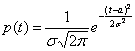, –¥<t<¥.

Вероятностный смысл параметров а и 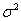таков: а – математическое ожидание случайной величины Х, s – среднее квадратическое отклонение величины.

Иногда такой закон распределения называют Гауссовским. График плотности нормального распределения называют нормальной кривой (кривой Гаусса). На рис. 6.11 изображены нормальные кривые с параметрами а=1 и , , .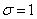

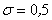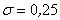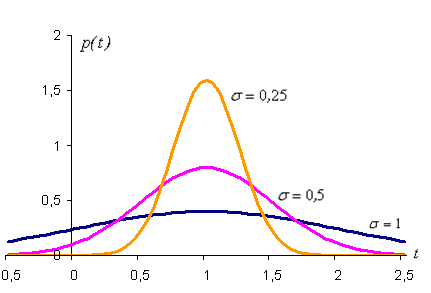
Рис. 6.11

Из рис. 6.11 видно, что положение пика кривых определяется параметром а=1, а параметр s (среднее квадратическое отклонение) характеризует форму нормальной кривой. При увеличении s уменьшается максимум кривой распределения, сама кривая становится более пологой, растягиваясь вдоль оси абсцисс. И, наоборот, при уменьшении s возрастает максимум кривой распределения, сама кривая становится более «островершинной». Площадь, ограниченная любой нормальной кривой и осью абсцисс, равна единице. Параметр а (математическое ожидание величины) определяет положение максимума на оси абсцисс, не влияя на форму кривой. На рис. 6.12 показаны нормальные кривые с одинаковым средним квадратическим отклонением 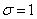и разными математическими ожиданиями а=–1, а=0, а=1.

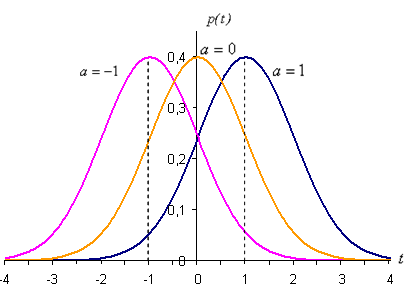
Рис. 6.12

Нормальное распределение с параметрами а=0 и 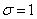называется нормированным. Плотность нормированного распределения

.

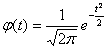Значения этой функции на отрезке [0:3] с шагом 0,01 приведены в таблице

13. Распределение .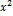

Распределение Пирсона 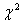(хи - квадрат) – распределение случайной величины

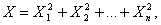
где случайные величины X₁, X₂,…, X_n независимы и имеют одно и тоже распределение N(0,1). При этом число слагаемых, т.е. n, называется «числом степеней свободы» распределения хи – квадрат.

Распределение хи-квадрат используют при оценивании дисперсии (с помощью доверительного интервала), при проверке гипотез согласия, однородности, независимости, прежде всего для качественных (категоризованных) переменных, принимающих конечное число значений, и во многих других задачах статистического анализа данных.

14. Объем генеральной совокупности и выборки.

Основу статистического исследования составляет множество данных, полученных в результате измерения одного или нескольких признаков. Реально наблюдаемая совокупность объектов, статистически представленная рядом наблюдений 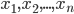случайной величины 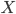, является выборкой, а гипотетически существующая (домысливаемая) — генеральной совокупностью. Генеральная совокупность может быть конечной (число наблюдений N = const) или бесконечной (N = ∞), а выборка из генеральной совокупности — это всегда результат ограниченного ряда 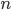наблюдений. Число наблюдений 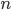, образующих выборку, называется объемом выборки. Если объем выборки 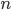достаточно велик (n → ∞) выборка считается большой, в противном случае она называется выборкой ограниченного объема. Выборка считается малой, если при измерении одномерной случайной величины 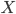объем выборки не превышает 30 (n <= 30), а при измерении одновременно нескольких (k) признаков в многомерном пространстве отношение nкkне превышает10 (n/k < 10). Выборка образует вариационный ряд, если ее члены являются порядковыми статистиками, т. е. выборочные значения случайной величины Х упорядочены по возрастанию (ранжированы), значения же признака называются вариантами.

Пример. Практически одна и та же случайно отобранная совокупность объектов — коммерческих банков одного административного округа Москвы, может рассматриваться как выборка из генеральной совокупности всех коммерческих банков этого округа, и как выборка из генеральной совокупности всех коммерческих банков Москвы, а также как выборка из коммерческих банков страны и т.д.

15. Случайный выбор. Репрезентативность.

Основные понятия выборочного метода:

- Генеральная совокупность –множество объектов, которые являются предметом исследования, определенным программой исследования, территориальными и временными границами. Всегда есть признак (набор признаков), по значению которого можно однозначно определить, относится данный объект к генеральной совокупности или нет.

- Выборочная совокупность (выборка) –число объектов генеральной совокупности, выступающих в качестве объектов наблюдения.

- Единица отбора – элемент генеральной совокупности, который выступает единицей счета в различных процедурах отбора при формировании выборки.

- Единица наблюдения – элемент выборочной совокупности, который непосредственно подвергается исследованию (наблюдению). Единица наблюдения и единица отбора могут совпадать и не совпадать.

- Репрезентативность выборки –свойство выборки адекватно отражать, моделировать характеристики генеральной совокупности.

К условиям репрезентативности выборки относятся:

- Правильное определение объема выборки;

- Минимизация ошибок выборки;

- Применение адекватных методов отбора (построения выборки).

Рассмотрим процедуру определения объема выборки. Объем выборки определяется тремя факторами:

1. степень однородности изучаемых объектов по значимым для исследования характеристикам;

2. целесообразный уровень надежности выводов исследования;

3. степень дробности группировок анализа, планируемых для решения задач исследования;

Роль первых двух условий очевидна, если рассмотреть формулу для определения объема выборки (1). Здесь степень однородности изучаемых объектов по значимым для исследования характеристикам отражена как дисперсия признака в генеральной совокупности, а целесообразный уровень надежности выводов исследования – как задаваемая исследователем предельная ошибка выборки. Данная формула (для повторного отбора) применяется для больших генеральных совокупностей.

n = σ² / μ² = t² σ² / ∆² (1)

где σ² – дисперсия признака в генеральной совокупности

μ – средняя ошибка выборки

t – коэффициент доверия (критерий Стьюдента), t = ∆ / μ

∆ - предельная ошибка выборки (величина доверительного интервала)

Как правило, σ² не известна. Вместо нее в формулу можно подставить ее оценку s², вычисленную по результатам пилотажного исследования объемом n*<n:

s² = (n* σ²) / (n* - 1)

s² вычисляется по каждому вопросу анкеты и для определения объема выборки берется наибольшая величина.

В реальных исследованиях применяется и формула (2) для бесповторного отбора:

n = t² σ² N / (∆² N + t² σ²) (2)

где N – объем генеральной совокупности.

Необходимо помнить, что исследования проводятся с различными целями, и не всегда требуется особо высокая точность (стандартная 5% ошибка выборки). Чем меньшая точность необходима (то есть чем больше допустимая ошибка выборки), тем меньшим может быть объем выборки (и соответственно, дешевле исследование). В практической работе можно пользоваться эмпирическими таблицами, которые отражают зависимость между объемом генеральной совокупности, объемом выборки и предельной ошибкой выборки

16. Идея выборочного распределения.

Рассмотрим реализацию выборки на одном элементарном исходе 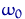— набор чисел 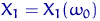, , 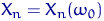. На подходящем вероятностном пространстве введем случайную величину 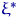, принимающую значения 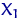, , 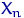с вероятностями по 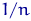(если какие-то из значений совпали, сложим вероятности соответствующее число раз). Таблица распределения вероятностей и функция распределения случайной величины 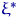выглядят так:

Распределение величины 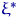называют эмпирическим или выборочным распределением. Вычислим математическое ожидание и дисперсию величины 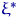и введем обозначения для этих величин:

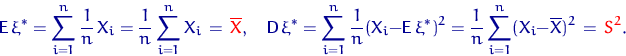
Точно так же вычислим и момент порядка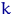

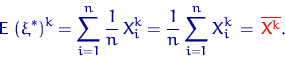
В общем случае обозначим через 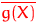величину

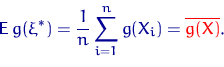
Если при построении всех введенных нами характеристик считать выборку 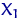, , 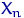набором случайных величин, то и сами эти характеристики — 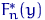, , , , 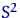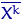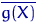— станут величинами случайными. Эти характеристики выборочного распределения используют для оценки (приближения) соответствующих неизвестных характеристик истинного распределения.

Причина использования характеристик распределения 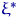для оценки характеристик истинного распределения 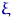(или 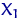) — в близости этих распределений при больших .

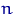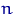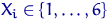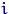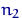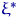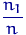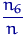Рассмотрим, для примера, подбрасываний правильного кубика. Пусть — количество очков, выпавших при -м броске, . Предположим, что единица в выборке встретится раз, двойка — раз и т.д. Тогда случайная величина будет принимать значения 1, , 6 с вероятностями , , соответственно. Но эти пропорции с ростом 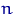приближаются к 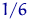согласно закону больших чисел. То есть распределение величины 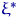в некотором смысле сближается с истинным распределением числа очков, выпадающих при подбрасывании правильного кубика.

17. Статистическое распределение выборки.

Статистическим распределением выборки или вариационным рядом называется перечень вариант (в возрастающем порядке) и соответствующих им частот (относительных частот). При этом вариантаминазываютсявсевозможные значения 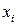генеральной совокупности.

Например, пусть рассматривается выборка, причем: признак Х₁ встречается n₁ раз; признак Х₂ встречается n₂ раз; …; признак Х_k встречается n_k раз.

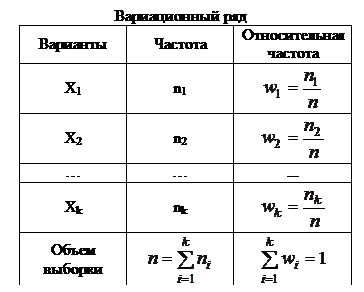
Если количество вариантов 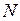слишком велико или близко к объему выборки, то целесообразно составить вариационный ряд по группированным данным.

18. Виды статистических оценок.

Пусть требуется изучить некоторый количественный признак генеральной совокупности. Допустим, что из теоретических соображений удалось установить, какое именно распределение имеет признак и необходимо оценить параметры, которыми оно определяется. Например, если изучаемый признак распределен в генеральной совокупности нормально, то нужно оценить математическое ожидание и среднее квадратическое отклонение; если признак имеет распределение Пуассона – то необходимо оценить параметр l.

Обычно имеются лишь данные выборки, например значения количественного признака 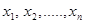, полученные в результате n независимых наблюдений. Рассматривая 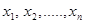как независимые случайные величины 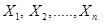можно сказать, что найти статистическую оценку неизвестного параметра теоретического распределения – это значит найти функцию от наблюдаемых случайных величин, которая дает приближенное значение оцениваемого параметра. Например, для оценки математического ожидания нормального распределения роль функции выполняет среднее арифметическое:

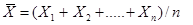
Для того чтобы статистические оценки давали корректные приближения оцениваемых параметров, они должны удовлетворять некоторым требованиям, среди которых важнейшими являются требования несмещенности и состоятельности оценки.

Пусть 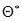– статистическая оценка неизвестного параметра 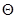теоретического распределения. Пусть по выборке объема n найдена оценка 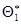. Повторим опыт, т.е. извлечем из генеральной совокупности другую выборку того же объема и по ее данным получим другую оценку 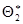. Повторяя опыт многократно, получим различные числа 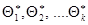. Оценку 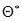можно рассматривать, как случайную величину, а числа 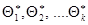– как ее возможные значения.

Если оценка 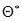дает приближенное значение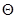
с избытком, т.е. каждое число 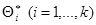больше истинного значения 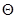то, как следствие, математическое ожидание (среднее значение) случайной величины 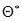больше, чем :

.

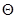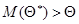Аналогично, если 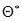дает оценку с недостатком, то .

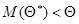Таким образом, использование статистической оценки, математическое ожидание которой не равно оцениваемому параметру, привело бы к систематическим (одного знака) ошибкам. Если, напротив, 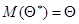, то это гарантирует от систематических ошибок.

Несмещенной называют статистическую оценку 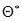, математическое ожидание которой равно оцениваемому параметру 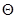при любом объеме выборки .

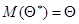Смещенной называют оценку, не удовлетворяющую этому условию.

Несмещенность оценки еще не гарантирует получения хорошего приближения для оцениваемого параметра, так как возможные значения 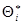могут быть сильно рассеяны вокруг своего среднего значения, т.е. дисперсия 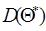может быть значительной. В этом случае найденная по данным одной выборки оценка, например 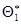, может оказаться значительно удаленной от среднего значения 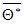, а значит, и от самого оцениваемого параметра.

Эффективной называют статистическую оценку, которая, при заданном объеме выборки n, имеет наименьшую возможную дисперсию.

При рассмотрении выборок большого объема к статистическим оценкам предъявляется требование состоятельности.

Состоятельной называется статистическая оценка, которая при n®¥ стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при n®¥ стремится к нулю, то такая оценка оказывается и состоятельной.

19. Доверительный интервал.

Доверительным называется интервал, который с заданной надежностью 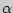покрывает оцениваемый параметр.

Для оценки математического ожидания 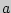случайной величины 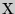, распределенной по нормальному закону, при известном среднем квадратическом отклонении 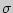служит доверительный интервал

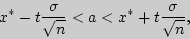
где 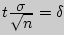- точность оценки, 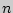- объем выборки, - выборочное среднее, 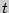- аргумент функции Лапласа, при котором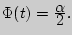

Пример.Найти доверительный интервал для оценки с надежностью 0,9 неизвестного математического ожидания 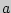нормально распределенного признака 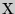генеральной совокупности, если среднее квадратическое отклонение , выборочная средняя и объем выборки .

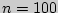Решение. Требуется найти доверительный интервал

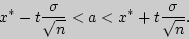
Все величины, кроме 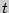, известны. Найдем 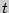из соотношения .

По таблице приложения находим 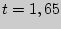и получаем доверительный интервал .

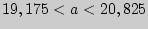Если среднее квадратическое отклонение 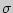неизвестно, то для оценки 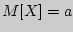служит доверительный интервал

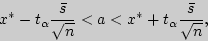
где 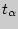находится в приложении 4 по заданным 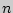и 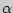, а вместо 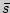часто бывает возможно подставить любую из оценок

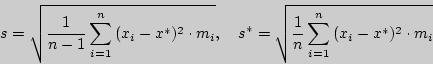
- исправленное среднеквадратическое, статистическое среднеквадратическое отклонения соответственно. При увеличении 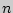обе оценк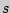и и 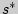будут различаться сколь угодно мало и будут сходиться по вероятностям к одной и той же величине .

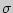20. Доверительная вероятность.

Под доверительным интервалом понимают случайный интервал, который с некоторой вероятностью α накрывает истинное значение искомого параметра:

Вероятность α называют доверительной вероятностью. Она характеризует достоверность (надежность), а доверительный интервал длиной 2γ – точность определения неизвестного значения параметра Q _x с помощью оценки Q *_x.

Поясним смысл доверительного интервала. С этой целью выражение (5.18) перепишем в виде

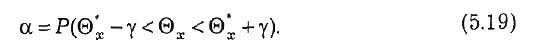
Поскольку оценка Q *_x – величина случайная, то Q *_x – γ θ Q *_x + y также величины случайные, являющиеся границами интервала, который накрывает неизвестное значение оцениваемого параметра Q _x.

Очевидно, что при фиксированной доверительной вероятности а, чем уже доверительный интервал (чем меньше его полуразмах -у), тем точнее будет оценен неизвестный параметр Q _x. Чем больше доверительная вероятность а при фиксированной длине доверительного интервала, тем надежнее будет произведено оценивание параметра Q _x.

Предположим, что для оценивания некоторого параметра Q _x проведено n испытаний, по результатам которых получена точечная оценка Q *_x этого параметра. Затем найдены левая (Q *_x – y) и правая (Q *_x + y) границы интервала. Еще раз проводят n испытаний. По результатам этой серии испытаний вновь находят оценку Q *_x и строят доверительный интервал. Пусть произведено десять таких серий по n испытаний в каждой серии. Соответствующие доверительные интервалы нанесены на горизонтальные линии рис. 5.5.

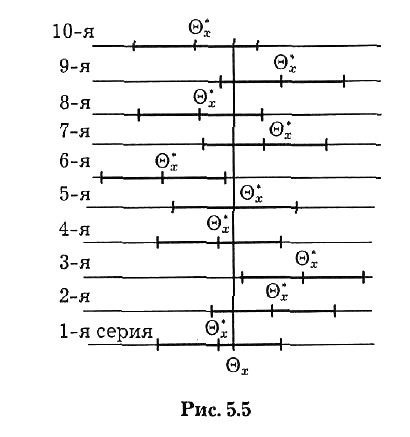
Восемь интервалов из десяти накрыли точку Q _x а интервалы, полученные в 3-й и 6-й сериях, не накрыли Q _x Таким образом, частота события 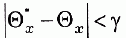равна 0,8. При увеличении числа серий по n испытаний в каждой частота указанного события будет устойчиво колебаться около доверительной вероятности а.

До сих пор рассматривался так называемый симметричный доверительный интервал, т.е. интервал, границы которого равноудалены от полученного значения оценки Q *_x Однако в практике оценивания используют и несимметричные интервалы. У несимметричных интервалов левая граница удалена от значения оценки на величину γ₂, а правая – на γ₁ (γ₁ ≠ γ₂). Длина доверительного интервала равна (γ₁ + γ₂). В этом случае выражение для доверительной вероятности запишем в виде

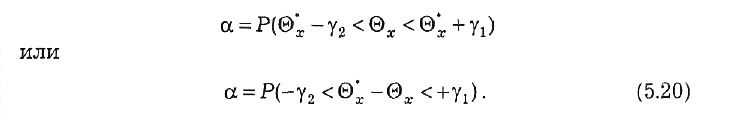
Условию (5.20) при фиксированной вероятности а удовлетворяет бесчисленное множество пар значений γ₁и γ₂.

Предположим, что плотность распределения случайной величины Y = Q *_x – Q _x имеет вид, представленный на рис. 5.6.

На этом же рисунке показаны два интервала, соответствующие одной и той же вероятности

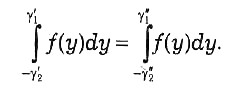
Для устранения указанной неоднозначности используют два способа. Один из них основан на выборе таких значений γ₁и γ₂,при которых обеспечивается симметрия в распределении вероятности (1 – α), т.е. значений, удовлетворяющих условию

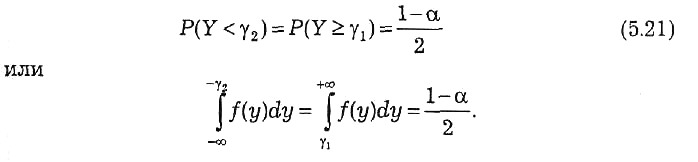
Такие значения γ₂ и γ₁ показаны на рис. 5.7 при несимметричном распределении случайной величины Y.

Доверительный интервал, выбранный таким способом, называют центральным.

21. Зависимые и независимые случайные величины.

Случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какое значение принимает другая случайная величина.

Понятие зависимости случайных величин является очень важным в теории вероятностей.

Условные распределения независимых случайных величин равны их безусловным распределениям.

Определим необходимые и достаточные условия независимости случайных величин.

Теорема. Для того чтобы случайные величины Х и Y были независимы, необходимо и достаточно, чтобы функция распределения системы 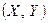была равна произведению функций распределения составляющих.

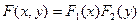
Аналогичную теорему можно сформулировать и для плотности распределения:

Теорема. Для того чтобы случайные величины Х и Y были независимы, необходимо и достаточно, чтобы плотность совместного распределения системы 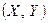была равна произведению плотностей распределения составляющих.

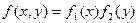
Корреляционным моментом 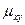случайных величин Х и Y называется математическое ожидание произведения отклонений этих величин.

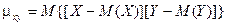
Практически используются формулы:

Для дискретных случайных величин: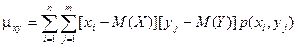

Для непрерывных случайных величин: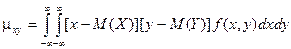

Корреляционный момент служит для того, чтобы охарактеризовать связь между случайными величинами. Если случайные величины независимы, то их корреляционный момент равен нулю.

Корреляционный момент имеет размерность, равную произведению размерностей случайных величин Х и Y. Этот факт является недостатком этой числовой характеристики, т.к. при различных единицах измерения получаются различные корреляционные моменты, что затрудняет сравнение корреляционных моментов различных случайных величин.

Для того, чтобы устранить этот недостаток применятся другая характеристика – коэффициент корреляции.

22. Коэффициент корреляции.

Коэффициентом корреляции 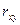случайных величин Х и Y называется отношение корреляционного момента к произведению средних квадратических отклонений этих величин.

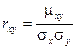
Коэффициент корреляции является безразмерной величиной. Коэффициент корреляции независимых случайных величин равен нулю.

Свойство: Абсолютная величина корреляционного момента двух случайных величин Х и Y не превышает среднего геометрического их дисперсий.

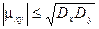
Свойство: Абсолютная величина коэффициента корреляции не превышает единицы.

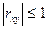
Случайные величины называются коррелированными, если их корреляционный момент отличен от нуля, и некоррелированными, если их корреляционный момент равен нулю.

Если случайные величины независимы, то они и некоррелированы, но из некоррелированности нельзя сделать вывод о их независимости.

Если две величины зависимы, то они могут быть как коррелированными, так и некоррелированными.

Часто по заданной плотности распределения системы случайных величин можно определить зависимость или независимость этих величин.

Наряду с коэффициентом корреляции степень зависимости случайных величин можно охарактеризовать и другой величиной, которая называется коэффициентом ковариации. Коэффициент ковариации определяется формулой:

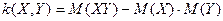
23. Регрессия.

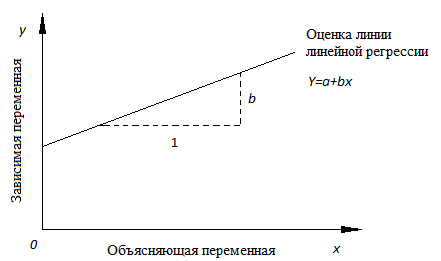
Линия регрессии

Математическое уравнение, которое оценивает линию простой (парной) линейной регрессии:

Y=a+bx.

x называется независимой переменной или предиктором.

Y – зависимая переменная или переменная отклика. Это значение, которое мы ожидаем для y (в среднем), если мы знаем величину x, т.е. это «предсказанное значение y»

· a – свободный член (пересечение) линии оценки; это значение Y, когда x=0 (Рис.1).

· b – угловой коэффициент или градиент оценённой линии; она представляет собой величину, на которую Y увеличивается в среднем, если мы увеличиваем x на одну единицу.

· a и b называют коэффициентами регрессии оценённой линии, хотя этот термин часто используют только для b.

Парную линейную регрессию можно расширить, включив в нее более одной независимой переменной; в этом случае она известна как множественная регрессия.