Решение обыкновенных дифференциальных уравнений.

Постановка задачи. Типы задач для ОДУ.

Известно, что с помощью дифференциальных уравнений можно описать задачи движения системы взаимодействующих материальных точек, химической кинетики, электрических цепей, и др. Конкретная прикладная задача может приводить к дифференциальному уравнению любого порядка, или к системе уравнений любого порядка. Так как любое ОДУ порядка p

u^(p)(x) = f(x, u, u^/, u^//, … u^(p+1)) заменой u^(k)(x) = y_k(x) можно свести к эквивалентной системе из p уравнений первого порядка, представленных в каноническом виде :

y^/_k(x) = y_k+1(x) для 0 ≤ k ≤ p–2 (1)

y^/_p-1(x) = f(x, y₀, y₁, … y_p–1), при этом y₀(x) ≡ u(x). (2)

Покажем такое преобразование на примере уравнения Бесселя: .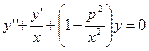

Предполагая тождественную замену y₁(x) ≡ y(x) представим систему ОДУ в следующем виде:

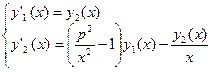
Аналогично произвольную систему дифференциальных уравнений любого порядка можно заменить некоторой эквивалентной системой уравнений первого порядка. Следовательно, алгоритмы численного решения достаточно реализовать для решения системы дифференциальных уравнений первого порядка.

Известно, что система p-го порядка имеет множество решений, которые в общем случае зависят от p параметров {C₁, C₂, … C_p}. Для определения значений этих параметров, т.е. для выделения единственного решения необходимо наложить p дополнительных условий на u_k(x). По способу задания условий различают три вида задач, для которых доказано существование и единственность решения. Это

1) Задача Коши. Задается координата u_k(x₀) = u_k0 начальной точки интегральной кривой в (p+1) – мерном пространстве (k = 1…p). Решение при этом требуется найти на некотором отрезке x₀ ≤ x ≤ x_max .

2) Краевая задача. Это задача отыскания частного решения системы ОДУ на отрезке a ≤ x ≤ b, в которой дополнительные условия налагаются на значения функции u_k(x) более чем в одной точке этого отрезка.

3) Задача на собственные значения. Кроме искомых функций и их производных в уравнение входят дополнительно m неизвестных параметров λ₁, λ₂, … λ_m, которые называются собственными значениями. Для единственности решения на некотором интервале необходимо задать p+m граничных условий.

В большинстве случаев необходимость численного решения систем ОДУ возникает в случае, когда аналитическое решение найти либо невозможно, либо нерационально, а приближенное решение (в виде набора интерполирующих функций) не дает требуемой точности. Численное решение системы ОДУ, в отличие от двух вышеприведенных случаев, никогда не покажет общего решения системы, так как даст только таблицу значений неизвестных функций, удовлетворяющих начальным условиям. По этим значениям можно построить графики данных функций или рассчитать для некоторого x > x₀ соотвествующие u_k(x), что обычно и требуется в физических или инженерных задачах. При этом требуется, чтобы соблюдались условия корректно поставленной задачи.

Метод Эйлера (метод ломаных).

Рассмотрим задачу Коши для уравнения первого порядка:

u^/(x) = f(x, u(x)), x₀ ≤ x ≤ x_max, u(x₀) = u₀. (3)

В окрестности точки x₀ функцию u(x) разложим в ряд Тейлора:

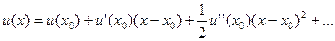(4)

Идея этого и последующих методов основывается на том, что если f(x,u) имеет q непрерывных производных, то в разложении можно удержать члены вплоть до O(h^q+1), при этом стоящие в правой части производные можно найти, дифференцируя (3) требуемое число раз. В случае метода Эйлера ограничимся только двумя членами разложения.

Пусть h – малое приращение аргумента. Тогда (4) превратится в

.

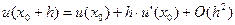Так как в соответствии с (3) u^/(x₀) = f(x₀, u₀), то .

Теперь приближенное решение в точке x₁ = x₀ + h можно вновь рассматривать как начальное условие, т.е. организуется расчет по следующей рекуррентной формуле:

(5),

где y₀ = u₀, а все y_k ­– приближенные значения искомой функции (см. рисунок). В методе Эйлера происходит движение не по интегральной кривой, а по касательной к ней. На каждом шаге касательная находится уже для новой интегральной кривой (что и дало название методу – метод ломаных), таким образом ошибка будет возрастать с отдалением x от x₀.

При 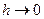приближенное решение сходится к точному равномерно с первым порядком точности. То есть, метод дает весьма низкую точность вычислений: погрешность на элементарном шаге h составляет ½ h² y^//( ½(x_k + x_k+1)), а для всей интегральной кривой порядка h¹. При h = const для оценки апостериорной погрешности может быть применена первая формула Рунге, хотя для работы метода обеспечивать равномерность шага в принципе не требуется.

Метод Эйлера легко обобщается для систем ОДУ. При этом общая схема процесса (5) может быть записана так:

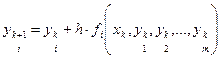(6),

где i = 1…m – число уравнений, k – номер предыдущей вычисленной точки.

Усовершенствованный метод Эйлера-Коши с уточнением.

Данный метод базируется на предыдущем, однако здесь апостериорная погрешность контролируется на каждом шаге вычисления. Как и в предыдущем случае, рассматриваем задачу Коши на сетке с постоянным шагом h. Грубое значение 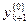вычисляется по формуле (5) и затем итерационным циклом уточняется по формуле

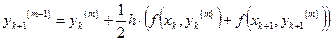, (7)

где m – номер итерации. Итерационный цикл повторяется до тех пор, пока 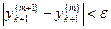. Данная формула также легко обобщается на решение систем ОДУ. Априорная погрешность метода при m = 1 на каждом шаге порядка h³.

Блок-схема метода Эйлера-Коши с уточнением.

Метод Рунге-Кутты II порядка.

Увеличение точности решения ОДУ из предыдущей задачи при заданном шаге h может быть достигнуто учетом большего количества членов разложения функции в ряд Тейлора. Для метода Рунге-Кутты второго порядка следует взять три первых коэффициента, т.е. обеспечить:

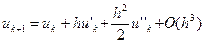. (8)

Переходя к приближенному решению y ≈ u и заменяя производные в (8) конечными разностями, получаем в итоге следующее выражение:

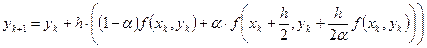, (9)

где 0 ≤ α ≤ 1– свободный параметр. Можно показать, что если f(x,u) непрерывна и ограничена вместе со своими вторыми производными, то решение, полученное по данной схеме, равномерно сходится к точному решению с погрешностью порядка h².

Для параметра α наиболее часто используют следующие значения:

1) α = 1. В этом случае

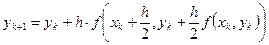. Графически это уточнение можно интерпретировать так: сначала по схеме ломаных делается шаг h/2, и находится значение 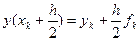. В найденной точке определяется наклон касательной к интегральной кривой, который и будет определять приращение функции для целого шага, т.е. отрезок [AB] (см. рисунок) будет параллелен касательной, проведенной в точке (x_k + h/2, y(x_k + h/2) ) к интегральной кривой.

2) α = ½. В этом случае

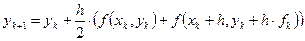. Можно представить, что в этом случае по методу Эйлера сначала вычисляется значение функции и наклон касательной к интегральной кривой в точке x_k+1. Затем находится среднее положение касательной из сравнения соответствующих наклонов в точках x_k и x_k+1, которое и будет использоваться для расчета точки y_k+1.

Метод Рунге-Кутты IV порядка.

Данная схема является наиболее употребительной. Здесь в разложении функции в ряд Тейлора учитываются члены до h⁴ включительно, т.е. погрешность на каждом шаге пропорциональна h⁵. Для практических вычислений используются следующие соотношения, обобщенные в данном случае на решение системы ОДУ:

, где i = 1…p, p – число уравнений в системе.

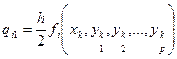; k – номер точки, для которой осуществляется расчет;

;

;

.

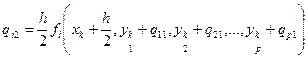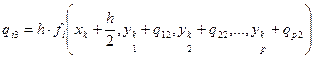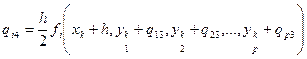К достоинствам метода следует отнести высокую точность вычислений. Схемы более высокого порядка точности практически не употребляются в силу своей громоздкости. Также немаловажно, что метод является явным, т.е. значение y_k+1 вычисляется по ранее найденным значениям за известное заранее число действий.

Все представленные выше схемы допускают расчет с переменным шагом. Например, шаг можно уменьшить там, где функция быстро изменяется, и увеличить в обратном случае. Так, метод Рунге-Кутты-Мерсона позволяет оценивать погрешность на каждом шаге и, в зависимости от полученной оценки принимать решение об изменении шага. Автоматический выбор шага позволяет значительно сократить время вычислений.

Метод Рунге – Кутта - Мерсона.

Этот метод отличается от метода Рунге – Кутта четвертого порядка возможностью оценивать погрешность на каждом шаге и в зависимости от этого принимать решение об изменении шага. Один из вариантов формул:

;

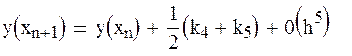
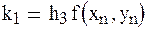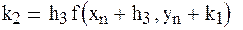
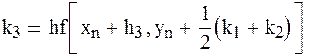
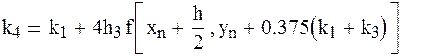
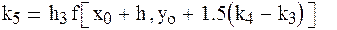
R_n+1 = 0.2k₄ – 0.3k₃ – 0.1k₅ - погрешность на каждом шаге.

Пусть задана максимальна погрешность 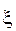. Если 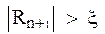, h = h/2 , и n+1 цикл расчета повторяется (с точки x_n, y_n) c новым шагом. Если же

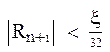, h = 2h

Автоматический выбор шага позволяет значительно сократить время решения ОДУ.

Схема РКМ обобщается на системы ОДУ аналогично классической схеме Рунге – Кутта.

Метод Адамса.

Метод основан на аппроксимации интерполяционными полиномами правых частей ОДУ.

Пусть с помощью любого из методов, рассмотренных выше, вычислено решение заданного дифференциального уравнения в точках x₁, x₂, x₃ (а в точке x₀ решение и так известно – поставлена задача Коши). Полученные значения функции обозначим как y₀, y₁, y₂, y₃, а значения правой части дифференциального уравнения как f₀, f₁, f₂, f₃, где f_k = f(x_k, y_k). Начиная с четвертой точки, на каждом шаге интегрирования дифференциального уравнения вычисления осуществляются по схеме

P(EC)^{m}E

где P – прогноз решения; Е ­– вычисление f(x,y); С – коррекция решения; m ­– количество итераций коррекции. Схемы такого типа называют «прогноз-коррекция»: это подразумевает сначала приблизительное вычисление решение по формуле низкого порядка, а затем уточнение с учетом полученной информации о поведении интегральной кривой.

Прогноз осуществляется по экстраполяционной формуле Адамса:

. (10)

Коррекция осуществляется по интерполяционной формуле Адамса:

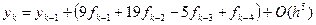. (11)

Вычисление осуществляется по формуле:

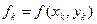
Количество итераций m ≤ p, где p ­– порядок используемого метода. В ходе каждой итерации решается нелинейное уравнение (11) относительно неизвестной y₄ (обычно методом простых итераций).

Иногда в методе Адамса используется схеме PECE на каждом шаге процесса интегрирования, т.е. осуществляется только одна коррекция. В силу сложности вычислений метод используется только в мощных программных пакетах численного анализа. Формулы метода также легко переносятся на решение систем ОДУ первого порядка.

Постановка краевой задачи. Метод стрельбы.

Краевая задача – задача отыскания частного решения системы

(12), 1 ≤ k ≤ p, на отрезке a ≤ x ≤ b, на котором дополнительные условия налагаются на значения функции u_k(x) более чем в одной точке этого отрезка. В качестве примера моно привести задачу нахождения статического прогиба u(x) нагруженной струны с закрепленными концами:

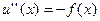, a ≤ x ≤ b, u(a) = u(b) = 0. Здесь f(x) имеет смысл внешней изгибающей нагрузки на единицу длины струны, деленной на упругость струны.

Найти точное решение краевой задачи в элементарных функциях удается редко: для этого надо найти общее решение системы (12) и суметь явно определить из краевых условий значения входящих в него постоянных. Одним из методов, предполагающих численное решение поставленной задачи, является метод стрельбы, в котором краевая задача для системы (12) сводится к задаче Коши для той же системы.

Рассмотрим систему двух дифференциальных уравнений первого порядка

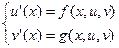(13)

с краевыми условиями

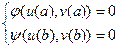(14)

Сначала выберем некоторое значение 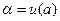, так что 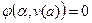. Это уравнение мы можем решить и определить 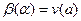. Таким образом у нас появились два числа 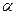и β, которые будут определять задачу Коши 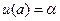, 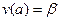для системы (13), удовлетворять левому краевому условию, но не удовлетворять второму уравнению (14). Тем не менее, решим систему ОДУ с задачей Коши каким-либо из известных нам численных методов. Получим решение вида

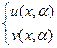(15), зависящее от 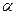как от параметра.

Теперь мы должны каким-либо способом менять параметр 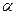до тех пор, пока не подберется такое значение, для которого будет выполнено условие 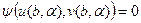(16), т.е. правое краевое условие. Для этого случайным образом берут значения 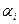до тех пор, пока среди величин 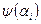не окажется разных по знаку.

Если это осуществилось, пара таких значений определяет интервал 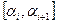, который можно обработать методом дихотомии до получения корня уравнения (16). Нахождение каждого нового значения функции (16) требует нового численного интегрирования для решения ОДУ, что делает этот метод достаточно медленным.

Решение уравнений в частных производных.

К уравнениям в частных производных приводят задачи газодинамики, теплопроводности, переноса излучения, электромагнитных полей, процессов переноса в газах, и др. Независимыми переменными в физических задачах обычно являются время t, координаты 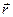, скорости частиц 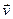. Пример – уравнение теплопроводности

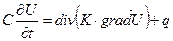, (17)

где U ­– температура, 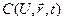– теплоемкость, 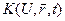– коэффициент теплопроводности, q – плотность источников тепла.

Для решения дифференциальных уравнений в частных производных применяется сеточный метод, суть которого – в разбиении области, в которой ищется решение, сеткой узлов заданной конфигурации, после чего составляется разностная схема уравнения и находится его решение, например методом разностной аппроксимации.

Рассмотрим в качестве примера одномерную задачу, близкую по смыслу к (17):

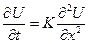. (18)

Здесь 0 ≤ x ≤ a, 0 ≤ t ≤ T.

Граничные условия:

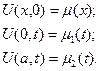
Для одной и той же задачи можно составить много разностных схем. Метод разностной аппроксимации заключается в том, что каждая производная, входящая в дифференциальное уравнение и краевые условия, заменяется разностным выражением, включающим в себя только значения в узлах сетки.

Введем равномерную прямоугольную сетку по x и t с шагом h и τ соответственно и заменить производные соответствующими разностными отношениями. Тогда

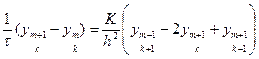. (19)

Здесь 1 ≤ k ≤ N-1 – число точек по координате x; 0 ≤ m ≤ M – число точек по координате t. Число неизвестных в (19) больше числа уравнений, недостающие уравнения выводятся из начальных и граничных условий:

; 0 ≤ k ≤ N.

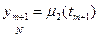; ; 0 ≤ m ≤ M.

Схема (19) содержит в каждом уравнении несколько неизвестных значений функции. Такие схемы называют неявными. Для фактического вычисления решения следует переписать схему так:

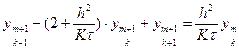, где 1 ≤ k ≤ N-1.

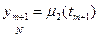; . (20)

Теперь схема представляет собой систему линейных уравнений для определения величин 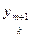; правые части этих уравнений известны, поскольку содержат значения решений для предыдущего индекса времени.

Другим вариантом решения сеточной задачи является использование интегро-интерполяционных методов (методов баланса), в которых дифференциальное уравнение интегрируют по ячейке сетки, приближенно вычисляя интегралы по квадратурным формулам.

Литература

1. Н. Бахвалов, Н. Жидков, Г. Кобельков. Численные методы. М., 2002, 632 с.
2. Н. Калиткин. Численные методы. М., 1972,
3. А. Мудров. Численные методы для ПЭВМ на языках Бейсик, Фортран и Паскаль. Томск, 1992, 270с.
4. А. Самарский. Введение в численные методы. М., , 270с.
5. Ю. Тарасевич. Численные методы на Mathcad’е. Астрахань, 2000, 70с.
6. Г. Коткин, В. Черкасский. Компьютерное моделирование физических процессов с использованием MathLab. Новосибирск, 2001.
7. М. Лапчик, М. Рагулина, Е. Хеннер. Численные методы.М., 2004, 384с.