I книга основных понятий.
1. Точка есть то, что не имеет частей;
2. Линия есть длина без ширины;
3. Границы линии - суть точки;
4. Прямая есть такая линия, одинаково расположена по отношению ко всем своим точкам;
5. Поверхность есть то, что имеет длину и ширину;
6. Границы поверхности - суть линии;
7. Плоскость есть поверхность, которая одинаково расположена по отношению ко всем своим точкам;
ПОСТУЛАТЫ:
1. От всякой точки до всякой другой точки можно провести прямую;
2. Ограниченную прямую можно продлить в неограниченную;
3. Из любого центра можно провести окружность любого радиуса;
4. Все прямые углы равны;
5. (основной) Если две прямые при пересечении с третьей образуют с одной стороны внутренние односторонние углы, сумма которых меньше 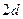 , то эти прямые пересекаются при их достаточном продолжении с этой стороны. (
, то эти прямые пересекаются при их достаточном продолжении с этой стороны. ( 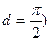
АКСИОМЫ
1. Равные одному и тому же равны между собой ;
2. Если к равным прибавить равные, то получим равные;
3. Если от равных отнимем равные, то получим равные.
4. …….
5. ……
6. ……
7. Совмещающиеся друг с другом равны между собой.
Затем Евклид начинает развивать свою логическую дедуктивную (от общего к частному) систему. Свою геометрию Евклид разделил на две части:
· 1 часть – без использования пятого постулата.
Определение 12.9. Геометрия, построенная на аксиомах Евклида без пятого постулата, называется абсолютной.
В этой геометрической системе содержится конечное число теорем (логических следствий из аксиом и постулатов). В трактовке Евклида их 29.
· 2 часть – добавлен пятый постулат
В этой системе (евклидовой геометрии) количество логических следствий бесконечно.
Недостатки геометрии Евклида: наиболее слабое звено – это определения.
1. Евклид пытается определить исключительно все понятия;
2. Многие определения нечетки, логически неоправданны; ряд определений даётся через неопределенные понятия;
3. Система аксиом неполная. У него нет аксиомы непрерывности (немецкий математик Дедекинд);
4. Постулаты не дают возможности объяснить такие понятии как точка, прямая лежит между двумя её другими точками; две точки плоскости лежат по разным или по одну сторону от прямой;
5. Понятия равенства у Евклида определенно с помощью движения, которые в свою очередь не получило развитие (нет аксиомы движения);
6. Убедительность логики Евклида во многих случаях подкрепляется привычками наших пространственных представлений. А это значит, что «Начала» логически безукоризненного обоснования геометрии не содержат.
На недостатки Евклида указывал уже Архимед (жил на 100-150 лет позднее Евклида). Для того, чтобы сравнивать отрезки, он ввел свою аксиому Архимеда: для любых двух отрезков 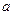 и
и 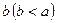 существует
существует 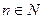 , такое что
, такое что 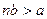 .
.
Дата добавления: 2017-01-29; просмотров: 1959;
