Изменение вариации. Вариационный размах и средние отклонения.

Статистические показатели для характеристики совокупности

Вариационные ряды могут различаться:

1. По тому значению признака, вокруг которого концентрируется большинство вариант.

2. По степени вариации вариант вокруг уровня, по степени отклонения от центральной тенденции ряда.

Соответственно, статистические показатели разделяются на две группы: показатели, характеризующие центральную тенденцию и показатели, измеряющие степень вариации.

К первой группе относятся мода, медиана, средняя арифметическая и средняя геометрическая. Ко второй – вариационный размах, среднее квадратичное отклонение, дисперсия, коэффициенты асимметрии и вариации.

Мода и медиана

Класс, представленный максимальной численностью, называется модальным классом (Мо).

Медиана (Ме) – это значение переменной (варианты), находящееся точно в середине ряда. Чтобы получить медиану, нужно проранжировать переменные от минимального значения к максимальному. При нечетном числе значение варианты – середина вариационного ряда. При четном – необходимо взять 2 значения вариант в середине ряда и разделить на 2.

Медиана и мода имеют в настоящее время ограниченное применение, но если обрабатываются условные единицы (например, в баллах), без них не обойтись.

Средняя арифметическая и ее свойства

Обозначается x c чертой

x_ср= ∑x_i/n

Математические свойства средней арифметической:

1. Если каждую из вариант, для которой вычислялась средняя арифметическая, увеличить или уменьшить на определенную величину, то средняя арифметическая увеличится или уменьшится на эту же величину. (x₁-a), (x₂-a), (x₃-a), то средняя арифметическая для этой совокупности будет равна (x-a).

2. Алгебраическая сумма отклонений отдельных вариант от средней арифметической равняется нулю.

(x₁-x)+ (x₂-x)..+ (x_n-x)=0

3. Суммы квадратов отклонений от средней арифметической меньше суммы квадратов отклонений от любой другой величины А, не равной x_ср.

∑(x_i-x_ср)²<∑(x_i-A)², если А≠x_ср

Взвешенная средняя арифметическая

Если выборка сложная, то можно вычислить взвешенную среднюю арифметическую, которая вычисляется по формуле:

x_ср=(x₁n₁+x₂n₂+x₃n₃…+x_kn_k)/(n₁+n₂+n₃…+n_k),

где x_1, x_2, x₃ – средние арифметические отдельных совокупностей, n1, n2, n3 – число членов в каждой совокупности.

Изменение вариации. Вариационный размах и средние отклонения.

Для характеристики совокупности необходимо вычислить не только среднюю арифметическую, но и величину вариационного размаха. Пример – число щенков в помете 5 норок в 3 выборках:

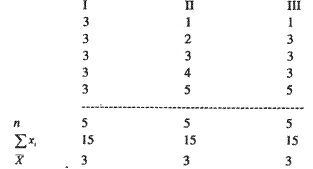
Как видно, несмотря на одинаковые средние арифметические, величина вариационного размаха в 3 выборках сильно различается. В данном случае лучше сравнивать варианты друг с другом или какой-то постоянной величиной, которой может служить x_ср.

Поэтому, чтобы охарактеризовать величину вариационного размаха, используют такие показатели, как дисперсия и среднеквадратическое (стандартное) отклонение.

Дисперсия – это сумма квадратов отклонения переменных от средней

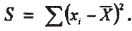
Но в данном случае дисперсия накапливается (увеличивается) с ростом числа значений. Поэтому необходимо ее осреднить:

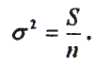
Среднее квадратическое отклонение – это корень квадратный из дисперсии. Оно находится по формуле:

σ = (∑(x_i-x_ср)²/(n-1))^1/2

где σ - стандартное (среднеквадратическое) отклонение.

Степени свободы:

Величина n-1 получила название число степеней свободы. Ее обозначают двумя латинскими буквами df (degree of freedom).