И сопротивлением грунта сдвигу

Зависимость между нормальным давлением

На практике значения показателей сопротивления грунта сдвигу используются для расчетов прочности и устойчивости грунтов.

Деформации сдвига – это смещение одной части грунта по другой, вызванное действием касательных напряжений от внешней нагрузки. Под действием сдвигающих усилий отдельные зерна грунта перемещаются и структура грунта в зоне сдвига нарушается. Грунт оказывает при этом сопротивление сдвигающим усилиям: для сыпучих грунтов это сопротивление внутреннего трения, а для связанных грунтов, кроме того, сопротивление сил сцепления. Сцепление в грунте, как было указано ранее, может быть капиллярным, молекулярным и структурным.

Сопротивление грунтов сдвигу изучают экспериментально в условиях предельного напряженного состояния.

Предельным напряженным состоянием грунта называют такое состояние, при котором малейшее увеличение внешнего воздействия вызывает нарушение равновесия; при этом сопротивление сдвигу равно предельному для данного грунта значению.

Следовательно, сдвиг представляет собой пластическую деформацию – незатухающее скольжение одной части грунта по другой, соответствующее преодолению предельно-напряженного состояния.

Сопротивление грунтов сдвигу определяют в лаборатории чаще всего по срезу грунта в срезных приборах по заранее фиксированным плоскостям или по сдвигу грунта по плоскостям максимальных тангенциальных напряжений при раздавливании.

Первый метод получил наибольшее распространение в практике.

Схема срезного прибора изображена на рис.2.19. Он представляет собой обойму из двух металлических колец, между которыми оставлен небольшой зазор (около 0,5 мм). Одно кольцо укреплено неподвижно, другое кольцо может смещаться горизонтально. Обжатие грунта, помещенного в обойму, производится аналогично обжатию при компрессионных испытаниях. После стабилизации осадки к подвижной обойме прибора прикладывают небольшими ступенями горизонтальное усилие до наступления незатухающей деформации сдвига по зазору между кольцами прибора.

Испытания проводят на нескольких (3 - 5) образцах грунта с целью получения ряда экспериментальных точек для построения графической зависимости между величиной давления, нормального к поверхности сдвига, и сопротивлением грунта сдвигу.

Рис.2.19. Схема срезного прибора:

1 – образец грунта;

2 – индикаторы;

3 – пористые штампы;

4 – неподвижная обойма;

5 – шарики;

6 – подвижная обойма

Обжимающее давление P (в Па) определяют как частное от деления полного нормального давления P на площадь образца F, а сдвигающее напряжение t (в Па) – как частное от деления сдвигающей силы Q на площадь среза F.

Для сыпучих грунтов график, построенный по результатам нескольких опытов, представлен на рис.2.20.

Рис.2.20. Зависимость между нормальным давлением и сопротивлением грунта сдвигу для сыпучих грунтов

Зависимость между P и t выражена прямой линией, выходящей из начала координат. Угловой коэффициент прямой представляет собой тангенс угла внутреннего трения j между частицами грунта, а сама зависимость имеет вид

t = tgj×P, (2.36)

где tgj представляет собой коэффициент внутреннего трения, tgj = f. Данная зависимость представляет собой закон Кулона (1773 г.) для сыпучих тел, который гласит: сопротивление сыпучих тел сдвигу есть сопротивление внутреннего трения, прямо пропорциональное нормальному давлению.

Для связных грунтов график более сложный. Экспериментальные точки образуют криволинейную зависимость с максимальной крутизной (кривизной) при малых величинах давлений. Опыты показывают, что при давлении P более 0,05…0,1 МПа криволинейность графика сдвига становится незначительной, поэтому для практических целей можно заменить кривую прямой, которая при этом не проходит через начало координат, а отсекает от оси ординат отрезок c₀. Величина c₀ представляет собой сопротивление связного грунта сдвигу при нормальном давлении P=0, т.е. характеризует собой сцепление частиц (рис.2.21).

Рис.2.21. Зависимость между нормальным давлением и сопротивлением грунта сдвигу для связных грунтов

Уравнение прямой, построенной по экспериментальным точкам, можно записать в следующем виде:

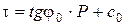. (2.37)

Это уравнение представляет собой математическое выражение закона Кулона для связных тел, который может быть сформулирован так: сопротивление связных грунтов сдвигу есть функция первой степени от нормального давления, состоящая из двух слагаемых – сопротивления внутреннего трения, прямо пропорционального нормальному давлению, и сопротивления сил сцепления, не зависящего от нормального давления.

Таким образом, в законе Кулона предполагается, что коэффициент внутреннего трения f и сила сцепления c₀ – величины постоянные. Однако, учитывая, что внешняя нагрузка уплотняет грунт, способствуя сближению частиц грунта, увеличению числа контактов между ними, следует считать очевидным, что с увеличением внешнего давления сила сцепления грунта должна возрастать. Соответственно, угол j₀ на графике будет представлять собой завышенное значение угла внутреннего трения, т.к. фактически в величину угла наклона прямой к горизонту входит и некоторая доля возрастающих сил сцепления.

Характеристики сопротивления грунта сдвигу имеют большое значение для расчетной практики, поэтому методика раздельного определения сил трения и сил сцепления представляет практический интерес.

Методом, предложенным в свое время ВНИИГом (Всесоюзный научно-исследовательский институт гидротехники), испытывают две серии образцов грунта неизменной плотности. При этом образцы 1-й серии уплотняют тем нормальным давлением, при котором осуществляют сдвиг, а образцы 2-й серии уплотняют максимальным для данного опыта давлением, после чего производят сдвиг при снятии нагрузки до различных для каждого образца ступеней. Условно считают, что срезы образцов 2-й серии осуществляют при неизменной плотности грунта, соответствующей уплотнению образца максимальным для данного опыта давлением. Такое предположение основано на особенностях поведения грунта при разгрузке. Как было показано выше, обратная ветвь компрессионной кривой имеет (при разгрузке до 0,5 - 1 кг/см²) весьма малый наклон к оси давлений, что указывает на незначительные изменения плотности грунта.

По результатам испытаний грунта на сдвиг строим график и в результате получаем прямолинейную зависимость для грунта данной плотности, вполне отвечающую закону Кулона для связных тел (рис. 2.22). На графике испытаний образцов грунта без предварительного уплотнения (прямая 1) на оси ординат отсечен отрезок, выражающий силу сцепления неуплотненного грунта, а на графике грунта, предварительно уплотненного (прямая 2), на оси ординат получаем величину c_max – сила сцепления максимально уплотненного для данного опыта грунта. Полагая, что силы сцепления грунта меняются в зависимости от давления по линейному закону, находим путем линейной интерполяции переменные значения сил сцепления c₁, c₂, c₃, соответствующие нормальным давлениям P₁, P₂, P₃, P₄. При этом угол j, меньшей по величине угла j₀, представляет собой угол внутреннего трения (рис.2.22).

Рис.2.22. Зависимость переменных сил сцепления от величины уплотняющих давлений (метод ВНИИГа):

1 – результаты испытаний без предварительного уплотнения;

2 – то же, с предварительным уплотнением P_max

Методика ВНИИГа исходит из предположения о постоянстве угла внутреннего трения при различных плотностях грунта, в то время как в действительности при уплотнении грунта происходит сближение частиц, увеличение числа контактов и величина угла трения может несколько возрастать. Этим обстоятельством можно пренебречь, поскольку составляющая сил внутреннего трения в общем сопротивлении связных грунтов сдвигу имеет сравнительно малую долю.

Математически уравнение сдвига можно записать так:

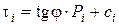, (2.38)

где c_i – сила сцепления, соответствующая данной плотности грунта.

Формулировка закона сопротивления сдвигу связных грунтов может быть следующей: сопротивление связных грунтов сдвигу есть функция первой степени от нормального давления, состоящая из двух слагаемых – сопротивления внутреннего трения и сопротивления сил сцепления; оба слагаемых увеличиваются пропорционально увеличению нормального давления.

2.6.1. Сопротивление сдвигу неконсолидированных грунтов

Выше мы рассмотрели сопротивление грунта сдвигу для случая уплотнения от внешней нагрузки в условиях открытой системы (консолидированно-дренированной).

Важно также рассмотреть сопротивление глинистых грунтов сдвигу по закрытой системе (неконсолидированно-недренированные) и в случае, когда грунт от данной нагрузки еще не уплотнился полностью, то есть еще имеется поровое давление.

На рис.2.23 приведены результаты испытания глинистых грунтов на сдвиг в условиях закрытой системы.

Рис.2.23. Кривые предельных сопротивлений сдвигу связных глинистых грунтов в условиях закрытой системы (неконсолидированно-недренированных): а) зависимость сопротивления сдвигу от влажности; б) кривые сдвига при быстром срезе

Для неконсолидированного состояния полностью водонасыщенных связных грунтов, когда полного уплотнения от данной нагрузки еще не достигнуто, часть сопротивления сдвигу грунта, зависящая от величины нормального давления, будет меньше, так как на скелет грунта передается лишь эффективное давление 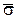, равное разности между полным давлением s и нейтральным u. В данном случае значение сопротивления сдвигу полностью водонасыщенного связного грунта при незавершенной консолидации будет промежуточным между сопротивлением сдвигу, соответствующим начальной влажности грунта, и сопротивлением, соответствующим стабилизированному его состоянию:

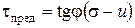(2.39)

или

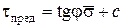, (2.40)

где u – нейтральное (поровое) давление, соответствующее данной степени консолидации; c – эффективное сцепление.

Н.Н.Масловым был предложен метод учета неполной консолидации пылевато-глинистых грунтов, который сводится к испытанию образцов грунта на неконсолидированный сдвиг через различные промежутки времени после приложения давлений одной и той же интенсивности. После сдвига из области среза берут пробы грунта для определения его влажности. По этим данным можно построить график зависимости предельного сопротивления грунта сдвигу от влажности. Серия таких испытаний при различных давлениях P_n дает возможность построить графики кривых предельного сопротивления сдвигу как функции влажности (рис.2.24,а). Пользуясь этими данными, можно построить график зависимости предельного сопротивления сдвигу от давления для любой влажности (рис.2.24,б), а по полученным характеристикам – график зависимости удельного сцепления и угла внутреннего трения от влажности (рис.2.25).

Рис.2.24. Зависимости предельного сопротивления сдвигу грунта

от влажности (а) и от давления (б)

Рис.2.25. Зависимость угла внутреннего трения j и сил сцепления c от влажности w