Розрахунок дерев'яних елементів
Елементами дерев'яних конструкцій є дошки, бруси, бруски, колоди суцільних перерізів з розмірами, зазначеними в сортаментах лісоматеріалів. Вони можуть бути окремими конструкціями, наприклад балками чи стійками, а також бути елементами більш складних конструкцій. У результаті розрахунку розв’язуються слідуючі практичні задачі проектування дерев'яних конструкцій:
Перевірка міцності і прогину елемента полягає у визначенні напружень у перерізах, які не повинні перевищувати розрахункових опорів деревини, а також його прогинів, які не повинні перевершувати граничних, що допускаються нормами.
Підбір перерізів при проектуванні нових дерев'яних конструкцій полягає у визначенні таких розмірів елемента, при яких його міцність і стійкість будуть достатні для сприймання діючих зусиль, а прогини будуть не більше граничних.
Визначення несучої здатністі елемента в процесі обстеження конструкцій під час їхньої експлуатації. Для цього визначають найбільші навантаження і зусилля які може витримувати елемент відомих розмірів, щоб при цьому розрахункові опори деревини і граничні прогини не були перевищені.
Дерев'яні елементи розраховують на розтяг, стиск, згин, розтяг чи стиск із згинном, зминання і сколювання відповідно до норм СНиП 11-25—80 «Нормыпроектирования. Деревянные конструкции». Розрахункові опори, що приводяться нижче, відповідають деревині сосни і ялини. Відповідно до цих же норм проводиться розрахунок дерев'яних елементів, що згинаються, по прогинах.
1. Розтягнуті елементи — це нижні пояси ферм, затяжок арок і деякі стержні інших наскрізних конструкцій. Робота дерев'яних елементів на розтяг є найбільш відповідальню, оскільки вони руйнуються майже миттєво, без помітних попередніх деформації. Тому розтягнуті елементи необхідно виготовляти, як правило, з найбільш міцної деревини 1-го сорту з нормативним опором Rнр = 20 МПа і розрахунковим опором Rp = 10 МПа. Однак при відсутності такого матеріалу допускається в малонапружених елементах застосовувати деревину 2-го сорту з розрахунковим опором Rp =7,0 МПа.
Міцність розтягнутих елементів у тих містях, де вони ослаблені отворами чи врізками, знижується додатково в результаті концентрації напружень у їхніх країв. Це враховується знижуючим коефіцієнтом умов роботи тр = 0,8. При цьому розрахунковий опір деревини 1-го сорту розтягу Rp = 8 МПа.
При наявності ослаблень у межах ділянки довжиною 20 см у різних перерізах поверхня розриву завжди проходить через них. Тому при визначенні ослабленої площі перерізу Ант всі ослаблення на цій довжині сумуються, як би суміщають в одному перерізі (рис. 2.1).
Розрахунок на міцність розтягнутих елементів проводиться на розтягуючу силу N від розрахункових навантажень:

Для підбору перерізів розтягнутих елементів користуються цією ж формулою, написаною для необхідної площі перерізу, враховуючи те, що N і Rp відомо. При цьому Ан = N /Rp. Найбільше розтягуче зусилля, що може витримувати розтягнутий елемент відомих розмірів, можна визначити по цій же формулі, написаній відносно зусилля N == AнтRp. По деформаціях розтягнуті елементи не перевіряються.
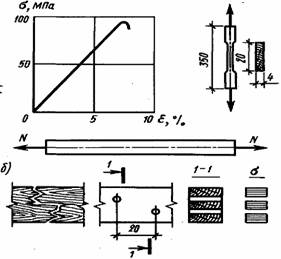
Рис.. 2.1. Розтягнутий елемент: а – графік деформацій і зразок; б- схема роботи і епюра напруженнь.
2. Стиснуті елементи. На стиск працюють стійки, підкоси, верхні пояси й окремі стержні ферм і інших наскрізних конструкцій. Деревина працює на стиск більш надійно, чим на розтяг, але не цілком пружно.
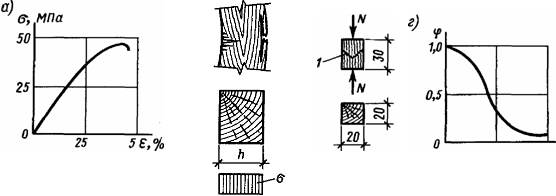
Рис. 2.3. Стиснутий елемент: а — графік деформацій і зразок; б — схеми роботи, руйнування й епюра напруг;
г-графік коефіцієнтів стійкості φ в залежності від гнучкості λ
Вади реальної деревини менше знижують міцність стиснутих елементів, оскільки самі сприймають частину стискаючих напружень. Тому стиснуті елементи рекомендується виготовляти, як правило, з більш доступної деревини 2-го сорту, що має нормативний опір стиску Rнс = 25 МПа і розрахунковий опір стиску Rс = 13 МПа.
Міцність стержня при стиску і втрата його стійкості залежать від площі А і форми його перерізу, довжини l і типу закріплення його кінців, що враховуєтьсякоефіцієнтом стійкості φ, який називають іноді коефіцієнтом поздовжнього згину. Стиснуті дерев'яні елементи розраховуються на міцность і стійкость при дії подовжніх сил стиску N від розрахункових навантажень:

Розрахункова площа перерізу А приймається рівною його повній площі, якщо вона не має ослаблень, або їхня площа не перевищує \/4 площі перерізу . Великі внутрішні ослаблення знижують його несучу здатність, але менше, ніж їхні відносні розміри, і розрахункова площа перерізу приймається при цьому рівною 4/знеослабленої площі перерізу. Симетричні зовнішні ослаблення зменшують міцність елемента прямо пропорційно їхнім розмірам і площа їх виключається. При несиметричних ослабленнях елемент розраховують як позацентрово стиснутий.
Коефіцієнт стійкості елемента φ визначається в залежності від його розрахункової довжини l0 , радіуса інерції перерізу i, гнучкості λ = lo/i і знаходиться з виразів φ = 3000/λ2 при λ>70 і φ= 1—0,8(λ/100)2 при λ<70.
Розрахункова довжина l0 враховує вплив типу закріплення кінців на стійкість стиснутого елемента. При обох шарнірно - закріплених кінцях вона дорівнює геометричній довжині l0 == l. При нижньому защімленому, а верхньому вільному кінці l0 = 2,2l. При нижньому защімленому, а верхньому шарнірному закріпленому кінці l0 == 0,8l , при обох защімлених кінцях l0 = 0,65l.
Радіус інерції перерізу і залежить від площі А и моменту інерції перерізу І, тобто 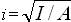 . Радіуси інерції прямокутних переізів з розмірами b и h (де h —менший розмір перерізу) і круглих переізів діаметром d можна приймати рівними 0,29h и 0,25d.
. Радіуси інерції прямокутних переізів з розмірами b и h (де h —менший розмір перерізу) і круглих переізів діаметром d можна приймати рівними 0,29h и 0,25d.
Гнучкість стиснутих елементів обмежується для того, щоб вони не вийшли недостатньо надійними. Основні елементи конструкцій — окремі стійки, пояси й опорні розкоси ферм і ін. — повинні мати гнучкість не більш 120, інші стиснуті елементи основних несучих конструкцій — не більш 150 і стиснуті елементи зв'язків — не більш 200.
Несучу здатність N стиснутого елемента, усі розміри якого і спосіб закріплення кінців відомі, можна визначати по формулі N = φARc. При цьому необхідно попередньо обчислити площу перерізу А, гнучкість λ і коефіцієнт стійкості φ.
Підібрати переріз стиснутого елемента безпосередньо по формулі (2.5) не можна, тому що від його розмірів залежить коефіцієнт стійкості. У цьому випадку можна попередньо приблизно задатися величинами λ і φ. Наприклад, для основних стійок варто приймати гнучкість λ ≈ 80 і φ≈ 0,5, для неосновних елементів гнучкість λ= 120 і φ = 0,2 для елементів зв'язків гнучкість λ = 180 і φ= 0,1. Необхідну площу перерізу Ан можна визначити по формулі Ан = N / Rсφ і потім підібрати розміри перерізу. Гнучкість окремих елементів прямокутного перерізу необхідно визначати найбільшу в напрямку меншого розміру перерізу і меншого радіуса інерції, а при наявності зв'язків визначати гнучкості в напрямку обох осей перерізу і приймати найбільшу.
Відносно короткі елементи, довжина яких не перевищує семикратної висоти перерізу, працюють на стиск без утрати стійкості і розраховуються по формулі

Площа перерізу визначається шляхом виключення з загальної площі площ всіх ослаблень, оскільки вони знижують міцність такого елемента пропорційно їхній величині. Стиснуті елементи, що не мають проміжних закріплень, вигідно приймати квадратного перерізу, однакової стійкості щодо обох осей їхніх перерізів.
3. Елементи які працюють на згинання — балки, дошки настилів,кроквяні ноги, лати — найбільш поширені елементи дерев'яних конструкцій. В таких елементах від навантажень, що діють поперек його подовжньої осі, виникають згинальні моменти М і поперечні сили Q.. Наприклад, в середині прольоту однопрольотної шарнірно обпертої балки від рівномірного навантаження q виникає згинальний момент М = qls/8, а від зосередженої в середині прольоту сили Рзгинальний момент М == Рl /4. Поперечні сили дорівнюють опорним реакціям від цих навантажень.Від дії моменту в перерізах елемента виникають напруження згину σ, що складаються зі стиску у верхній половині перерізу і розтягу в нижній.
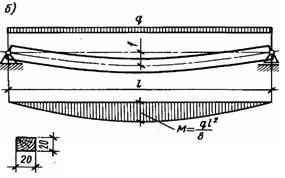
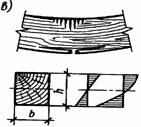
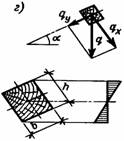
Рис. 2.4. Елементи які працюють на згинання: а — графік прогинів і зразок; б — схема роботи й епюри згинальних моментів; в — схема руйнування й епюри нормальних напружень; г — схема роботи при косому згині й епюра напружень.
Елементи, що згинаються, як і стиснуті, рекомендується виготовляти з деревини 2-го сорту з розрахунковими опорами Rзг = 13 МПа. У брусах з перерізами більшими 13 см Rзг=15 МПа, а в колодах Rзг = 16 МПа.
Розрахунок елементів, що згинаються, по міцності поперечних перерізів проводиться на дію максимальних згинальних моментів М (МН*м) від розрахункових навантажень:

де W — момент опору перерізу (м3).
У найбільш розповсюджених прямокутних перерізах із шириною b и висотою h - W= bh2/6, а для круглих перерізів діаметром d - W=dз/10.
Підбір перерізу елемента, що згинається, по міцності може проводитися також по формулі (2.7). Для цього можна задатися одним з розмірів прямокутного перерізу — b чи h і визначити інший, наприклад:
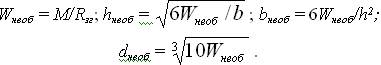
Граничне розрахункове навантаження, що може витримувати елемент, що згинається, по міцності, коли всі його розміри відомі, може бути визначене також за допомогою формули (2.7), переписаної відносно згинаючого моменту М. Наприклад, однопрольотна шарнірно обперта балка прольотом l з розмірами перерізу шириною b и висотою h може витримувати рівномірне навантаження q, визначене в такому порядку:
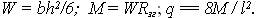
Розрахунок елементів, що згинаються, на сколювання при згині проводиться на дію максимальних поперечних сил Q (МН) від розрахункових навантажень по формулі

де S = bh2/8, м3— статичний момент частини перерізу, що сколюється, відносно його нейтральної осі для прямокутного перерізу
І = bh3/12, м4 — момент інерції всього перерізу;
Rск =-1,6 Мпа - розрахунковий опір сколюванню.
Розрахунок елемента, що згинається, по прогинах полягає у визначенні його найбільшого відносного прогину f/l від нормативних навантажень і перевірці умови, щоб він не переверщував значення, що допускається нормами, що визначається умовою
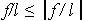
Наприклад, перевірити відносний прогин однопрольотної шарнірно обпертої балки прямокутного перерізу b * h, прольотом l при рівномірному нормативному навантаженні qн (МН/м) можна по формулі
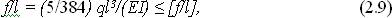
де Е= 104 МПа - модуль пружності.
Якщо відносний прогин балки виходить більший, той переріз повинен бути збільшений і підібраний по прогину. Для цього формулу (2.9) варто переписати відносно необхідного моменту інерції: Інеоб == 5/384/[ЕІ(f/l)]. Після цього можна задатися одним розміром прямокутного перерізу і визначити інший, наприклад, з виразу 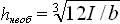 .
.
4. Елементи, які працюють на косе згинання— це лати і прогони похилих покриттів. Косий згин виникає в елементах, осі перерізів яких розташовані похило до напрямку дії навантажень ( рис. 2.4, г).
Вертикальне навантаження, наприклад, рівномірне q, і згинальний момент від нього М при косому згині елемента прямокутного перерізу під кутом α розкладається на нормальні і похилі складові уздовж осей перерізів: qx = q cos α; qу = q sin α; Мх = М cos α; My = М sin α. Відносно цих же осей визначаються моменти опору W і момент інерції І перерізів. Перевірка міцності косозгинальних елементів виконується за формулою

Підбір перерізів елементів може виконуватися методом спроб. При цьому їх варто установлювати великими розмірами прямокутного перерізу в напрямку діїбільших складових діючих навантажень. Розрахунок елементів по прогинах виконується з врахуванням геометричної суми прогинів відносно кожної осі за формулою
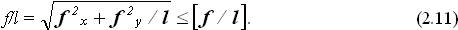
5. Елементи, які працюють на стискання і згинання — це верхні пояси ферм при наявності місцевого, позавузлового навантаження, колони каркасів при позацентровому стиску.
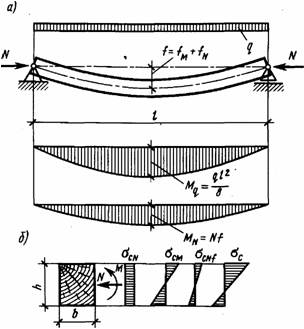
Рис. 2.5.Елементи, що працюють на стискання і згинання: а — схема роботи й епюри згинальних моментів;
б - пюри нормальних напружень.
У перерізі такихелементів діють повздовжні стискаючі сили N, від яких виникають рівномірні напруження стиску і згинальний момент М, від якого виникають стискаючі і розтягуючі напруження, максимальні в крайніх волокнах і нульові на нейтральній осі прямокутного перерізу. Напруження стиску складаються, а напруження стиску і розтягу віднімаються (рис. 2.5). Максимальні стискаючі напруження виникають у крайніх волокнах перерізу в місці дії максимального згинального моменту.
Розрахунок елементів по нормальних напруженнях проводиться на дію максимальних повздовжніх стискаючих сил N і згинальних моментів М від розрахункових навантажень по формулі

де Mд=Mq/ξ— це згинальний момент з врахуванням додаткового згинального моменту, що виникає в результаті прогину елемента f від зовнішнього поперечного навантаження. При цьому стискаючі подовжні сили N починають діяти з ексцентриситетом, рівним f, і виникає додатковий момент МN = Nf. Цей додатковий момент і враховується коефіцієнтом ξ, що залежить від повздовжньої сили N, гнучкості λ, розрахункового опору стиску Rc, площі перерізу А і визначається за формулою
??????
Перевірка на напруження сколювання проводиться з врахуванням коефіцієнта ξ за формулою

Жорсткість елементів перевіряють за формулою

де f0 — прогин від поперечного навантаження.
Елемент, який працює на стискання і згинання повинний бути також перевірений на міцність і стійкість тільки при стиску повздовжньою силою із площини згинання по формулі (2.5). Перевірки стійкості плоскої форми деформування суцільних елементів, як правило, не потрібно.
6. Елементами, які працюють одночасно на розтягання і згинання є нижні пояси ферм, у яких крім розтягу діє ще і згин від міжвузлового навантаження від ваги підвісного перекриття, елементи, розтягуючі сили в яких діють з ексцентриситетом відносно їхніх осей. Схема роботи, епюри згинальних моментів і напружень у перерізах таких елементів показані на рис. 2.6.
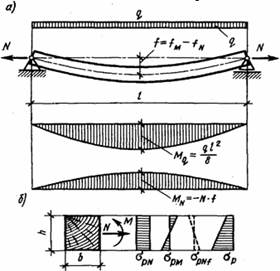
Рис. 2.6.Елементи, які працюють на розтягання та стискання: а — схема роботи й епюри згинальних моментів;б — епюри нормальних напружень.
Міцність елементів перевіряють на дію повздовжніх розтягуючих сил N і згинальних моментів М від діючих розрахункових навантажень по формулі
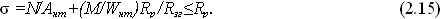
Підбір перерізів розтягнуто-згинальних елементів, можна робити методом спроб, оскільки використовувати для цього формулу 2.15 неможливо. Додаткове рівномірне навантаження, що може витримувати розтягнутий елемент, розтягуючі напруження в перерізах якого значно менші розрахункових, можна визначити з виразу:
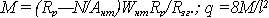
Дата добавления: 2016-12-08; просмотров: 2071;
