Косинус двойного угла равен разности единицы и удвоенного квадрата синуса данного угла.
Косинус двойного угла равен разности удвоенного квадрата косинуса данного угла и единицы.
В формуле sin (a + b ) = sin a · cos b + cos a · sin b примем a = b .
sin (a + a ) = sin a · cos a + cos a · sin a = 2 · sin a · cos a
sin 2a = 2sin a cos a , a -данный угол
Синус двойного угла равен удвоенному произведению синуса и косинуса данного угла.
Пример: Вычислить а) 2 sin 15° · cos 15°; б) cos 2 
- sin 2 .
Решение:
а) Воспользуемся формулой синуса двойного угла: sin 2a = 2 sin a · cos a
2 sin 15° · cos 15° = sin (2 · 15°) = sin 30° = 0,5 ;
б) Воспользуемся формулой косинуса двойного угла: cos 2a = cos 2 a - sin 2 a
cos 2 - sin 2 = cos (2 · ) = cos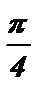 
= 
.
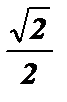Ответ: а) 2 sin 15° · cos 15° = 0,5 ; б) cos 2 - sin 2 = .
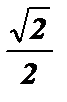В формуле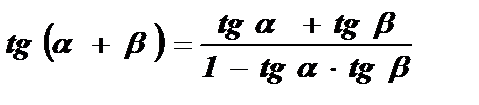 
примем a = b .
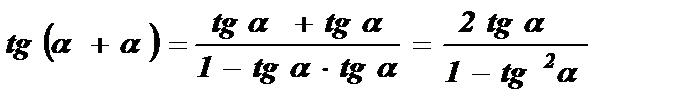
В формуле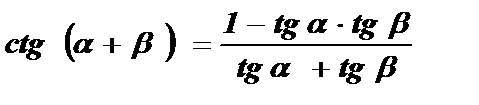 
примем a = b .
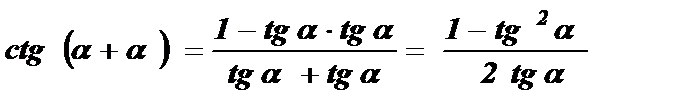
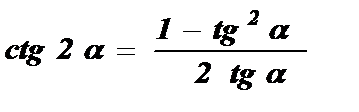
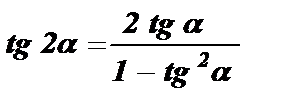
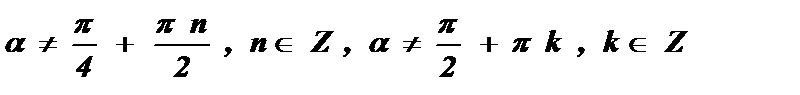
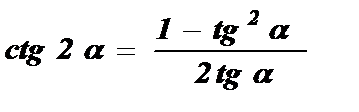
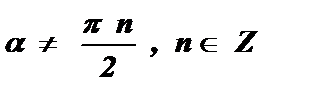
Тангенс двойного угла равен отношению удвоенного тангенса данного угла к разности единицы и квадрата тангенса данного угла.
Котангенс двойного угла равен отношению разности единицы и квадрата тангенса данного угла к удвоенному тангенсу данного угла.
Пример: Представить тригонометрические функции данного аргумента через тригонометрические функции вдвое меньшего аргумента:
sin a ; sin 5a ; cos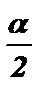 
; tg 42°.
Решение: Воспользуемся формулами синуса, косинуса и тангенса двойного угла:
sin a = sin (2 · 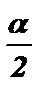) = 2 · sin 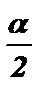· cos ;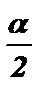
sin 5a = sin (2 ·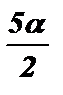 
) = 2 · sin 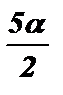· cos ;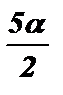
cos 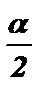= cos (2 · 
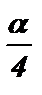) = cos 2 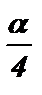- sin 2 ;
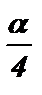tg 42° = tg (2 · 21° ) =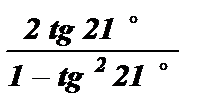 
Ответ: sin a = 2 · sin 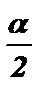· cos 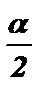; sin 5a = 2 · sin 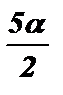· cos ;
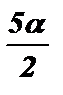cos 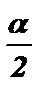= cos 2 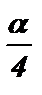- sin 2 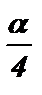; tg 42° =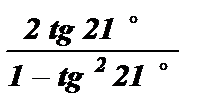
Из формулы cos 2a = 1 - 2 sin 2 a выразим sin 2 a через cos 2a .
Из формулы cos 2a = 2 cos 2 a -1 выразим cos 2 a через cos 2a .
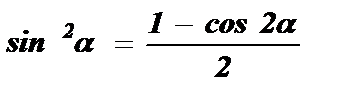или 2 sin 2 a = 1 - cos 2a
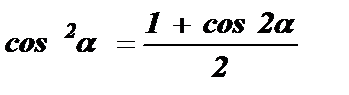или 2 cos 2 a = 1 + cos 2a
Замечание: Эти формулы называются формулами понижения степени.
Пример: Понизить степень выражения: 2 cos 2 3b ; 2 sin 2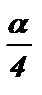 
Решение: Воспользуемся формулами понижения степени:
2 cos 2 3b = 1 + cos (2 · 3b ) = 1 + cos 6b
2 sin 2 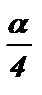= 1 - cos 
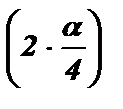= 1 - cos 
Ответ: 2 cos 2 3b = 1 + cos 6b ; 2 sin 2 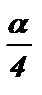= 1 - cos
Пример:
№1. Сократить дробь 
.
Решение: Разложим cos 80 º по формуле косинуса двойного угла и применим формулу сокращенного умножения a 2 – b 2 = (a – b) · (a + b) :
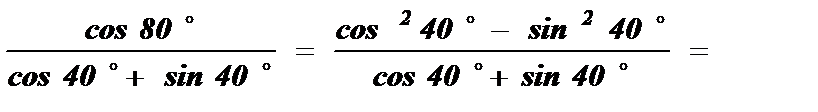
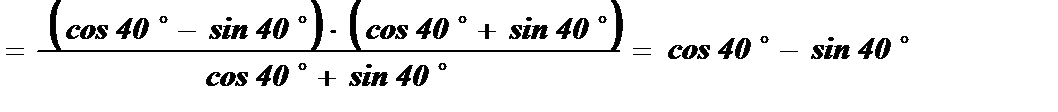
Ответ: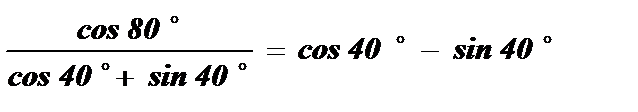 
№3. Доказать тождество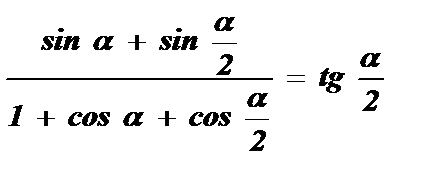 
.
Решение: В числителе дроби преобразуем sin a по формуле синуса двойного угла , а в знаменателе дроби применим формулу понижения степени:
sin a = 2 · sin 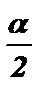· cos 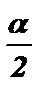; 2 cos 2 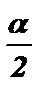= 1 + cos a .
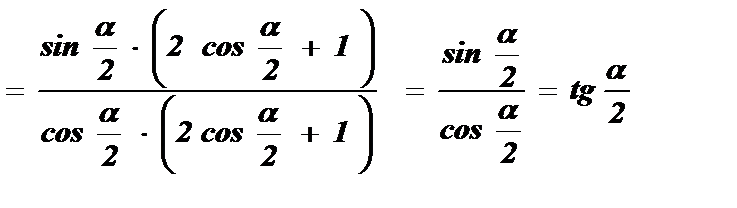
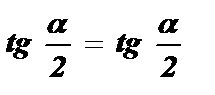
Определим область допустимых значений аргумента a :
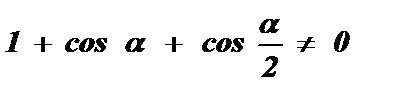или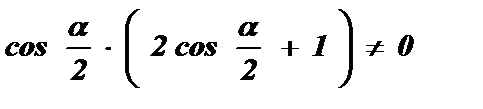 
; 
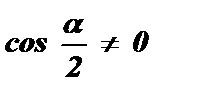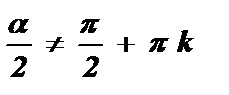; a ¹ p + 2p k , k Î Z ;
; 
; 
; 
.
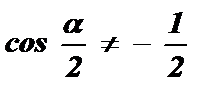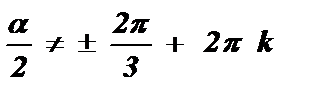ОДЗ : a ¹ p + 2p k , , k Î Z .
Упражнения:
№1. Представить тригонометрические функции данного аргумента через тригонометрические функции вдвое меньшего аргумента:
1) sin 4b ; 2) cos 8a ; 3) sin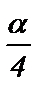 
; 4) cos 
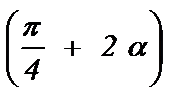; 5) tg 
.
№2. Представить тригонометрические функции данного аргумента через тригонометрические функции вдвое большего аргумента:
1) cos 2 15° ; 2) sin 2 1,5 p ; 3) sin 2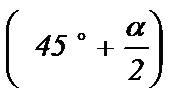 
; 4) cos 2 
.
№3. Упростить выражение:
а) 1 + cos 2a - 2 sin 2 a ; б)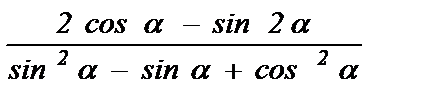 
;
в)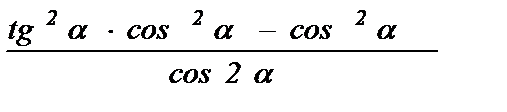 
.
№4. Доказать тождество:
а) (sin a + cos a) 2 – 1 = sin 2a ; в) 4 · sin a · cos a · cos 2a = sin 4a ;
б) cos 4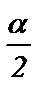 
- sin 4 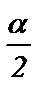= cos a ; г) 
.
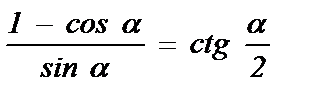№5. Вычислить sin 2a , cos 2a , tg 2a , если tg a =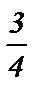 
и 180° < a < 270°.
12. Формулы приведения.
Определение: Формулы, выражающие тригонометрические функции от аргументов - a, 
, 
, 
, 
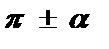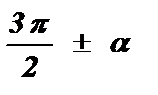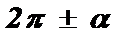, через тригонометрические функции от аргумента a , называются формулами приведения .
Замечание: Формулы приведения с аргументами - a , 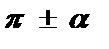, 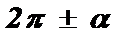называются формулами приведения горизонтального диаметра.
Формулы приведения с аргументами , 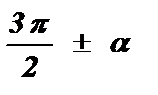называются формулами приведения вертикального диаметра.
| 2p + a |
| х |
| у |
| p + a |
|
|
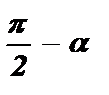
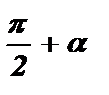
| p - a |
| 2p - a |
|
|
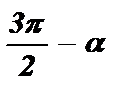
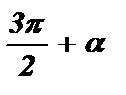
На рисунке показана принадлежность координатным четвертям углов:
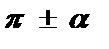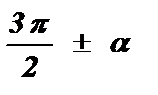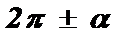, , , , где a – острый угол.
Правило: Если аргумент приводимой функции имеет вид - a , p ± a , 2p ±a , то название приводимой функции не меняется, а знак в правой части формулы ставится в зависимости от того, какой знак имела бы приводимая функция в случае, если 0 < a <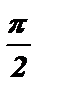 
.
Правило: Если аргумент приводимой функции имеет вид , 
, то название приводимой функции меняется (синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс), а знак в правой части формулы ставится в зависимости от того, какой знак имела бы приводимая функция в случае, если 0 < a < .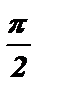
Пример:
№1. Упростить выражение: а) sin ( – p – a ); б) cos ( – 2p + a );
в) tg (–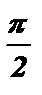 
+ a ); г) ctg ( – 
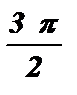– a ) .
Решение: Воспользуемся четностью, нечетностью тригонометрических функций и формулами приведения:
а) sin ( – p – a ) = sin (– ( p + a )) = – sin (p + a ) = – (– sina ) = sin a ;
б) cos ( – 2p + a ) = cos (– ( 2p – a )) = cos ( 2p – a ) = cos a ;
в) tg ( – 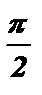+ a ) = tg (– ( 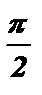– a )) = – tg ( 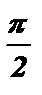– a ) = – ctga ;
г) ctg (– 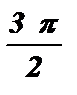– a )= ctg (– ( 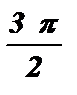+ a )) = – ctg ( 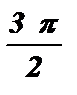+ a ) = – (– tga ) = tg a .
Ответ: а) sin ( – p – a ) = sin a ; б) cos ( – 2p + a ) = cos a ;
в) tg ( – 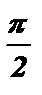+ a ) = – ctga ; г) ctg ( – 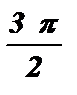– a ) = tg a .
№2. Вычислить: 1) sin 240° ; 2) cos ( – 315°); 3) tg ( – 225° ); 4) ctg 300°;
5) sin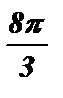 
; 6) cos 
.
Решение: Воспользуемся четностью, нечетностью тригонометрических функций и формулами приведения:
1) sin 240° = sin ( 180° + 60°) = –sin 60° = 
;
2) cos ( – 315°) = cos 315° = cos (270° + 45°) = sin 45° =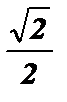 
;
3) tg ( – 225° ) = – tg 225° = – tg ( 180° + 45°) = – tg 45° = –1 ;
4) ctg 300° = ctg ( 360° – 60°) = – ctg 60° =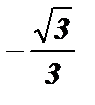 
;
5) 
;
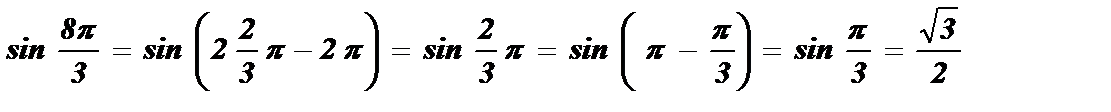6) 
.
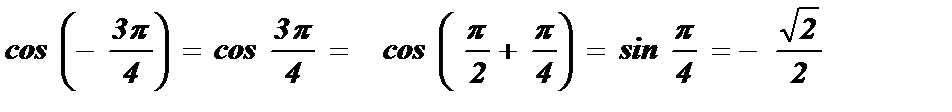Ответ: 1) sin 240° = ; 2) cos ( – 315°) = 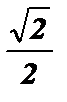; 3) tg ( – 225° ) = –1 ;
4) ctg 300° = 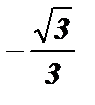; 5) 
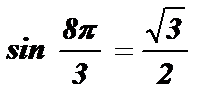; 6)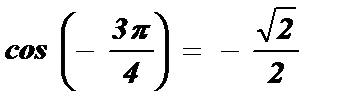 
№3. Доказать тождество:
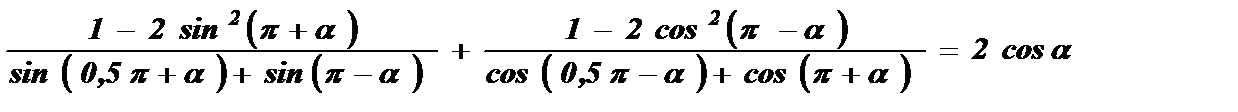
Решение: Воспользуемся формулами приведения и упростим аргументы тригонометрических функций:
sin (p + a) = – sina cos (p –a) = – cosa
sin (0,5 p + a) = cos a cos (0,5 p –a) = sina
sin (p –a) = sina cos (p + a) = – cosa
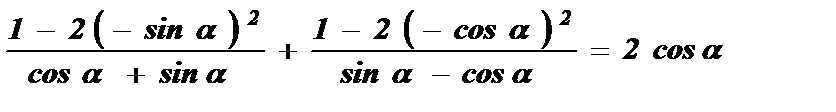
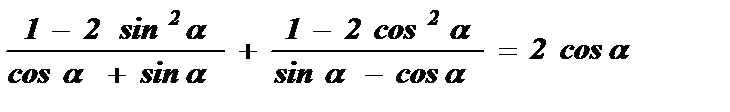
Воспользуемся формулой
cos 2a = cos 2 a - sin 2 a = 1 - 2 sin 2 a = 2 cos 2 a -1 :
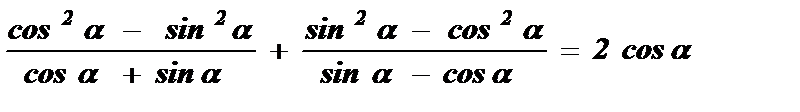
Воспользуемся формулой a 2 – b 2 = ( a – b ) · ( a + b ) :
Сократим дроби и приведем подобные слагаемые:
cos a – sina + sin a + cos a = 2 cos a 2 cos a = 2 cos a
Определим область допустимых значений выражения:
sin (0,5 p + a) + sin (p –a) ¹ 0 cos (0,5 p –a) + cos (p + a) ¹ 0
cos a + sin a ¹ 0 sin a – cosa ¹ 0
cos a ¹ – sina sin a ¹ cosa
a ¹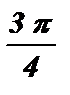 
+ pk , k Î Z a ¹ 
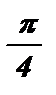+ pk , k Î Z
Область допустимых значений выражения: a ¹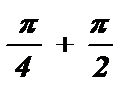 
k , k Î Z .
Ответ: Тождество верно при a ¹ 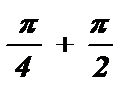k , k Î Z .
Упражнения:
№1. Привести к тригонометрической функции острого угла, сохраняя название функции: а) sin 173°; б) tg 355°; в) ctg (– 215°).
№2. Привести к тригонометрической функции острого угла, изменив название функции: а) sin 1140°; б) tg 440°; в) cos 400°
№3. Упростить выражение:
а) sin (a–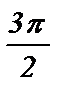 
) · cos ( p – a ) + sin (a – p ) · sin ( p + a ) ;
б) sin 2 (180° – a ) + sin 2 (270° – a );
в) cos 2 ( p + a ) + cos 2 (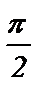 
+ a ) ;
г)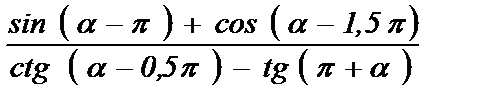 
;
д) 
;
е) sin 2 ( p – a ) + tg 2 ( p – a ) · tg 2 ( 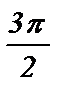+ a ) + sin ( 
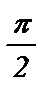+ a ) · cos (a – 2p) ;
ж) 
№4. Доказать тождество:
1) ( sin a + sin ( 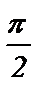– a )) 2 + ( cos a – cos ( 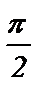– a )) 2 = 2 ;
2) 
;
3) 
;
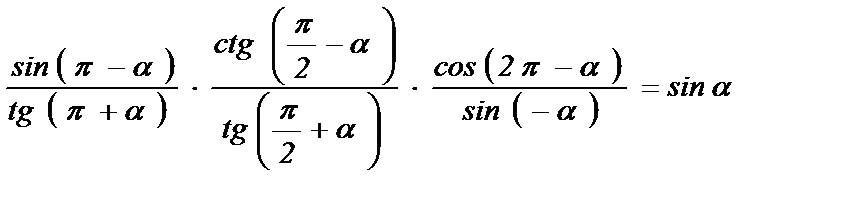4) sin ( 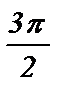+ a ) · ctg ( 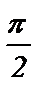– a ) + sin ( p – a ) + ctg ( 
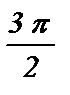– a ) = tg a ;
5) sin 200° · sin 310° + cos 340° · cos 50° =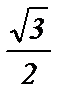 
№5. Вычислить:
1) tg 1800° – sin 495° + cos 480° ; 2) cos 4455°– cos (– 945°) + tg 1035°– сtg (– 1500°);
3) 
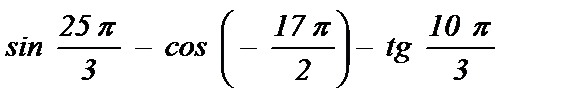; 4)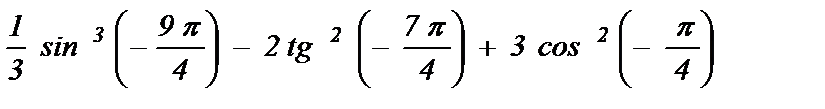 
13. Сумма и разность тригонометрических функций.
sin х + sin у = 2 · sin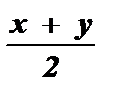 
· cos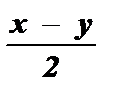 
Дата добавления: 2016-11-22; просмотров: 1759;