Построение краткой таблицы смертности
Идея и метод построения краткой таблицы смертности аналогичны только что рассмотренным для полных таблиц смертности. Разница только в длине возрастного интервала. Длина типичного i-того интервала возраста (хi, xi+l) в кратких таблицах равна ni = xi+1 - xi, т.е. превышает 1 год. Чаще всего она равна 5 годам. Существенным элементом здесь является средняя доля этого интервала, прожитая теми, кто умер в этом возрастном интервале.
Эта доля, обозначаемая аi,является обобщением рассмотренной выше доли а'х последнего года жизни. Определение этой доли является отдельной задачей, которая может решаться по-разному. Одно из возможных решений приведено во вставке на этой странице. В целом, к счастью, за исключением самых молодых возрастов, выбор величины ai не является критичным для построения кратких таблиц смертности. Обычно конвенционально принимается, что a0 = 0,1 для стран с низкой смертноcтью и 0,3 - для стран с высокой смертностью. Все прочие значения этого параметра принимаются равными 0,4 для всех остальных возрастных интервалов7.
Вместе с тем, как показал Чин Лонг Чань8, величина ai не зависит от конкретных значений коэффициента смертности в год, для которого рассчитывается краткая таблица смертности, а определяется лишь тенденцией изменения вероятности смерти внутри возрастного интервала (хi, xi+l) и может быть рассчитана на основании данных об одногодичных вероятностях смерти. Наличие специальных компьютерных программ построения таблиц смертности делает расчет этого параметра тривиальной задачей.
...Задача построения всех функций таблицы смертности по возрастным коэффициентам смертности jn (x), которые считаются равными табличным, на практике очень важна. Для ее решения надо решить специальное уравнение 1(х+п) - 1(х) - = -nm(х)nLp которое называется основным уравнением таблицы смертности. Существуют различные методы решения этого уравнения. Мы укажем простейший. На основе равенства (6.1) получим рас-
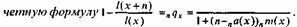
по которой числа доживающих легко восстанавливаются. Достаточно лишь знать па(х). Обычно полагают па(х) - 1/2 п, как это сделано в первых советских таблицах смертности... Валентей Д,И,, КвашаА.Я. Основы демографии. М., 1989. С. 119-120.
Формула для вероятности умереть на возрастном интервале (xj, xi+1) лет аналогична формуле для полных таблиц смертности и имеет следующий вид:
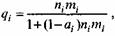
Эта формула построена при предположении, что внутри возрастного интервала (х + п) вероятность смерти или постоянна, или меняется линейно (в возрастных интервалах 0-1 год и 1- 4 года). Если же гипотеза линейности не принимается, то используют альтернативную формулу Гомперца (1825) и Фарра (1864):
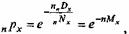
в которой гипотеза линейности заменяется гипотезой экспоненциального изменения вероятности смерти на возрастном интервале (х + п) лет. Соответственно, nqx = 1 - nрх.
Для возрастного интервала 0 - 1 год как альтернатива иногда просто приравнивают q0 к коэффициенту младенческой смертности.
Все прочие функции краткой таблицы смертности рассчитываются исходя из вычисленных ai , qi и корня таблицы l0.
Числа умирающих (di) на возрастном интервале (xi, xi + l) лет из числа доживающих до точного возраста xi + 1 лет рассчитываются по формулам:
di = l iqi; и li+1 = li - di , где i=0, 1 , 2, 3 - 1 .
Число человеко-лет, прожитых на возрастном интервале (xi , xi+l) лет, или число живущих на этом интервале, при принятии гипотезы линейности равно: Li = ni(li - di) + ai ni di , где i= 0,1,2, 3 - 1. Если же принимается экспоненциальная гипотеза, то для возрастного интервала 0 - 1 год используется альтернативная формула:
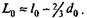
И для возрастного интервала 1 - 4 года:
4 l1 = 1,704 li + 2,533 l5 -237 l10.
Для последнего открытого возрастного интервала со эта величина равна:
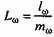
, где тw - повозрастный коэффициент смертности.
Покажем на примере данных о повозрастной смертности мужчин в России в 1997 г, процедуру расчета краткой таблицы смертности мужского населения (табл. 6.5). Примем при этом гипотезу линейности, а также значения параметра аi, равные его величинам по таблице смертности для всего населения США 1960 г., поскольку тогдашний уровень смертности в этой стране довольно близок нынешнему ее уровню в России. Средняя ожидаемая продолжительность жизни для обоих полов в 1960 г. в США равнялась примерно 70 годам, а уровень младенческой смертности - 26,8%о9.
В России средняя ожидаемая продолжительность жизни для обоих полов в 1997 г. была равна примерно 67 годам, а уровень младенческой смертности-17,2%о.
Рассчитаем краткую таблицу смертности с помощью нижеследующей пошаговой процедуры.
· Шаг 1. Рассчитываем длину возрастного интервала (xi , xi+1), Для интервала 0-1 год она равна 1 году; для интервала 1-4 года она равна 4 годам; для всех прочих - 5 годам. Эту же величину (5 лет) мы условно принимаем и для последнего открытого интервала 85 лет и старше. Хотя знание точного возраста смерти в самых старших возрастах позволяет более точно оценить его длину. Однако для описываемой процедуры длина открытого интервала не играет никакой роли.
· Шаг 2. Переводим значения повозрастных коэффициентов смертности из промилле в относительные доли единицы.
· Шаг 3. Учитывая величину параметра аi , определяем qi - вероятность умереть на возрастном интервале (хi , xi+l). При этом для интервала 0-1 год принимаем значение q0 , равное коэффициенту младенческой смертности.
· Шаг 4. С помощью итеративного процесса рассчитываем числа умирающих (di) на возрастном интервале (xi , xi+l) и числа доживающих (li) до точного возраста х лет. При этом l0 принимаем равным 10 000 (учитывая точность повозрастных коэффициентов смертности); d0 = lOq0 и 11 = l0 - d0 . Затем вся процедура повторяется для каждого возрастного интервала (xi , xi+l), кроме последнего открытого интервала 85 лет и старше. На этом интервале вероятность смерти равна единице, поэтому d18 = l18.
· Шаг 5. Рассчитываем по приведенным выше формулам числа живущих (Li) на возрастном интервале (xi , xi+1). Для последнего открытого возрастного интервала 85 лет и старше эта величина равна: L18 = l18/m18 , где m18 - повозрастной коэффициент смертности для этого возрастного интервала.
· Шаг 6. Рассчитываем общее число человеко-лет, которое предстоит прожить дожившим до начала возрастного интервала (xi , xi+1) лет (до точного возраста х лет). Эта величина равна сумме всех Li от i до w (в данном случае до 18).
· Шаг 7. Разделив Li на li , получим среднюю ожидаемую продолжительность предстоящей жизни для дожившего до начала возрастного интервала (xi ,xi+1) лет (до точного возраста х лет), еi .Построение краткой таблицы смертности закончено.
В предпоследней колонке таблицы приведены официальные данные о величине ei , опубликованные в Демографическом ежегоднике РФ 98, а в последней - разность значений этого показателя, рассчитанных нами, и официальных. Как видно, они близки друг к другу, хотя наш расчет показал несколько большие, чем официальные, значения средней ожидаемой продолжительности жизни для возрастов от 0 до 59 лет. Для старших же возрастов, напротив, расчетные значения меньше официальных. Полного совпадения не может быть, поскольку официальные данные рассчитываются по полным таблицам смертности.
В современных условиях расчет таблиц смертности, как кратких, так и полных, значительно упростился и стал гораздо менее трудоемким, чем ранее. Разработаны специальные пакеты программ и электронные таблицы, позволяющие все процедуру расчета таблиц смертности свести к простому вводу ее повозрастных коэффициентов и некоторых других параметров. Примером таких пакетов является Mort-Pak, примером электронных таблиц - LTPOPDTH и LTMXQXAD из комплекта PAS1.
Дата добавления: 2016-11-22; просмотров: 782;
