Лекция 6. Игровые модели при оценке риска в условиях неопределенности внешней среды. Метод дерева решений.

В большинстве случаев для принятия управленческих решений используется неполная и неточная информация, которая и образует ситуацию неопределенности. Для обоснования решений в условиях неопределенности используют:

1) методы теории статистических решений (игры с природой);

2) методы теории игр.

Организации обычно имеют цели, которые противоречат целям других организаций-конкурентов. Поэтому работа менеджеров часто заключается в выборе решения с учетом действий конкурентов. Для решения таких проблем предназначены методы теории игр.

Теория игр - это раздел прикладной математики, изучающий модели и методы принятия оптимальных решений в условиях неопределенности, конфликтности, т.е. в ситуациях, когда интересы сторон (игроков) либо противоположны, либо не совпадают, хотя и не являются противоположными.

Конфликтными считают такие ситуации, в которых сталкиваются интересы двух или более сторон, преследующих различные (чаще противоречивые) цели. При этом каждое решение должно приниматься в расчете на умного противника, который пытается не позволить другому участнику игры достичь успеха.

С целью исследования конфликтной ситуации строят ее формализованную упрощенную модель. Чтобы построить такую ​​модель, необходимо четко описать конфликт, то есть:

1) уточнить количество участников (участники или стороны конфликта называются игроками);

2) указать на все возможные способы (правила) действий для игроков, которые называются стратегиями игроков;

3) рассчитать, какими будут результаты игры, если каждый игрок выберет определенную стратегию (т.е. выяснить выигрыши или проигрыши игроков).

Основную задачу теории игр можно сформулировать так: определить, какую стратегию должен применить умный игрок в конфликте с умным противником, чтобы гарантировать каждому из них выигрыш, притом так, что отклонение любого из игроков от оптимальной стратегии может только уменьшить его выигрыш.

Участниками игры (игроками) могут быть отдельные лица, предпринимательские структуры, а также различные явления природы и внешняя среда (экономика).

Центральное место в теории игр занимают парные игры с нулевой суммой, т.е. игры, в которых;

- Участвуют только две стороны;

- Одна сторона выиграет ровно столько, сколько проигрывает другая.

Такой равновесный выигрыш, на который имеют право рассчитать обе стороны, если они будут придерживаться своих оптимальных стратегий, называется ценой игры. Решить парную игру с нулевой суммой означает найти пару оптимальных стратегий (одну для первого игрока, а вторую - для второго) и цену игры.

Нижняя цена игры (которая принята обозначать α) рассчитывается путем определения минимального значения Аij по каждой строке платежной матрицы (стратегии игрока Y) и выбора из них максимального значения, т.е.:

α = max (min Aij) – для прибыли

Верхняя цена игры (которая принята обозначать β) рассчитывается путем определения максимального значения Аij за каждым столбцом платежной матрицы (стратегии игрока Z) и выбора из них минимального значения, т.е.:

β = min (max Aij)

Если нижняя цена игры равняется верхний (α = β), то такая игра имеет седловую точку и решается в чистых стратегиях. Седловая точка - это такой элемент в платежной матрицы игры, который является минимальным в своей строке и одновременно максимальным в своем столбце.

Чистые стратегии - это пара стратегий (одна - для первого игрока, а вторая - для второго игрока), которые перекрещиваются в седловой точке. Седловая точка в этом случае и определяет цену игры.

Игры, которые не имеют седловой точки, на практике встречаются чаще. Доказано, что и в этом случае решение всегда есть, но оно находится в пределах смешанных стратегий. Найти решение игры без седловой точки означает определение такой стратегии, которая предусматривает использование нескольких чистых стратегий.

В играх с седловой точкой отклонения одного игрока от своей оптимальной стратегии уменьшает его выигрыш (в лучшем случае выигрыш остается неизменным). В играх, которые не имеют седловой точки, ситуация иная. Отходя от своей оптимальной стратегии, игрок имеет возможность получить больший выигрыш за нижнюю цену игры. Но такая попытка связана с риском: если второй игрок угадает, какую стратегию применил первый, тогда он также отступит от своей минимакснои стратегии. В результате выигрыш первого игрока будет меньше нижней цены игры. Единственная возможность помешать противнику угадать, какая стратегия используется - это применить несколько чистых стратегий. Отсюда появляется понятие "смешанная стратегия".

Статистические игры образуют отдельный класс матричных игр, в которых одним из участников является человек или группа людей, объединенных общей целью, а другим - внешняя среда (игрок А - «статистик», игрок Б - «природа»). Термином «природа» обозначается весь комплекс внешних условий, при которых статистик вынужден принимать решения. «Природа» (экономика) безразлична к выигрышу и не стремится использовать в свою пользу погрешности «статистика».

Дерево решений

Дерево решений представляет собой модель, которая позволяет разбить большую и сложную проблему принятия решения в условиях риска на совокупность меньших проблем, которые могут быть рассмотрены от­дельно, а затем в совокупности. Таким образом можно решить общую про­блему. Особенно полезным построение дерева решений оказывается, ког­да сложная ситуация может быть разбита на последовательность более простых проблем, которые выстроены в естественном порядке. Дерево решений применяется при решении сложных многоэтапных вероятно­стных проблем. Большинство управленческих решений, принимаемых в ходе управления проектом, имеет именно такую природу.

На дереве решений каждая ветвь, представляющая собой либо существу­ющий вариант действий, либо возможное последствие выбранного дей­ствия, делится в определенных точках на совокупность других ветвей. Такие точки бывают двух видов:

точки принятия решения, в которых возникает несколько вари­антов действий;

точки возникновения последствий, в которых появляется несколь­ко возможных последствий выбранных действий.

Рис. 1. Общий вид дерева решений

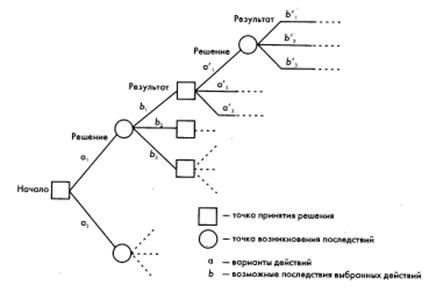
Обычно точки принятия решения обозначают в виде квадратов, а точки возникновения последствий — в виде кругов. Количество точек принятия решения и точек возникновения последствий может быть каким угодно, а значит, различных ветвей на дереве принятия решений может быть сколь угодное множество. При этом они могут иметь неодинаковое количество точек принятия решения и возникновения последствий. Каждая ветвь, исходящая из точки принятия решения, представляет собой возможный вариант действий и обычно обозначается символьно (см. рис. 1) и опи­сывается несколькими словами, лаконично характеризующими суть воз­можного действия. Далее ветвь возможного варианта действия, проходя через точку возникновения последствий, разбивается на несколько резуль­татов действий, которые также имеют символьное обозначение и краткое словесное описание. Самое важное, что каждое последствие имеет свою оценку вероятности, а также количественную оценку результата, как пра­вило, денежную. При анализе проблемы, по которой принимается реше­ние (в отношении проекта в целом или отдельной его части), путем прямо­го хода (слева направо) осуществляется структуризация проблемы, т.е. разбиение ее на совокупность логически связанных вариантов реше­ний и их последствий, а также присвоение им вероятностных и количе­ственных результатов. Структурировав проблему прямым ходом, ее под­вергают анализу обратным ходом (справа налево) и оценивают существу­ющие варианты решений на основе ожидаемой денежной стоимости (Expected Monetary Value — EMV). Этот показатель рассчитывается как сумма произведений вероятности и количественной (денежной) оценки по каждому из возможных последствий.

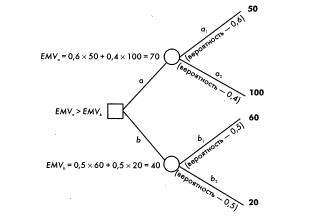
К примеру, существует альтернатива двух решений а и b. Решение а имеет последствия а₁ и а₂, вероятность наступления которых равна 0,6 и 0,4 со­ответственно, а количественная оценка результата — 50 и 100 соответ­ственно. Решение b имеет последствия b₁ и b₂, вероятность наступления которых равна 0,5 и 0,5 соответственно, а количественная оценка резуль­тата — 60 и 20 соответственно. Тогда ожидаемая денежная оценка реше­ния а будет равна 70 (0,6 х 50 4- 0,4 х 100), а тот же показатель для решения b — 40 (0,5 х 60 4- 0,5 х 20). Таким образом, решение а является более предпочтительным на основе того, что его ожидаемая денежная оценка больше, чем у альтернативы b.

Рис. 2. Анализ и выбор с помощью дерева решений