Входное сопротивление линии

Входное сопротивление линии определяется отношением напряжения и тока в начале линии. Найдем выражение входного сопротивления

Z_вх(jω) = Ú₁/Ì_1,

используя уравнения (6.11)

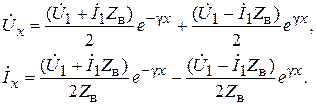
Если учесть, что 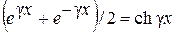и и 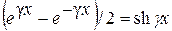принять при x = l Ú_x = Ú_н и Ì_x = Ì_н, то система уравнений (6.11) примет вид

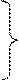
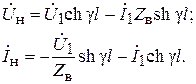(6.28)

Разрешая эту систему уравнений относительно напряжения Ú₁ и тока Ì₁, получим

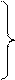
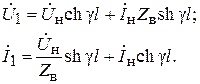(6.29)

Используя уравнения (6.29), получим выражение входного сопротивления

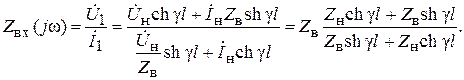(6.30)

Рассмотрим некоторые частные режимы работы линии.

1. При согласованном включении линии (Z_н = Z_в) из (6.30) получим, что

Z_нх = Z_в.

2. Если выходные зажимы линии замкнуты накоротко (Z_н = 0), то формула (6.30) упрощается:

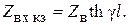(6.31)

3. В случае разомкнутых выходных зажимов (Z_н = ∞)

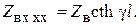(6.32)

4. Когда линия нагружена на произвольное сопротивление, не равное волновому (Z_н ≠ Z_в), можно пользоваться для расчетов не только формулой (6.30), но и более удобной. Для этого разделим числитель и знаменатель в (6.30) на ch γl:

.

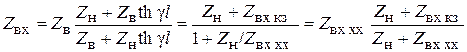Линия без потерь

Вторичные параметры и уравнения передачи. Реальная линия всегда обладает потерями. Однако в ряде случаев удобно считать линию идеальной, т. е. не имеющей потерь: R₁ = G₁ = 0. Такая идеализация оправдана для коротких по длине линий, работающих на сверхвысоких частотах (фидеров, элементов радиотехнических устройств, полосковых линий и др.), где выполняются условия R₁ << ωL и G₁ << ωC.

Коэффициент распространения линии без потерь

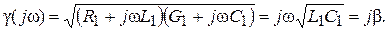
Отсюда коэффициент ослабления α = 0, а коэффициент фазы 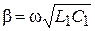линейно зависит от частоты.

Коэффициент фазы β связан с длиной волны электромагнитного колебания. Длиной волны λ называется расстояние между двумя точками, взятыми в направлении распространения волны, фазы в которых отличаются на 2π. Следовательно, βλ = 2π иλ = 2π / β.

Волновое сопротивление линии без потерь

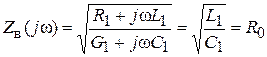
является чисто резистивным (активным).

Уравнения передачи линии без потерь получаются из (6.29), если учесть, что ch γl = ch jβl = cos βl и sh γl = sh jβl = jsin βl:

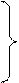
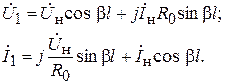(6.33)

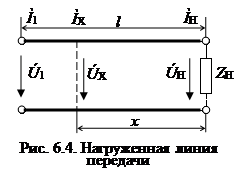При анализе процессов в линии без потерь общепринято расположение той или иной точки на линии характеризовать ее удаление не от начала линии, как это делали прежде, а от конца линии (от нагрузки) (рис. 6.4). В этом случае уравнения передачи линии без потерь, выражающие комплексные значения напряжения и тока в произвольной точке линии x, отсчитанной от ее конца, записываются в виде:

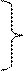
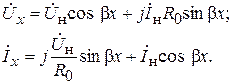(6.34)

Формула (6.30) входного сопротивления для линии без потерь примет следующий вид

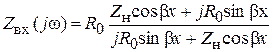. (6.35)