Метод экономического роста

Пусть уравнение цены равной себестоимости некоторой единицы продукции Х и средней прибыли имеет вид 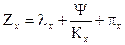. Следует полагать или утверждать, что есть альтернативный тип продукции Y с уравнением, которое имеет хотя бы одну общую точку К в уравнении Y вида 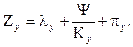Поэтому цены в точке К равны между собой. Приравняем их:

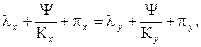
где p_х, p_y – средняя прибыль товаров х и у,

откуда общая точка Ψ будет равна

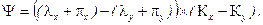
Прирост ΔК равен

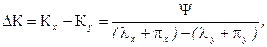
или

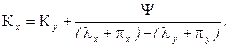
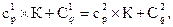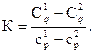Вариант 1.Если то Если вычесть
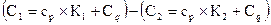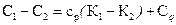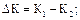
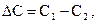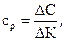из первого второе , то получим: , откуда или где
с_р – удельная себестоимость изделия, р.; С_q – косвенные расходы фирмы q.

Вариант 2. Если два уравнения объема реализации имеют совместное решение, т.е. равны: 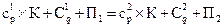, то 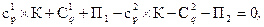откуда 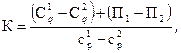где П₁, П₂ – валовая прибыль фирмы 1 или 2.

Вариант 3. Если уравнение цены представить в виде суммы средней себестоимости некоторой продукции Х и средней прибыли :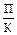

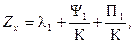
то следует полагать, что есть альтернативный тип продукции Y с уравнением, которое имеет хотя бы одну общую точку К в уравнении Y вида:

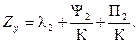
Цены в этой точке К равны между собой Z_х(К) = Z_у(К):

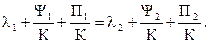
Умножим обе части равенства на К и, преобразовав их, получим:

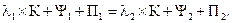
В результате получили два уравнения выручки от реализации, которые имеют единую общую точку К → К_e:

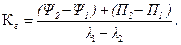
Пример 6.7

Определите К_e, если дана следующая информация (табл. 21).

Таблица 21