Теоретические модели в структуре теории
Своеобразной клеточкой организации теоретических знаний на каждом из его подуровней является двухслойная конструкция - теоретическая модель и формулируемый относительно нее теоретический закон.
Рассмотрим вначале, как устроены теоретические модели.
В качестве их элементов выступают абстрактные объекты (теоретические конструкты), которые находятся в строго определенных связях и отношениях друг с другом.
Теоретические законы непосредственно формулируются относительно абстрактных объектов теоретической модели. Они могут быть применены для описания реальных ситуаций опыта лишь в том случае, если модель обоснована в качестве выражения существенных связей действительности, проявляющихся в таких ситуациях.
Например, если изучаются механические колебания тел (маятник, тело на пружине и т.д.), то чтобы выявить закон их движения, вводят представление о материальной точке, которая периодически отклоняется от положения равновесия и вновь возвращается в это положение. Само это представление имеет смысл только тогда, когда зафиксирована система отсчета. А это - второй теоретический конструкт, фигурирующий в теории колебаний. Он соответствует идеализированному представлению физической лаборатории, снабженной часами и линейками. Наконец, для выявления закона колебаний необходим еще один абстрактный объект - квазиупругая сила, которая вводится по признаку: приводить в движение материальную точку, возвращая ее к положению равновесия.
Система перечисленных абстрактных объектов (материальная точка, система отсчета, квазиупругая сила) образуют модель малых колебаний (называемую в физике осциллятором). Исследуя свойства этой модели и выражая отношения образующих ее объектов на языке математики, получают формулу 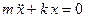 , которая является законом малых колебаний.
, которая является законом малых колебаний.
Этот закон непосредственно относится к теоретической модели, описывая связи и отношения образующих ее абстрактных объектов. Но поскольку модель может быть обоснована как выражение сущности реальных процессов колебания тел, постольку полученный закон можно применить ко всем подобным ситуациям.
В развитых в теоретическом отношении дисциплинах, применяющих количественные методы исследования (таких, как физика), законы теории формулируются на языке математики. Признаки абстрактных объектов, образующих теоретическую модель, выражаются в форме физических величин, а отношения между этими признаками - в форме связей между величинами, входящими в уравнения. Применяемые в теории математические формализмы получают свою интерпретацию благодаря их связям с теоретическими моделями. Богатство связей и отношений, заложенное в теоретической модели, может быть выявлено посредством движения в математическом аппарате теории. Решая уравнения и анализируя полученные результаты, исследователь как бы развертывает содержание теоретической модели и таким способом получает все новые и новые знания об исследуемой реальности.
Теоретические модели не являются чем-то внешним по отношению к теории. Они входят в ее состав. Их следует отличать от аналоговых моделей, которые служат средством построения теории, ее своеобразными строительными лесами, но целиком не включаются в созданную теорию. Например, аналоговые гидродинамические модели трубок с несжимаемой жидкостью, вихрей в упругой среде и т.д., применявшиеся при построении Максвеллом теории электромагнитного поля, были "строительными лесами", но модели, характеризующие процессы электромагнетизма как взаимосвязи электрических и магнитных полей в точке, зарядов и электрических токов в точке, - были составной частью теории Максвелла. Чтобы подчеркнуть особый статус теоретических моделей, относительно которых формулируются законы и которые обязательно входят в состав теории, назовем их теоретическими схемами. Они действительно являются схемами исследуемых в теории объектов и процессов, выражая их существенные связи.
Соответственно двум выделенным подуровням теоретического знания можно говорить о теоретических схемах в составе фундаментальной теории и в составе частных теорий.
В основании развитой теории можно выделить фундаментальную теоретическую схему, которая построена из небольшого набора базисных абстрактных объектов, конструктивно независимых друг от друга, и относительно которой формулируются фундаментальные теоретические законы.
Например, в ньютоновской механике ее основные законы формулируются относительно системы абстрактных объектов: "материальная точка", "сила", "инерциальная пространственно-временная система отсчета". Связи и отношения перечисленных объектов образуют теоретическую модель механического движения, изображающую механические процессы как перемещение материальной точки по континууму точек пространства инерциальной системы отсчета с течением времени и как изменение состояния движения материальной точки под действием силы.
Аналогичным образом в классической электродинамике сущность электромагнитных процессов представлена посредством теоретической модели, которая образована отношениями конструктов "электрическое поле в точке", "магнитное поле в точке" и "ток в точке". Выражением этих отношений являются фундаментальные законы теории электромагнитного поля.
Кроме фундаментальной теоретической схемы и фундаментальных законов в состав развитой теории входят частные теоретические схемы и законы.
В механике это - теоретические схемы и законы колебания, вращения тел, соударения упругих тел, движение тела в поле центральных сил и т.п.
В классической электродинамике к слою частных моделей и законов, включенных в состав теории, принадлежат теоретические схемы электростатики и магнитостатики, кулоновского взаимодействия зарядов, магнитного действия тока, электромагнитной индукции, постоянного тока и т.д.
Когда эти частные теоретические схемы включены в состав теории, они подчинены фундаментальной, но по отношению друг к другу могут иметь независимый статус. Образующие их абстрактные объекты специфичны. Они могут быть сконструированы на основе абстрактных объектов фундаментальной теоретической схемы и выступать как их своеобразная модификация. Различию между фундаментальной и частными теоретическими схемами в составе развитой теории соответствует различие между ее фундаментальными законами и их следствиями.
Как уже отмечалось, частные теоретические схемы и связанные с ними уравнения могут предшествовать развитой теории. Более того, когда возникают фундаментальные теории, рядом с ними могут существовать частные теоретические схемы, описывающие эту же область взаимодействия, но с позиций альтернативных представлений. Так, например, обстояло дело с фарадеевскими моделями электромагнитной и электростатической индукции. Они возникли в период, когда создавался первый вариант развитой теории электричества и магнетизма - электродинамика Ампера. Это была достаточно развитая математизированная теория, которая описывала и объясняла явления электричества и магнетизма с позиций принципа дальнодействия. Что же касается теоретических схем, предложенных Фарадеем, то они базировались на альтернативной идее - близкодействия.
Не лишне подчеркнуть, что законы электростатической и электромагнитной индукции были сформулированы Фарадеем в качественном виде, без применения математики. Их математическая формулировка была найдена позднее, когда была создана теория электромагнитного поля. При построении этой теории фарадеевские модели были видоизменены и включены в ее состав.
Это обстоятельство характерно для судеб любых частных теоретических схем, ассимилируемых развитой теорией. Они редко сохраняются в своем первоначальном виде, а чаще всего трансформируются и только благодаря этому становятся компонентом развитой теории.
Итак, строение развитой естественно-научной теории можно изобразить как сложную, иерархически организованную систему теоретических схем и законов, где теоретические схемы образуют своеобразный внутренний скелет теории.
Функционирование теорий предполагает их применение к объяснению и предсказанию опытных фактов. Чтобы применить к опыту фундаментальные законы развитой теории, из них нужно получить следствия, сопоставимые с результатами опыта. Вывод таких следствий характеризуется как развертывание теории.
Дата добавления: 2016-10-17; просмотров: 626;
